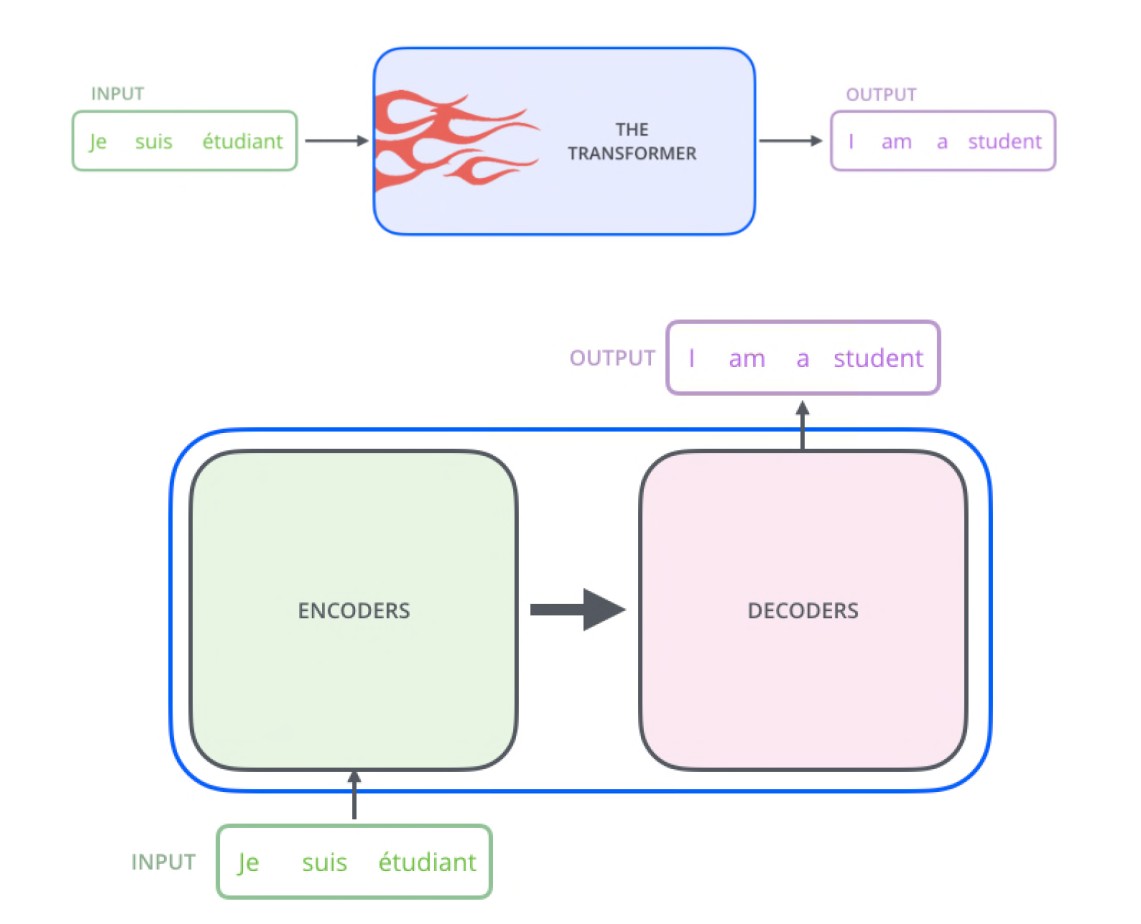
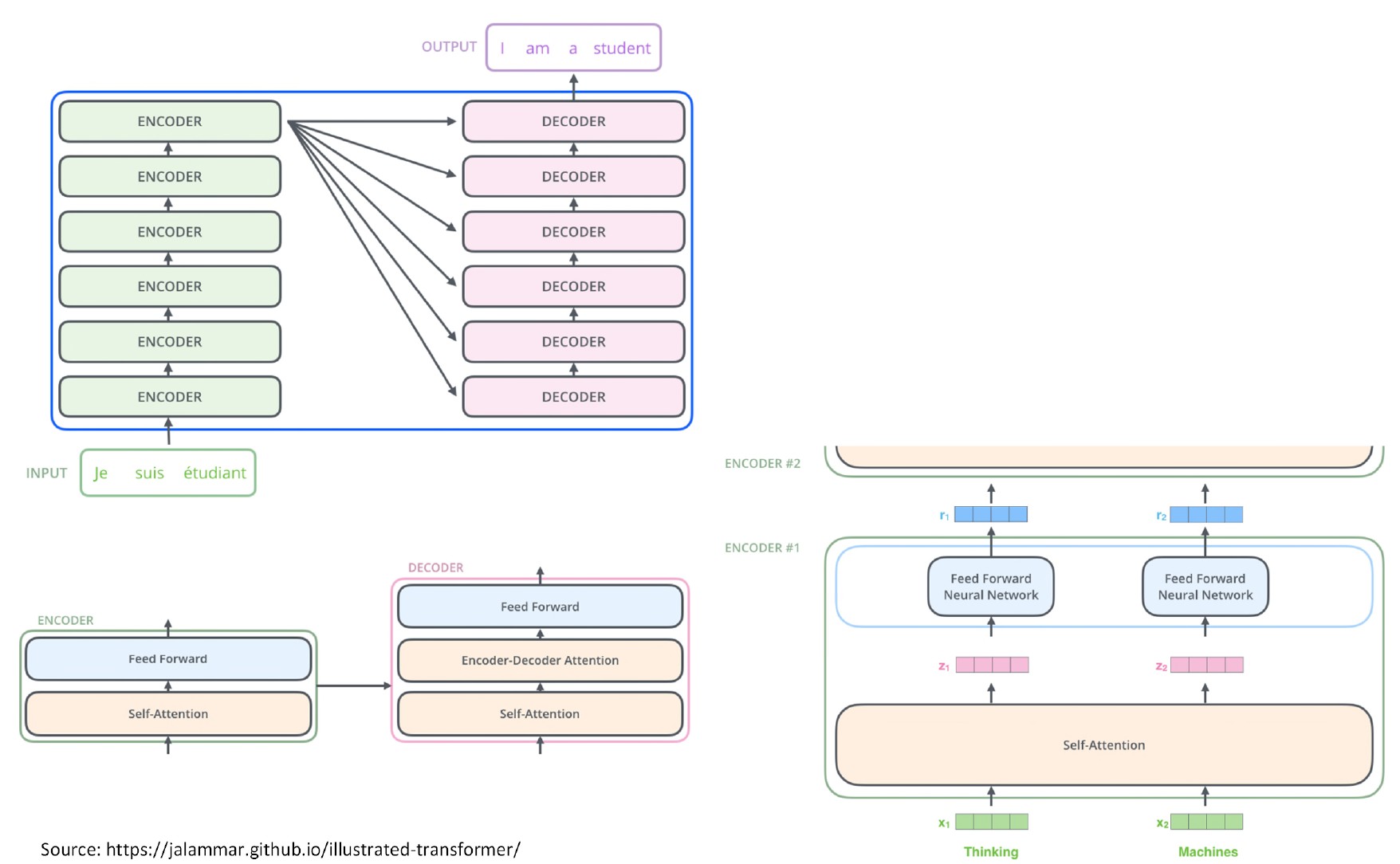
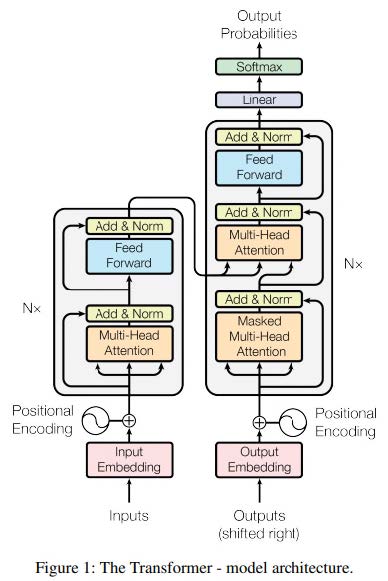
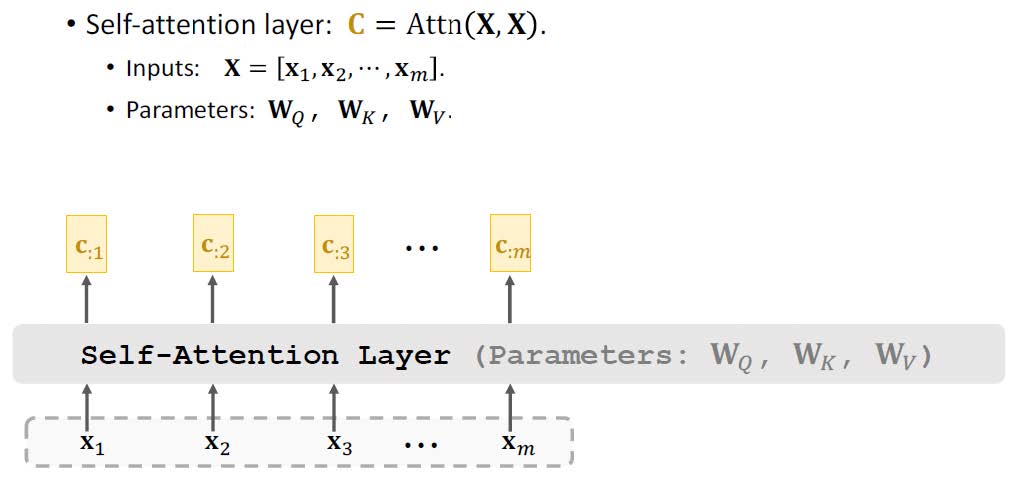
聚类分析

发表于 2024-11-08

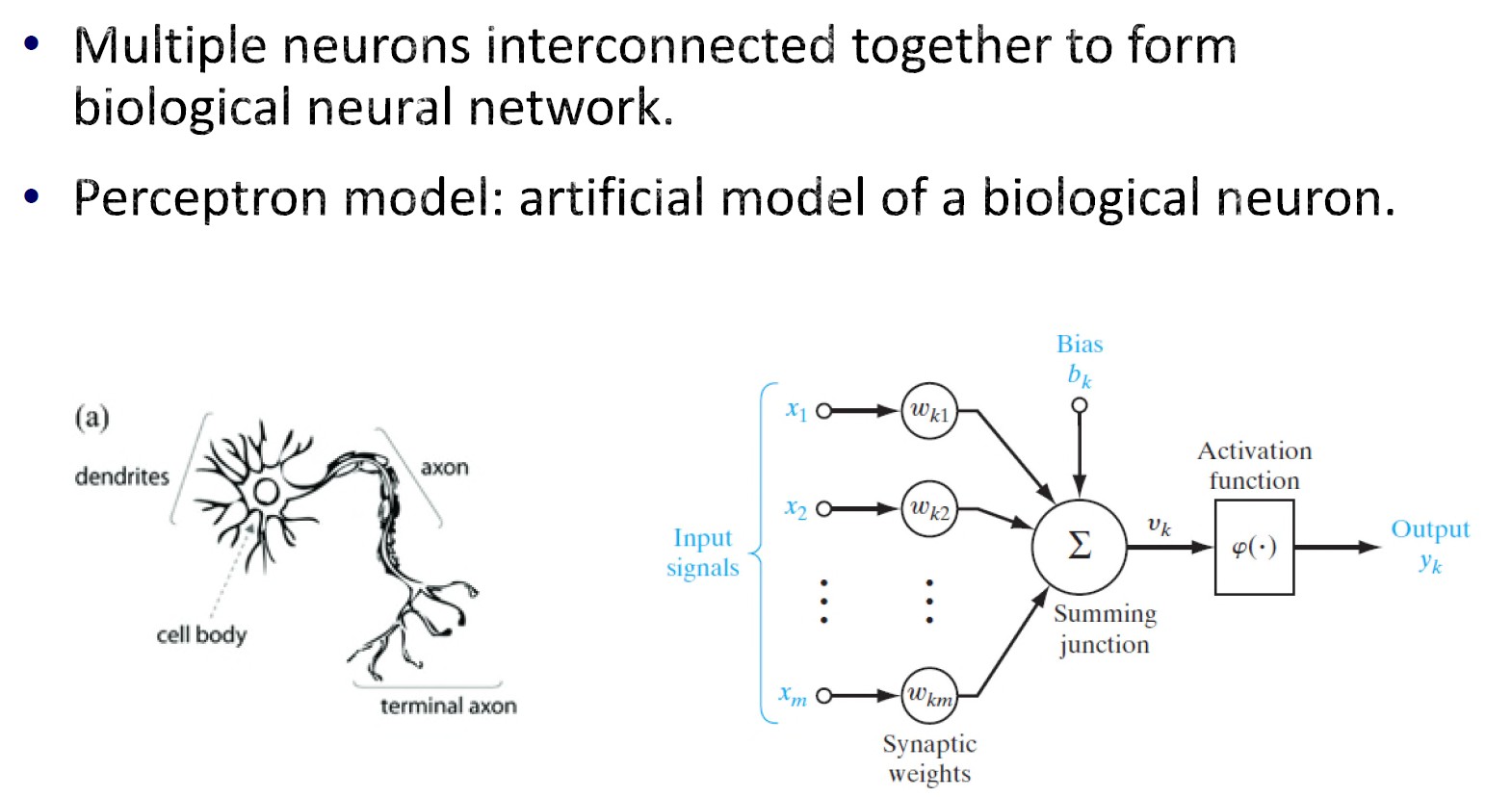
介绍

到目前为止，我们假设使用的训练样本是标记数据。使用标记数据的程序被称为监督学习。现在我们将探索使用未标记样本的无监督学习。

无监督学习不需要监督标记的训练数据集，因此它是一种理想的机器学习技术，可用于发现数据背后的模式和分组。无监督学习主要涉及两个主题：聚类分析和关联分析。本课程将重点介绍聚类分析，该分析已广泛应用于市场细分、搜索结果分组等。

聚类分析基础

粗略地说，聚类过程以具有很强内部相似性的数据点的聚类或分组的形式产生数据描述。正式的聚类过程使用标准函数并寻求优化标准函数的分组。

相似度测量

一旦我们将聚类问题描述为在一组数据中寻找自然分组的问题，我们就需要定义：

自然分组是什么意思？
在什么意义上，一个簇/组中的样本比其他簇中的样本更相似？

两个样本之间的相似性最明显的衡量标准是它们之间的距离。预计同一簇中的样本之间的距离明显小于不同簇中的样本之间的距离，如下所示。

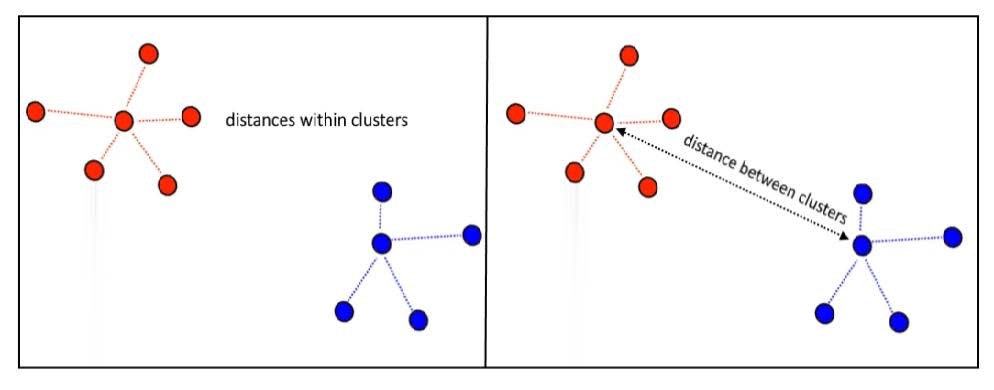
一大类距离度量具有以下形式：

\[ d(\mathbf x,\mathbf x')=\left(\sum_{i=1}^d\left\lvert x_i-x_i'\right\rvert^q\right)^\frac1q \]

其中\(q\geq1\)是可选参数。这种距离度量称为闵可夫斯基距离。

如果\(q=2\)，则距离度量是常用的欧几里得距离。

如果\(q=1\)，则距离度量称为曼哈顿或城市街区距离。

也可以使用一些其他距离度量，例如Mahalanobis距离和余弦相似度度量。

聚类算法的类型

聚类算法有多种类型，包括

基于质心的聚类（分区方法）
层次聚类
基于分布的聚类
基于密度的聚类

基于质心的聚类

基于质心的方法也称为分区方法。它是一种将数据划分为非层次组的聚类方法。分区聚类最常见的例子是 K-Means聚类算法。

层次聚类

层次聚类可以作为分区聚类的替代方案，因为不需要预先指定要创建的聚类数量。在此技术中，数据集被划分为聚类以创建树状结构，也称为树状图。

基于分布的聚类

在基于分布的聚类方法中，数据是根据数据集属于特定分布的概率进行划分的。分组是通过假设某些分布（例如高斯分布）来完成的。

此类型的例子是高斯混合模型（GMM）。

基于密度的聚类

基于密度的聚类方法将密度高的区域连接成簇，只要密集区域能够连接起来，就可以形成任意形状的分布。

该算法通过识别数据集中的不同聚类并将高密度区域连接成聚类来实现这一点。数据空间中的密集区域被稀疏区域相互划分。

如果数据集的密度各不相同且维度较高，算法在对数据点进行聚类时可能会遇到困难。

基于质心的聚类

基于质心的聚类被认为是最简单但最有效的聚类算法之一。基于质心的聚类背后的直觉是，一个聚类由一个中心向量来表征和表示，而靠近这些中心向量的数据点被分配到相应的聚类中。

k-Means聚类算法

K 均值聚类是最流行的基于质心的方法。

假设我们有一组\(n\)个样本，\(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n\)，我们希望将其划分为恰好\(k\)个不相交的子集\(D_1,D_2,\cdots,D_k\)。每个子集代表一个聚类，同一聚类中的样本在某种程度上比不同聚类中的样本更相似。

那么问题就是找到使标准函数极值的分区。接下来，我们研究标准函数的特征，然后研究如何找到最佳分区。

聚类内平方和标准 (WCSS)

K-Means聚类采用聚类内平方和 (WCSS) 作为标准。设\(n_i\)为\(D_i\)中的样本数，设\(\mathbf m_i\)为这些样本的平均值：

\[ \mathbf m_i=\frac1{n_i}\sum_{\mathbf x\in D_i}\mathbf x \]

然后，聚类内平方和 (WCSS) 定义为：

\[ \text{WCSS}=\sum_{i=1}^k\sum_{\mathbf x\in D_i}\lVert\mathbf x-\mathbf m_i\rVert^2 \]

该标准函数有一个简单的解释：对于给定的聚类\(D_i\)：均值向量\(\mathbf m_i\)是\(D_i\)中样本的最佳代表，因为它最小化了\(D_i\)中“误差”向量\(\mathbf x-\mathbf m_i\)的平方和。因此，WCSS测量用\(k\)个聚类中心\(\mathbf m_1,\mathbf m_2,\cdots,\mathbf m_k\)表示\(n\)个样本\(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n\)所产生的总平方误差。

WCSS的值取决于样本如何分组到簇中以及簇的数量。最佳分割定义为最小化WCSS的分割。

什么样的聚类问题适合WCSS标准？基本上，当聚类形成紧密的云并且彼此分离得相当好时，这是一个合适的标准，如下所示。

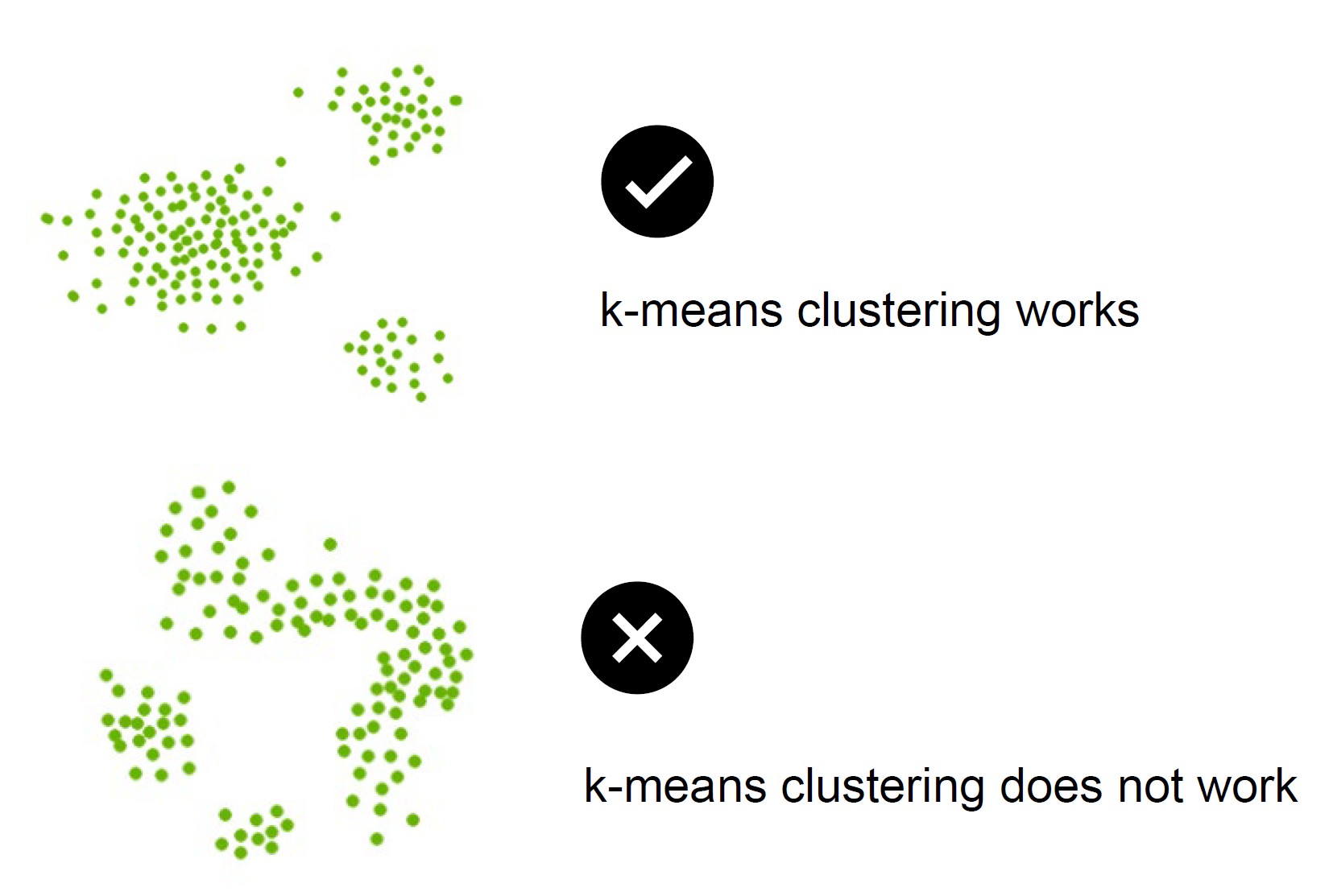
k-Means聚类算法由两个主要操作的迭代组成：

将样本分配到最近的聚类
计算新的聚类中心（质心）

k-Means聚类算法总结如下：

步骤 1：设置数字\(k\)来决定聚类的数量。
步骤 2：随机生成\(k\)个点或质心作为初始聚类中心。它们也可以从数据中随机选择。
步骤 3：将每个数据点分配到它们最近的质心，这将形成预定义的\(k\)聚类。
步骤 4：计算每个聚类的新质心。
步骤 5：重复步骤 3-4，直到质心和样本分配不再发生变化。

如何选择k-Means聚类中的\(k\)值？

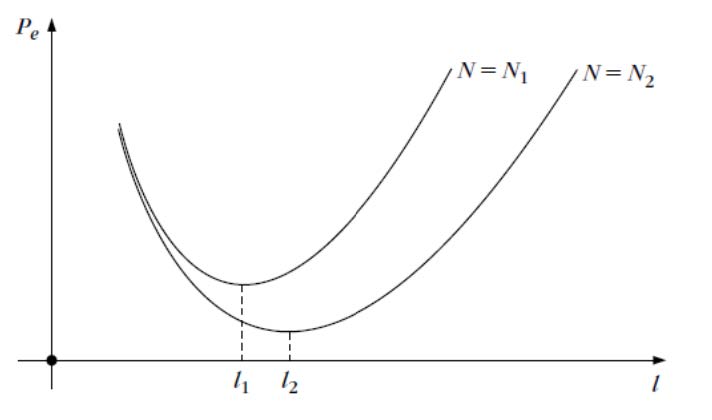
肘部法是查找最佳聚类数的最流行方法之一。此方法使用WCSS，它定义了聚类内总的变化

为了找到聚类的最佳值，肘部法遵循以下步骤：

对给定数据集执行不同k值的k-Means聚类
对于每个k值，计算WCSS值。
绘制WCSS值与k值的曲线
图的弯曲尖点被视为k的最佳值。

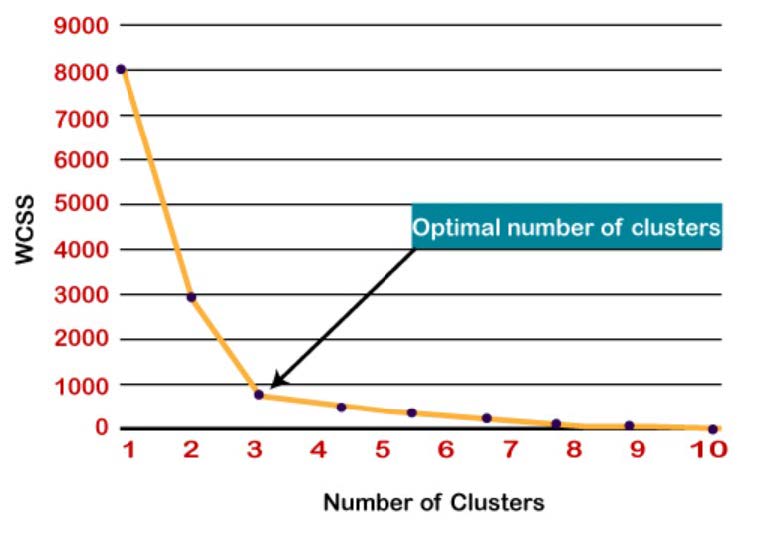
层次聚类

这两个EE6483都讲过了……

层次聚类是概括数据结构属性最常用的方法之一。层次树是样本划分的嵌套集合，用树形图或树状图表示，如下图所示：

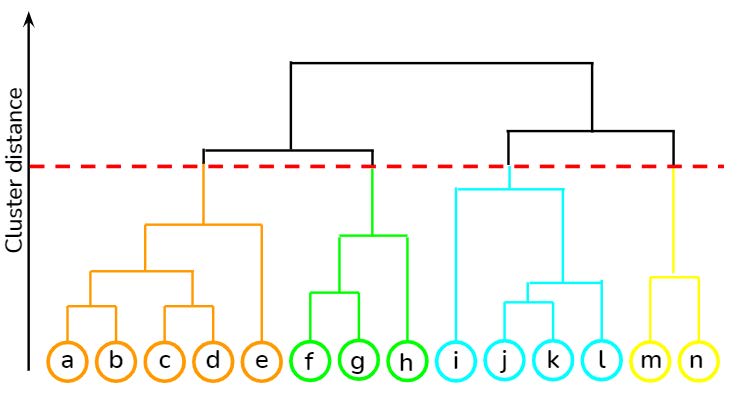
有几种不同的算法可用于查找层次树：

聚合算法，也称为自下而上的方法，从\(N\)个子簇开始，每个子簇只有一个样本，然后依次聚合成对的簇，直到所有簇都合并为一个包含所有样本的簇
分裂算法，也称为自上而下的方法，从包含所有样本的单个簇开始，然后依次拆分簇，直到每个子簇只包含一个样本。

层次聚类的优点是它不需要我们指定簇的数量，这与\(k\)均值聚类算法不同。

基于分布的聚类

在现实生活中，许多数据集可以用高斯分布（单变量或多变量）建模。因此，假设数据来自不同的高斯分布是非常自然和直观的。因此，我们可以尝试将数据集建模为几种高斯分布的混合。这是高斯混合模型（GMM）的核心思想。

在监督学习中，GMM用于对类条件概率密度函数进行建模。在这里，它用于无监督学习中的聚类。

假设数据底层有\(m\)个聚类，每个聚类中的数据服从正态（高斯）分布。那么数据的分布可以建模为：

\[ p(\mathbf x)=\sum_{i=1}^m\alpha_iN(\mathbf x\vert\mu_i,\Sigma_i) \]

其中\(\mu_i\)和\(\Sigma_i\)分别是第\(i\)个高斯分量（即聚类）的均值向量（即聚类中心）和协方差矩阵。\(\alpha_i\)是第\(i\)个高斯分量的权重，

\[ \sum_{i=1}^m\alpha_i=1 \]

GMM模型参数可以使用期望最大化 (EM) 算法进行估计。有关基于EM的GMM模型参数估计的详细信息，请参阅第 3 部分的讲义。

步骤 1：设置数字\(m\)来决定聚类的数量。
步骤 2：用随机值初始化\(\hat\alpha_i(0)\)，\(\hat\mu_i(0)\)，\(\hat\Sigma_i(0)\)
步骤 3：使用期望最大化算法估计高斯混合模型的参数。
步骤 4：高斯分量的均值向量是聚类中心。将每个数据点分配给其最近的聚类中心。

基于密度的聚类

K-Means和层次聚类非常适合寻找球形聚类或凸聚类。换句话说，它们仅适用于紧凑且分离良好的聚类。

但许多真实的数据集可能包含不规则现象，例如：

任意形状的簇
带有噪声的数据。

基于密度的聚类可以解决这些问题。基于密度的噪声空间聚类（DBSCAN）聚类方法是目前最流行的基于密度的聚类方法。

DBSCAN算法基于“聚类”和“噪声”的直观概念。

簇是数据空间中的密集区域，由密度较低的点区域分隔。对于簇中的每个点，给定半径的邻域必须至少包含最小数量的点。

相比之下，密度较低的区域的点则被视为噪声。这与k均值聚类非常不同，在k均值聚类中，每个数据点都被分配到一个聚类中。

DBSCAN 算法使用两个参数：

MinPts：聚集在一起的点的最小数量（阈值），使某个区域被视为密集。例如，MinPts=4 表示至少需要4个点才能形成一个密集的簇
eps (\(\epsilon\))：一种距离测量，用于定位任何点邻域中的点，即，如果两点之间的距离低于或等于“eps”，则它们被视为邻居，即 \(\epsilon\) 邻域。

在这个算法中，我们有3种类型的数据点：

核心点：如果某个点在 \(\epsilon\) 范围内有超过 MinPts 个点，则该点为核心点。
边界点：\(\epsilon\) 范围内的点数少于 MinPts，但位于核心点的邻域内。
噪声或异常值：不是核心点或边界点的点

如果我们探索可达性和连通性两个概念，就能更好地理解这些参数。

可达性表示一个数据点是否可以直接或间接地从另一个数据点访问，而连通性表示两个数据点是否属于同一个簇。就可达性和连通性而言，DBSCAN 中的两个点可能是：

直接密度可达
密度可达
密度连通

如果点（或样本）p 位于核心点 q 的 \(\epsilon\) 邻域内，则 p 可以从点 q 直接密度到达

如果存在一组从 q 到 p 的核心点，则 p 从 q 密度可达。

如果存在一个核心点，且从该核心点出发两个点都是密度可达的，则称这两个点密度连通。

DBSCAN 的参数设置

MinPts

根据经验法则，可以从数据集的维数\(D\)中得出最小值，例如\(\text{MinPts}\geq D+1\)。MinPts的最小值必须至少为3

但是，对于有噪声的数据集，值越大越好，并且会产生更显著的聚类。根据经验，可以使用\(\text{MinPts}=2\cdots D\)，但对于非常大的数据、噪声数据或包含许多重复项的数据，可能需要选择更大的值。

\(\epsilon\)

然后可以通过绘制与\(k=\text{MinPts}−1\)最近邻的距离（从最大值到最小值排序）来选择 \(\epsilon\) 的值。 \(\epsilon\) 的良好值是此图显示“肘部”（最大曲率）的位置。通常，\(\epsilon\) 的值较小是可取的，并且根据经验法则，只有一小部分点应该在此距离内。

DBSCAN 通过检查数据集中每个点的 \(\epsilon\) 邻域来搜索数据集中的聚类。如果数据点的 \(\epsilon\) 邻域包含的邻居数量超过最小值 MinPts，则创建一个以点 p 为核心的新聚类。然后，该算法直接从这些核心点组装密度可达点，以合并所有密度可达聚类。

当没有新点可添加到任何组时，此过程终止。不属于任何聚类的点被视为噪声或异常值。

DBSCAN 算法

步骤 1 设置 MinPts 和 \(\epsilon\) 的值，并从数据集中随机选取一个数据点作为起点。
步骤 2 递归查找其所有密度连通点，并将它们分配到与核心点相同的簇中。
步骤 3 在前面步骤中未访问过的点中随机选择另一个点，然后转到步骤 2
步骤 4 当所有点都被访问后，此过程结束。不属于任何簇的点被视为噪声。

DBSCAN 的优点

DBSCAN 算法对异常值（噪声点）具有很强的鲁棒性。
DBSCAN 非常擅长将高密度簇与低密度簇分离。
与 K-means 不同，DBSCAN 不需要预先指定簇的数量。
DBSCAN 支持具有不规则结构的簇。

DBSCAN 的缺点

DBSCAN 不适用于密度不同的簇。
DBSCAN 算法不是确定性的，因为它会在不同的试验中形成不同的簇。
有时，选择 \(\epsilon\) 的值可能很困难，尤其是当数据处于较高维度时。

降维和分类的特征选择

发表于 2024-11-08

介绍

在前面的部分中，我们在分类器的设计中使用了所有可用的特征。与模式识别相关的一个问题是所谓的维数灾难，它指的是处理高维数据时出现的问题。数据集的维度对应于数据集中存在的特征数量。由于高维数据而导致的与训练机器学习模型相关的困难被称为“维数灾难”。维数灾难的主要方面是数据稀疏性和距离集中。

将特征数量减少到足够小的原因不止一个。计算复杂性是显而易见的。另一个主要原因是分类器的泛化能力。通常，训练样本数量与自由分类器参数数量之比越高，所得分类器的泛化性能就越好。

大量的特征直接转化为大量的分类器参数（例如神经网络中的突触权重，线性分类器中的权重）。因此，对于有限且通常有限数量的训练样本，保持特征数量尽可能少符合我们设计具有良好泛化能力的分类器的愿望。

此部分的主要任务现可概括如下：

给定若干个特征，如何选出最重要的特征，以减少其数量，同时尽可能多地保留其类别区分信息？

这个问题被称为特征选择或特征减少。

这一步非常关键。如果我们选择的特征辨别能力较弱，那么分类器的后续设计将导致性能不佳。另一方面，如果选择信息丰富的特征，分类器的性能将很好。

必须指出的是，文献中关于特征选择和特征提取的术语存在一些混淆。

简单来说，特征选择就是从原始特征中选取一个特征子集，以降低模型复杂度，提高模型的计算效率，提高泛化能力。

特征提取是从原始特征集中提取或导出信息以创建新的特征子空间。特征提取背后的主要思想是压缩数据，以保留大部分相关信息。常用的主成分分析 (PCA) 是一种特征提取方法。

峰值现象

如上所述，为了设计具有良好泛化性能的分类器，训练样本的数量\(N\)必须相对于特征的数量\(l\)（即特征空间的维数）足够大。以设计线性分类器的情况为例：

\[y=\mathbf w^\intercal\mathbf x+w_0\]

未知参数的数量为\(l+1\)。为了对这些参数进行良好的估计，样本数量\(N\)必须大于\(l+1\)。\(N\)越大，估计效果越好，因为我们可以滤除噪声的影响，同时最小化异常值的影响。

实际上，对于有限的\(N\)，通过增加特征数量，可以获得性能的初始改进，但在临界值之后，进一步增加特征数量会导致错误概率增加。这种现象称为峰值现象，如下所示：

上图说明了通过使用特征数量\(l\)和训练数据集的大小\(N\)，人们期望在实践中体验到的总体趋势。

对于\(N_2\gg N_1\)，\(N_2\)对应的误差值低于\(N_1\)产生的误差值，并且当\(l_2\gg l_1\)时会出现峰值现象。
对于\(N\)的每个值，随着\(l\)的增加，误差概率开始减小，直到误差开始增大的临界值。

因此，在实际应用中，如果训练数据较少，则必须使用较少的特征。如果训练数据较多，则可以使用较多的特征以获得更好的性能。

个别特征评估

特征选择的第一步是单独或分开查看每个特征，并测试它们对当前问题的单独判别能力。尽管单独查看特征远非最佳方法，但此过程有助于我们识别和丢弃“坏”特征。这将减轻稍后将介绍的基于集合的特征评估和选择不必要的计算负担。

在这里，我们将介绍两种单独的特征评估方法，基于对良好特征的两种不同解释，包括类可分离性和特征的相关性。

费舍尔比率

如前所述，好的特征应该在不同的类别中采取不同的值。

特征的类可分性可以用Fisher比率来评估。假设两个类中样本的平均值和标准差分别为\(m_1\)、\(\sigma_1\)、\(m_2\)和\(\sigma_1\)，则 Fisher 比率定义为：

\[ R=\frac{(m_1-m_2)^2}{\sigma_1^2+\sigma_2^2} \]

费舍尔比率的分子其实就是类间（或称类间）差异，分母则是类内（或称类内）散度。

从 Fisher 比率可以看出，一个好的特征应该具有：

类间差异大；
类内散度或方差小。

费舍尔比率越大，特征的判别性越强。费舍尔比率通常用于连续变量。

相互信息

一个好的特征应该包含大量信息来决定类标签的值。特征的相关性可以根据特征和类标签之间的互信息来评估。

两个变量的互信息 (MI) 是两个变量之间相互依赖性的度量。更具体地说，它量化了通过观察另一个变量获得的有关一个变量的信息量。

特征\(x\)和类标签\(y\)之间的互信息可以通过以下方式测量：

\[ \text{MI}(x,y)=E(x)+E(y)-E(x,y) \]

其中\(E(x)\)、\(E(y)\)是\(x\)和\(y\)的熵，\(E(x,y)\)是\(x\)和\(y\)的联合熵：

\[ \begin{aligned} E(x)&=-\sum_{u_i\in x}p(x=u_i)\times\log p(x=u_i)\\ E(y)&=-\sum_{c_i\in y}p(y=c_i)\times\log p(y=c_i)\\ E(x,y)&=-\sum_{u_i\in x}\sum_{c_i\in y}p(x=u_i,y=c_i)\times\log p(x=u_i,y=c_i) \end{aligned} \]

其中\(p(x=u_i)\)表示未来\(x\)取\(u_i\)值的概率。互信息通常用于离散特征。

特征子集选择

特征子集选择问题可以定义如下：

给出完整的特征集：

\[ X=\{x_1,x_2,\cdots,x_n\} \]

选择一个子集

\[ Z=\{z_1,z_2,\cdots,z_m\},z_i\in X \]

以产生最佳分类性能。

由于峰值现象，应选择所有可用特征的一个子集并将其用作模式分类模型的输入。上文介绍了对单个特征的评估。是否可以通过简单选择排名靠前的特征来获得特征子集？

答案是否定的。

这是因为排名靠前的特征之间可能存在很强的相关性，这样选择的特征子集可能会表现出严重的冗余。一个好的特征子集应该具有最大的相关性和最小的冗余性。

特征子集选择算法由两个主要部分组成：

搜索算法
评估标准

搜索算法的目标是生成候选特征子集，而评估标准旨在评估搜索算法生成的候选特征子集的优劣，如下所示

搜索算法

穷举搜索法

顾名思义，穷举搜索将穷举所有可能的子集。换句话说，它会生成\(n\)特征的所有可能组合。

穷举搜索当然不会错过最佳特征子集，但如果\(n\)很大，计算复杂度就会过高。实际上，只有当\(n\)很小时才使用穷举搜索。

顺序前向选择

顺序前向搜索是一种自下而上的方法。它从一个空的特征集开始，逐步添加特征以形成特征子集。在每一步中，根据一定的标准在未选定的特征中选择最佳特征。特征子集不断增长，直到满足停止标准。

顺序后向消除

顺序后向消除法是一种自上而下的方法。它从一组完整的特征开始。每次删除一个特征。每次根据某个标准删除最不重要的特征。特征集不断缩小，直到满足停止标准。

评估标准

为了选择一个好的特征子集，我们需要一种测量特征子集准确区分两个或多个类别的能力的方法。这可以通过定义针对可能的特征子集进行优化的类可分离性度量来实现。

我们可以通过两种方式评估特征子集：

分类器的分类性能

在这个方法中，我们在特征子集上训练一个分类器，然后以分类效果作为评价标准。选择特征子集来匹配分类器。不同的分类器可能会选择不同的特征子集。

可分离性度量

这种方法估计了数据来源分布之间的重叠，并倾向于重叠最小的分布，即最大可分离性。这样选择的特征子集与最终使用的分类器无关。此标准不需要训练大量模式分类器，因此在计算上更高效。

缺点是，估计数据分布重叠时所做的假设通常很粗略，可能与真实分布不太吻合。

接下来，介绍一些可分离性度量。

基于Mahalanobis距离的可分离性测量

可分离性可以通过特征子集空间中两个均值向量之间的Mahalanobis距离来衡量。

对于多类问题，我们可以使用成对可分离性度量的总和

\[ J=\sum_i\sum_{j\ne i}J_{i,j} \]

基于散度的可分离性测量

\[ J=\text{Tr}(\mathbf S_W^{-1}\mathbf S_B) \]

或

\[ J=\frac{\text{Tr}(\mathbf S_B)}{\text{Tr}(\mathbf S_W)} \]

其中\(\mathbf S_B\)和\(\mathbf S_W\)分别为类间和类内散度矩阵。\(\text{Tr}(\mathbf A)\)表示矩阵\(\mathbf A\)的迹，定义为\(\mathbf A\)主对角线上元素之和。

特征子集选择算法

特征子集选择算法由搜索算法和特征子集评价标准组成。根据所使用的评价标准，特征选择算法通常分为三类：过滤方法、包装方法和嵌入式方法。

包装方法在循环中包含一个分类器，并使用分类性能（例如准确率或错误率）作为特征子集评价标准。

过滤方法在循环中不包含分类器，而是采用类可分离性度量作为特征子集评价标准。

包装方法

停止标准可以是

已达到要选择的特征数量，或
分类准确率（在验证集上）达到最佳，或
其他

过滤方法

已达到要选择的特征数量，或
可分离性度量不再提高，或
其他

顺序前向特征选择算法

接下来，我们结合顺序前向搜索和评估标准来形成特征选择算法。

将每个特征视为候选特征 \(F^{(i)}=\{x_i\}\) 评估可分离性度量（过滤器） \(J^{F(i)}=\frac{\text{Tr}(\mathbf S_B^{F(i)})}{\text{Tr}(\mathbf S_W^{F(i)})}\) 或者训练分类器并找到分类准确率（包装器） \(C^{F(i)}=\text{Classifier Trained on } F(i)\) \(J^{F(i)}=\text{Accuracy}(C^{F(i)})\) 选择具有最大可分离性（过滤方法）或最佳分类性能（包装器方法）的特征作为第一个特征： \(k=\arg\max J^{F(i)}\) \(z_1=x_k\)
将剩余的\(n-1\)个特征中的每一个视为第二个特征的候选， \(F^{(i)}=\{z_1,x_i\},i\ne k\) 评估可分离性度量（过滤方法）： \(J^{F(i)}=\frac{\text{Tr}(\mathbf S_B^{F(i)})}{\text{Tr}(\mathbf S_W^{F(i)})}\) 或者训练分类器并找到分类准确率（包装方法） \(C^{F(i)}=\text{Classifier Trained on } F(i)\) \(J^{F(i)}=\text{Accuracy}(C^{F(i)})\) 选择达到最大可分离性（过滤方法）或最佳分类性能（包装方法）的特征作为第二个特征。
选择过程持续进行，直到满足停止标准

顺序后向特征消除算法

将每个特征视为要消除的候选特征， \(F^{(i)}=\{x_1,x_2,\cdots,x_n\}-x_i\) 评估相应的可分离性度量（过滤器） \(J^{F(i)}=\frac{\text{Tr}(\mathbf S_B^{F(i)})}{\text{Tr}(\mathbf S_W^{F(i)})}\) 或者训练一个分类器并找到相应的分类准确率（包装器） \(C^{F(i)}=\text{Classifier Trained on } F(i)\) \(J^{F(i)}=\text{Accuracy}(C^{F(i)})\) 找出对可分离性度量（过滤方法）或分类性能（包装方法）影响最小的特征，并将其作为第一个要删除的特征。
消除过程持续进行，直到满足停止标准。

嵌入方法

嵌入式方法结合了过滤器和包装器方法的特性。它由具有内置特征选择方法的算法实现。这种方法最流行的例子是 Lasso（最小绝对收缩和选择运算符,L1正则化），它具有内置机制，通过将与最不重要的特征相关的系数收缩为零来惩罚模型中的特征数量（参见第 8 章）。

\[ \begin{aligned} J_{\text{Lasso}}(\Theta)&=\frac12\left\{\sum_{i=1}^N(\hat y_i-y_i)^2+\lambda\sum_{j=0}^m\lvert\theta_j\rvert\right\}\\ &=\frac12\{(\mathbf y-\Phi\Theta)^\intercal(\mathbf y-\Phi\Theta)+\lambda\lVert\Theta\rVert\} \end{aligned} \]

分类器性能评估

发表于 2024-11-07 更新于 2024-11-08

在监督学习中，分类模型是使用标记数据进行训练的。我们如何了解模型的性能？接下来，我们介绍一些模型评估程序和指标。

评估程序

保留方法

在此方法中，可用数据的一部分/子集被保留下来（这就是“保留”这个名称的由来）用于评估模型。该数据子集用作测试数据，用于评估已训练分类器的性能。

一旦使用训练数据训练了模型，就可以使用训练后的模型预测测试数据的标签。然后将预测值与标签的实际值进行比较。这是可能的，因为测试数据是具有已知标签的可用数据的一部分。模型的性能通过各种指标来衡量，这些指标将在后面介绍。

通常，70%–80%的可用数据（随机抽样）用于分类器训练，剩余的20%–30%用作测试数据。

通常，可用数据分为 3 个部分 - 训练和测试数据以及验证数据。验证数据用于在训练阶段测量模型性能。在通过训练和验证数据确定模型后，测试数据仅使用一次，用于测量和报告模型的最终性能。

该方法的一个明显问题是，不同类别的数据划分为训练数据和测试数据可能不成比例。如果与某些类别相关的数据总体百分比远低于其他类别（即类别不平衡问题），这种情况会更糟。尽管采用随机抽样来选择测试数据，但这种情况仍可能发生。

可以通过应用分层随机抽样代替随机抽样在一定程度上解决此问题。在分层随机抽样中，对每个单独的类别进行随机抽样。例如，每个类别中 70% 和 30% 的样本被随机选择为训练数据和测试数据。这确保生成的随机分区具有相等的每个类别的比例。

重复保留法

保留方法的一种特殊变体称为重复保留，通常用于确保所组成的训练和测试数据集的随机性。

在重复保留中，使用多个随机保留来衡量模型性能。最后，取所有性能的平均值。

由于已抽取多个保留，因此训练和测试数据（以及验证数据，如果已抽取）更有可能包含来自所有类别的代表性数据，并且与原始输入数据非常相似。

K折交叉验证方法

重复保留的过程是k折交叉验证技术的基础。k折交叉验证中，数据集被分成k个完全不同或不重叠的随机分区，称为折叠。

每个\(k\)折叠都有机会用作保留测试集，而所有其他折叠则集体用作训练数据集。在\(k\)保留测试集上共拟合和评估了\(k\)个模型，平均性能报告如下图所示。

留一交叉验证 (LOOCV)

\(k\)折交叉验证的一个极端情况是设置\(k=N\)，即样本总数。在这种极端情况下，在每一折中，只有一个样本用作测试数据，其余\(N-1\)个样本用作训练数据。这种极端情况称为留一交叉验证。

这样做是为了最大化用于训练模型的数据数量。很明显，它必须运行的迭代次数（即倍数）等于数据集中的样本总数。因此，它在计算上非常昂贵，并且仅在样本数量较少时使用。

重复K折交叉验证

通过K折交叉验证估计模型性能可能会很嘈杂。这意味着每次运行该过程时，都会使用不同的数据集拆分为\(k\)折，从而获得不同的模型性能平均估计值。从一次K折交叉验证运行到另一次运行的估计性能差异量取决于训练测试数据划分的差异。

解决该问题的方法之一是多次重复K折交叉验证过程，并报告所有倍数和所有重复的平均性能。这种方法通常称为重复K折交叉验证。

绩效评估指标

对于二分类问题，我们假设一个类是正类，另一个是负类。通常，我们感兴趣的类被命名为正类，例如，“癌症”被命名为正类，而“正常”被命名为负类。样本的分类结果可能有四种情况：

真阳性（TP）：正类样本被正确分类为正类
假阳性（FP）：负类样本被错误分类为正类
真阴性（TN）：负类样本被正确分类为负类
假阴性（FN）：正类样本被错误分类为负类

混淆矩阵

混淆矩阵是分类结果的总结，如下所示：

准确率

准确率是正确分类的样本的比例：

\[ \text{Acc}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}} \]

错误率

错误率是错误分类的样本所占的比例：

\[ \text{Err}=\frac{\text{FP}+\text{FN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}} \]

灵敏度和特异性

分类器的灵敏度衡量被正确分类的正样本的比例。其测量方法如下：

\[ \text{Sensitivity}=\frac{\text{TP}}{\text{TP}+\text{FN}} \]

分类器的特异性衡量被正确分类的负样本的比例。其测量方法如下：

\[ \text{Specificity}=\frac{\text{TN}}{\text{TN}+\text{FP}} \]

精确率和召回率

精确率表示的是真正为正的预测所占的比例：

\[ \text{Precision}=\frac{\text{TP}}{\text{TP}+\text{FP}} \]

召回率衡量的是正确预测的正结果占正结果总数的比例：

\[ \text{Recall}=\frac{\text{TP}}{\text{TP}+\text{FN}} \]

F分数

F分数是分类器性能的衡量标准，它结合了精确度和召回率：

\[ \text F=\frac{2\times\text{Precision}\times\text{Recall}}{\text{Precision}+\text{Recall}} \]

接收者操作特征 (ROC) 曲线

【官方双语】ROC & AUC 详细解释！

在分类问题中，我们使用判别函数来决定样本属于哪个类。在贝叶斯决策规则中，这个判别函数是后验概率。对于二分类问题：

\[ \begin{aligned} \text{Decide }&\omega_1\text{ if }P(\omega_1\vert x)\gt P(\omega_2\vert x)\\ \text{Decide }&\omega_2\text{ if }P(\omega_2\vert x)\gt P(\omega_1\vert x) \end{aligned} \]

在这个决策规则中，我们隐式地假设阈值为0.5。如果属于某个类别的后验概率高于0.5，则样本被分配到该类别。但在某些应用中，例如将患者诊断为“癌症”或“正常”，使用不同的阈值（而不是0.5）可能是更谨慎的选择。

设置不同的阈值来对正类进行分类将不可避免地改变混淆矩阵中的4个指标：TP、FP、TN、FN，从而改变分类模型的其他评估指标。其中一个阈值可能会比其他阈值产生更好的结果，这取决于我们的目标是降低假阴性还是假阳性的数量。

我们可以生成不同的混淆矩阵并比较各种指标。但这样做并不明智。相反，我们可以做的是绘制其中一些指标之间的图，以便我们可以轻松地看到哪个阈值可以给我们带来更好的结果。

ROC曲线正好解决了这个问题。

接收者操作特性 (ROC) 可视化分类模型在检测真阳性同时避免出现假阳性的效率。

我们定义以下措施：

真阳性率（TPR）：\(\text{TPR}=\frac{\text{TP}}{\text{TP}+\text{FN}}=\text{Recall}=\text{Sensitivity}\)
假阳性率（FPR）：\(\text{FPR}=\frac{\text{FP}}{\text{FP}+\text{TN}}=1-\text{Specificity}\)

在 ROC 曲线中，在不同分类阈值下绘制了假阳性率（横轴）与真阳性率（纵轴）。

曲线下面积（AUC），即上图中的阴影部分，是衡量分类器区分类别能力的指标。

当AUC=1时，分类器能够完美地区分所有正类和负类点；
当AUC=0时，分类器会将所有负类预测为正类，将所有正类预测为负类。
当AUC=0.5时，分类器无法区分正类和负类点，这意味着分类器预测的是随机类。
当0.5<AUC<1时，分类器很有可能能够区分正类和负类，这意味着分类器能够检测到的真阳性和真阴性的数量多于假阴性和假阳性的数量。

分类树

发表于 2024-11-06 更新于 2024-11-08

Classification trees

阅读全文 »

视频压缩和标准

发表于 2024-10-24

视频编码和标准

视频压缩基础知识

空间冗余（spatial redundancy）是指图像内（或更具体地说，在小的图像邻域内）像素之间的统计相关性，也被称为帧内冗余（intraframe redundancy）。

时间冗余（temporal redundancy）是指视频序列中连续帧的像素之间的统计相关性，因此，它也被称为帧间冗余（interframe redundancy）。

心理视觉冗余（Psychovisual Redundancy）

频率掩蔽（frequency masking）：人类对高频成分中的噪声或失真不太敏感，反之亦然。
色彩掩蔽（color masking）：人类对亮度成分比色度成分更敏感。

视频压缩的方法：

通过利用视频中的冗余。
- 空间冗余。
- 时间冗余。
- 心理视觉冗余。
通过提高编码效率：
- Huffman编码。
- 预测/差分编码。

视频结构

宏块（Macroblock）

一个宏块包含一个16x16的Y分量以及空间对应的8x8的C_b和C_r分量。

一个宏块有4个亮度块和2个色度块，是进行DCT运算和运动补偿的基本单位。

视频压缩基础知识

视频压缩的主要思想：

运动估计：预测宏块的运动矢量
运动补偿：对预测宏块和实际宏块之间的微小差异进行编码

运动估计与补偿

帧内压缩与帧间压缩

许多视频压缩方法（例如MPEG）都使用帧内压缩和帧间压缩。

帧内压缩

将每个视频帧视为静止图像（例如，MPEG中的I帧）。
减少空间冗余。
采用基于JPEG的压缩。

帧间压缩

利用时间域相关性（例如MPEG中的P帧和B帧）。
减少时间冗余。
采用运动估计和补偿。

色度二次采样（Chroma Subsampling）

二次采样格式：

4:4:4 - 无二次采样
4:2:2、4:1:1 - 水平二次采样
4:2:0 - 水平和垂直二次采样

人类对亮度分量比色度分量更敏感。因此，为了实现压缩，色度分量被进行二次采样。
4:2:2二次采样：对于每两个水平Y样本，采样1个C_b和1个C_r。
4:2:0二次采样：对于每2x2的Y样本，采样1个C_b和1个C_r。

MPEG基础

-目的：对视频信号进行编码/压缩。 - MPEG标准基于DCT编码和运动估计与补偿。 - DCT编码：消除帧内冗余。 - 运动估计与补偿：消除帧间冗余。 - 彩色视频源有三个分量 - 亮度分量（Y） - 两个色度分量（C_b和C_r），通常采用4:2:0二次采样格式。

图片组（GOP）

视频序列被划分为图像组（GOP）。

每个GOP可能包含三种类型的图片：

I帧（帧内编码帧，Intra-coded frames）
P帧（预测编码帧，Predictive-coded frame）
B帧（双向编码帧，Bidirectional-coded frame）

I帧、P帧、B帧

I帧
- 编码时不参考任何其他帧。
- Y、C_b、C_r块使用JPEG算法独立编码。
P帧和B帧
- 称为帧间编码或插值帧。
- P帧使用来自前一个锚I帧或P帧的运动估计和补偿进行编码。
- B帧使用来自过去、未来或两个锚帧的预测进行编码。

运动估计与补偿

时间冗余：视频中连续的帧是相似的。

并非视频的每一帧都需要单独编码。
思路：对当前帧和序列中其他帧之间的差异进行编码。
差异值较小，因此有利于压缩。
视频压缩：
- 运动估计：运动矢量搜索。
- 运动补偿：计算预测误差。

运动估计

MV搜索通常仅限于小范围的邻近区域。水平和垂直位移都在\([−p,p]\)范围内。这使得搜索窗口的大小为\((2p+1)\times(2p+1)\)。

两个宏块之间的差异可以通过平均绝对差异（Mean Absolute Difference，MAD）来测量：

\[\mathrm{MAD}(i,j)=\frac1{N^2}\sum_{k=0}^{N-1}\sum_{l=0}^{N-1}\left\lvert C(x+k,y+l)-R(x+i+k,y+j+l)\right\rvert\]

\(N\)：宏块的大小
\(k\)和\(l\)：宏块中像素的索引
\(i\)和\(j\)：水平和垂直位移
\(C(x+k,y+l)\)：目标帧宏块中的像素
\(R(x+i+k,y+j+l)\)：参考帧宏块中的像素

目标：找到运动矢量\(\mathrm{MV}=(u,v)\)，使得\(\mathrm{MAD}(i,j)\)最小：

\[(u,v)=\arg\min_{(i,j)}\mathrm{MAD}\ ,i\in[-p,p],j\in[-p,p]\]

运动估计方法

全面搜索
三步搜索
2D-Log 搜索
分层搜索
钻石搜索
交叉搜索
等等

全面搜索

搜索搜索窗口内的每个点。
优点：准确、压缩率最高。
缺点：速度慢、计算量大。

三步搜索

仅包含 3 个步骤。

步骤 1：搜索 9 个点以获得最小预测误差。
步骤 2：以步骤 1 中找到的位置为中心，将搜索宽度减半，搜索 9 个点以获得最小误差。
步骤 3：以步骤 2 中找到的位置为中心，将搜索宽度减半，搜索 9 个点以获得最小误差。最终位置是找到的最佳位置。
优点：快速
缺点：准确度较低，压缩率较低。

二维对数搜索

步骤 1：搜索 5 个点以获得最小预测误差。
步骤 2：以前次迭代中找到的位置为中心，
1. 如果找到的位置是中心位置或位于边界，则将搜索宽度减半；否则，保留搜索宽度。
2. 1. 如果搜索窗口尚未达到 3x3，则搜索 5 个点以获得最小误差并重复步骤 2。
  2. 否则，如果搜索窗口为 3x3，则搜索 9 个点以获得最小误差并返回最佳找到位置。
速度：介于完整搜索和 3 步搜索之间。
准确度：介于完整搜索和 3 步搜索之间。

分层搜索

三级分层搜索，原始图像位于第 0 级。
第 1 级和第 2 级的图像是通过从前面的级别按 2 倍的倍数下采样获得的，初始搜索在第 2 级进行。

搜索可从分层/多分辨率方法中受益。
可以从分辨率显著降低的图像中获得运动矢量的初始估计。
宏块的尺寸更小。
搜索范围 p 也可按比例缩小。
因此，所需的操作数量大大减少。

MPEG标准

MPEG-1

由 ISO/IEC 于 1992 年 11 月制定。
有损视频/音频压缩标准。
为数字存储媒体 (VCD) 提供速度为 1.5 Mbps 的视频及其相关音频编码。
JPEG、H.261 的扩展。
仅支持逐行扫描。
支持的图片分辨率：
30 fps 的 NTSC 视频为 352 × 240。
25 fps 的 PAL 视频为 352 × 288。
使用 4:2:0 色度子采样。

MPEG-1 也称为 ISO/IEC 11172。

它有五个部分：

第 1 部分 - MPEG-1 系统
第 2 部分 - MPEG-1 视频
第 3 部分 - MPEG-1 音频
第 4 部分 - 一致性
第 5 部分 - 参考软件

限制：

仅支持逐行扫描。
图像质量低。
压缩率低。

I、P 和 B 帧编码

I帧编码

P帧编码

对目标帧中的每个宏块进行运动估计和补偿。
- 将目标帧中的每个宏块与前一个I或P参考（锚）帧进行比较。
- 对于每个宏块，以参考帧中的搜索窗口为中心进行搜索。
- 如果绝对差和(SAD)小于阈值，则找到匹配项。
- 如果找到匹配项，则确定两个参数：运动矢量和预测误差（矩阵）。
  - 运动矢量测量目标宏块的位置与参考帧中最佳匹配宏块的位置之间的偏移或位移矢量。
  - 预测误差测量目标宏块与参考帧中最佳匹配宏块之间的差异（矩阵）。
  - 运动矢量使用差分编码进行编码，并对得到的符号进行霍夫曼编码。
  - 预测误差（Y、Cr、Cb）的差异矩阵使用与 I 帧相同的步骤进行编码。
- 如果未找到匹配项，则将宏块独立编码为 I 帧中的宏块。

B帧编码

为什么双向搜索：

在前一个和下一个参考帧中找到目标帧的宏块 (MB) 的良好匹配的几率更高。
例如，目标帧中包含球的一部分的 MB 无法在前一帧中找到良好的匹配 MB。
但是，可以从下一帧轻松获得匹配。

对于目标帧中的每个宏块，针对前一个（前一个）和后一个（后一个）参考（锚点）I 帧或 P 帧执行运动估计和补偿。
这会产生 2 组（运动矢量、差异矩阵）对，一组基于前一个锚点帧，另一组基于后一个锚点帧。
使用目标宏块以及前一个和后一个最佳匹配宏块的平均值计算第三个差异矩阵。
选择具有最小预测误差的集合，并以与 P 帧相同的方式对其进行编码。

帧大小

P帧明显小于I帧，因为利用了时间冗余。
B帧甚至比P帧还要小，因为具有双向预测的优势。

MPEG-2

旨在解决 MPEG-1 的局限性：例如，低比特率（1.5 Mbps）、仅逐行扫描。
1995 年标准化。
为高比特率（4 Mbps）的数字广播电视（隔行扫描）开发。
为不同的应用定义不同的配置文件。
支持可扩展编码。

可扩展性

可扩展编码对于通过具有以下特征的网络传输的MPEG-2视频非常有用：

比特率差异很大的网络。
具有可变比特率 (VBR) 通道的网络。
具有噪声连接的网络。

可扩展编码

分层编码：一个基础层和一个或多个增强层。
基础层可以独立编码、传输和解码以获得基本视频质量。
首先发送基础层的比特流，以便为用户提供快速和基本的视频视图，然后发送增强层以提高质量。
但是，增强层的编码和解码依赖于基础层或先前的增强层。

可扩展性种类

SNR可扩展性：增强层提供更高的SNR。
空间可扩展性：增强层提供更高的空间分辨率。
时间可扩展性：增强层有助于提高帧速率。
混合可扩展性：这结合了上述三种可扩展性中的任意两种。
数据分区：量化DCT系数被分成多个分区。

SNR可扩展性

对基础层进行增强以提高信噪比(SNR)。
在两层生成输出比特流Bits_base和Bits_enhance：
- 基础层对DCT系数进行粗量化，导致位数较少且视频质量相对较低。
- 粗量化的DCT系数随后进行逆量化(Q^-1)并馈送到增强层以与原始DCT系数进行比较。
- 它们的差异被精细量化以生成DCT系数细化，经过VLC后，变为称为Bits_enhance的比特流。

空间可扩展性

基础层用于生成降低分辨率图片的比特流。
与增强层结合时，生成原始分辨率的图片。

时间可扩展性

输入视频在时间上被解复用为两部分，每部分承载原始帧速率的一半。
基础层编码器对其自己的输入视频执行正常的单层编码程序，并产生输出比特流 Bits_base。

混合可扩展性

以上三种可伸缩性中的任意两种可以组合形成混合可伸缩性：
- 空间和时间混合可伸缩性。
- SNR和空间混合可伸缩性。
- SNR和时间混合可伸缩性。
通常采用由基础层、增强层1和增强层2组成的三层混合编码器。

数据分区

基础分区包含低频DCT系数。
增强分区包含高频DCT系数。
严格来说，数据分区不是分层编码：
- 因为单个视频数据流被简单地分割。
- 在生成增强分区时不再依赖基础分区。
适用于通过嘈杂的信道进行传输和渐进式传输。

相对于MPEG-1的优势

在同等比特率下，图像质量比MPEG-1更好。
支持逐行和隔行扫描，而MPEG-1仅支持逐行扫描。
支持可扩展性，而MPEG-1不支持。
更好地抵御比特错误。MPEG-2可以在嘈杂且不可靠的网络上传输带有比特错误的视频。
支持 4:2:2 和 4:4:4 色度子采样以提高色彩质量。
更灵活的视频格式，支持DVD和HDTV定义的各种图像分辨率。

H.26x标准

H.264

2003年由ITU-T VCEG和ISO/IEC MPEG标准化。
也称为高级视频编码(AVC)或MPEG-4第10部分。
压缩效率比H.262高50%，比H.263高30%。
应用：互联网视频、计算机、高清电视广播、蓝光盘、移动和便携式设备。
通过可变块大小、多参考帧改进运动补偿。

主要特点

4×4块中的整数变换。低复杂度，无漂移。
可变块大小运动补偿，亮度图像中从16×16到4×4。
通过插值实现运动矢量的四分之一像素精度。
多参考图像运动补偿。
帧内方向空间预测。
循环内去块滤波。
上下文自适应可变长度编码 (CAVLC) 和上下文自适应二进制算术编码 (CABAC)
对数据错误和数据丢失更具鲁棒性。
采用混合编码
- 帧内空间预测。
- 帧间运动预测。
- 对残差进行变换编码。

运动补偿

可变块大小运动补偿。
两种类型：16×16宏块（M类型）和8×8分区（8×8类型）。
默认情况下，宏块的大小为 16×16。
可以进一步划分为更小的分区。

在亮度图像中，运动补偿的精度为四分之一像素精度。
半像素和四分之一像素位置的像素值可以通过插值得出。
使用6抽头滤波器估算半像素位置的像素值（b和h）：

\[ \begin{aligned} b_1&=E-5F+20G+20H-5I+J\\ h_1&=A-5C+20G+20M-5R+T\\ \end{aligned} \]

\[ \begin{aligned} b&=(b_1+16)\gg5\\ h&=(h_1+16)\gg5\\ \end{aligned} \]

请注意，>>为按位右移。
b 和 h 被剪裁到图像范围，例如 0-255。

GOP中的附加选项

无 B 帧
- B 帧中的宏块预测会导致更多延迟和存储。
- 在此选项中，仅允许 I 帧和 P 帧。
- 压缩效率相对较低。
- 更适合某些应用，例如视频会议。
- 与 H.264 的 Baseline Profile 或 Constrained Baseline Profile 兼容。
多个参考帧
- 为了在 P 帧中找到每个宏块的最佳匹配，H.264 最多允许 N 个参考帧。
- 提高压缩效率。
- 需要更多计算。

整数变换

DCT会因为浮点计算和变换与逆变换中的舍入误差而导致预测偏移。
它可能累积起来，导致较大的误差。
在H.264中，整数变换用于解决该问题。
H.264提供具有非线性步长的量化方案，以获得准确的速率控制。
2D DCT 可以通过两个连续的1D变换实现。
令\(\mathbf f\)为4×4输入矩阵，\(\mathbf F\)为DCT变换数据，\(\mathbf T\)为DCT矩阵：

\[ \mathbf F=\mathbf T\times\mathbf f\times\mathbf T^\intercal \]

4x4 DCT 矩阵由以下公式给出：

\[ \mathbf T_4= \begin{bmatrix} a&a&a&a\\ b&c&-c&-b\\ a&-a&-a&a\\ c&-b&b&-c \end{bmatrix}\\ \begin{cases} a=\frac12\\ b=\frac1{\sqrt2}\cos\frac\pi8\\ c=\frac1{\sqrt2}\cos\frac{3\pi}8 \end{cases} \]

为了导出缩放的4×4整数变换，我们可以简单地将\(\mathbf T_4\)的条目向上缩放并将它们四舍五入为最接近的整数

\[ \mathbf H=\mathrm{round}(\alpha\cdot\mathbf T_4) \]

设\(\alpha=2.5\)，得到4x4整数DCT矩阵

\[ \mathbf H= \begin{bmatrix} 1&1&1&1\\ 2&1&-1&-2\\ 1&-1&-1&1\\ 1&-2&2&-1 \end{bmatrix} \]

\(\mathbf H\)是正交的。但是，它的行不再具有相同的范数。
归一化步骤推迟到量化步骤。
逆变换：

\[ \mathbf H_{\mathrm{inv}}= \begin{bmatrix} 1&1&1&\frac12\\ 1&\frac12&-1&-1\\ 1&-\frac12&-1&1\\ 1&-1&1&-\frac12 \end{bmatrix} \]

令\(\mathbf f\)为4×4输入矩阵，\(\hat{\mathbf F}\)为量化变换输出。
正向整数变换，缩放和量化：

\[ \hat{\mathbf F}=\mathrm{round}\left[\left(\mathbf H\times\mathbf f\times\mathbf H^\intercal\right)\cdot\frac{\mathbf M_{\mathbf f}}{2^{15}}\right] \]

其中，“×”表示矩阵乘法，“·”表示元素乘法，\(\mathbf M_{\mathbf f}\)是由矩阵\(\mathbf m\)和量化参数QP得到的4×4量化矩阵。

令\(\hat{\mathbf f}\)为去量化然后逆变换的结果。缩放、去量化和逆整数变换为：

\[ \hat{\mathbf f}=\mathrm{round}\left[\frac{\mathbf H_{\mathrm{inv}}\times\left(\hat{\mathbf F}\cdot\mathbf V_i\right)\times\mathbf H_{\mathrm{inv}}^\intercal}{2^6}\right] \]

其中\(\mathbf V_i\)是由矩阵\(\mathbf v\)和量化参数QP得到的4×4反量化矩阵。

帧内编码

使用一些相邻的重建像素来预测帧内编码宏块。
可以选择不同的帧内预测块大小（4×4或16×16）。
4×4 块有九种预测模式。
16×16 块有四种预测模式。
对于每种预测模式，将比较预测值和实际值以产生预测误差/残差。
产生最小残差的模式将被选为该块的预测模式。
然后将残差发送到变换编码，其中采用 4×4 整数变换。

H.264比特流结构

新兴的编码和标准

人工智能模型与架构

发表于 2024-10-24

卷积神经网络 (CNN)

简介

由深层组成，以逐步提取更高级别的抽象特征。
常用于分类和回归应用。

线性分类器

大脑视觉皮层：大脑皮层的主要区域，接收、整合和处理从视网膜传递的视觉信息。

损失函数

我们如何确定W和b？
我们需要一个损失函数（误差测量），它是训练期间预测值和输出目标值（教师）之间的度量/距离。
损失函数取决于我们要解决的问题类型。
两个常见问题：
- 回归
  - 目标输出是连续值。
  - 例如，股价预测、降雨量估计等。
- 分类
  - 预测输入的标签/类别。
  - 目标输出是离散的（来自一组可能的标签）。
  - 例如，癌症分类（二进制）、人脸识别（多类）。

常用回归损失函数

平方损失：

\[ L(x,y)=\sum_i(y_i-f(x_i))^2 \]

均方误差 (MSE)：

\[ \mathrm{MSE}=\frac1N\sum_i(y_i-f(x_i))^2 \]

平均绝对误差 (MAE)：

\[ \mathrm{MAE}=\frac1N\sum_i\lvert y_i-f(x_i)\rvert \]

\(x\)和\(y\)是输入数据和目标输出值，\(f(x)\)是网络预测输出。

常用分类损失函数

Softmax损失：具有softmax正则化的交叉熵损失。

\[ p_j=\frac{\mathrm e^{z_j}}{\sum_k\mathrm e^{z_k}},\ \text{where}\ z_j=f(x_j)\\ L=-\sum_jy_j\ln p_j \]

卷积神经网络 (CNN)

CNN架构

卷积层
激活函数层
池化层
全连接 (FC) 层 / 线性层
Softmax层

卷积层

以分层方式提取特征。
前几层提取低级特征，而后几层提取高级特征。
通过卷积核共享权重来减少要训练的参数。

激活函数层

池化层

降低激活图维度，从而减少计算和存储需求。
常见池化操作：最大池化、平均池化。
激活图/特征图的每个通道独立运行。

Softmax层

将最后一层 FC 层的输出分数 (logits) 映射到分类问题的概率中。
根据概率计算 Softmax 损失。

CNN 训练与优化

目标是最小化/优化损失函数。
常见策略以随机梯度下降 (SGD) 及其变体为中心。
使用计算图计算梯度下降和参数更新

知名 CNN 架构

应用

循环神经网络 (RNN)和长短期记忆 (LSTM)

一种专门处理序列的神经网络。
常用于涉及时间序列和状态序列预测和建模的应用。
示例应用：股票价格预测、语言翻译。

循环神经网络 (RNN)

RNN 是一类神经网络，其输入形式为序列数据，例如时间序列数据。
常用于时间/序列数据的分析。
广泛应用于自然语言处理 (NLP)、机器翻译、图像字幕等应用。

RNN 训练与优化

长短期记忆 (LSTM)

• 一个可以随时间维持其状态的记忆单元。 • 由单元状态 (\(c_t\))、隐藏状态 (\(h_t\)) 和 4 个门 (\(i\)、\(f\)、\(o\)、\(g\)) 组成。 • \(c_t\)：长期记忆，\(h_t\)：短期记忆。 • 单元状态 (\(c_t\)) 通过忘记旧记忆（通过忘记 (\(f\)) 门）和添加新记忆（通过输入 (\(i\)) 门和门 (\(g\)) 门）发生变化。 • 通过将单元状态 (\(c_t\)) 传递到输出门来更新隐藏状态 (\(h_t\))。 • 门控制信息流向记忆。 • 门通过 sigmoid/tanh 层获得，它们使用逐点乘法运算符更新 \(c_t\) 和 \(h_t\) 单元状态。

应用

Transformer

一种使用注意力机制并行处理输入序列的网络。
擅长对长程依赖性进行建模。
在许多视觉和NLP应用中实现最先进的性能。

注意力机制用于确定哪些输入标记（例如，NLP 中的单词、CV 中的图像块）与当前输入/标记相关。
注意力机制通过两个向量之间的相关性（点积）计算得出。
相关性 -> 相似性/相关性/重要性 -> 注意力
每个输入标记生成 3 个向量：查询 (q)、键 (k) 和值 (v)。这些向量通过线性映射 (WQ、WK、Wv) 提供更灵活的表示，以学习输入标记之间的潜在关系/注意力。
注意力使用以下方法计算：
- 步骤 1：计算查询 (q) 和键 (k) 向量之间的相关性 (点积)。
- 步骤 2：使用 Softmax 函数对步骤 1 中的相关值进行缩放和规范化。
- 步骤 3：将步骤 2 中的输出乘以相应的值 (v) 向量并将它们相加。

Transformer 使用注意力机制并行处理输入序列。
使用注意力机制和密集/前馈/MLP 层。
高度可并行化。
可以提供全局注意力。
擅长建模长程依赖关系。
在许多视觉和 NLP 应用中实现最先进的性能。
引领其他 SOTA 方法，如 BERT：用于语言的深度双向 Transformer 的预训练。

最初设计用于神经机器翻译。
后来扩展到视觉任务，如识别、检测等，并取得了巨大成功。
利用注意力机制来分析一个 token（单词/图像块）相对于其他 token/图像块的重要性。
由 transformer 编码器和 transformer 解码器组成。

Transformer编码器

输入预处理：
- 将输入单词/标记（例如法语单词）映射到文本嵌入/向量中。
- 添加输入单词的位置编码信息。
编码器：
- 使用注意机制将预处理中的输入向量映射到上下文向量中。
- 上下文向量通过前馈层生成编码器输出。
- 由于注意机制，编码器输出比输入向量具有更好的表示，因为它们利用了其他输入标记的上下文信息。

Transformer解码器

输出预处理：
- 将输出单词/标记（例如英文单词）映射到文本嵌入中。
- 添加输出单词的位置编码信息。
解码器：
- 输出掩蔽自注意力：将输出向量映射到输出单词（例如英文单词）的上下文向量中。掩蔽用于在训练期间隐藏看不见的单词。
- 编码器解码器自注意力（或交叉注意力）：在自注意力阶段的上下文向量（例如英文单词）和编码器输出（例如法语单词）之间执行交叉注意力。
- 结果向量通过前馈层生成解码器输出。
- 解码器输出利用（1）英文单词的自注意力和（2）法语-英文单词交叉注意力来获得更好的表示。
输出后处理：
- 使用 Softmax 函数将解码器输出映射到概率中以生成下一个输出单词（即英文单词）。