遗传算法1

发表于 2024-08-24 更新于 2024-09-11

问题分类、自然选择、遗传算法基础

前言

由于学业等问题，为了能够自我约束，现在暂时重启此博客。

由于Hexo搭建的博客存在各种问题，此次重启预计使用到毕业或者正式工作，届时将尝试转向Wordpress，以进行长久运行。

问题的分类

问题可以用不同的方式分类：

黑盒模型
搜索问题
优化 vs. 条件满足
P/NP问题

黑盒模型

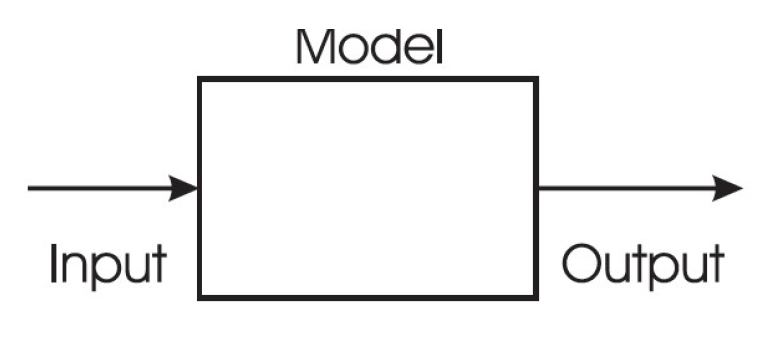
黑盒模型包含3个部分：输入、模型、输出。当其中任何一个部分未知时，就是一种新的问题类型。

优化

当模型和输出已知时，需要寻找满足条件的输入。

例如：

旅行推销员问题（TSP）：输入：一条合适的路径；模型：模拟路径行进；输出：该路径距离
8皇后问题：输入：一个合适的摆放方案；模型：检测是否冲突；输出：是否是合适的方案

建模

当输入和输出已知时，需要构建满足条件的模型（解决方案）。也可以转换为优化问题。

例如：

机器学习构建预测模型

模拟

当输入和模型已知时，需要计算它们的输出。

例如：

天气预报
生物繁殖进化：输入：现存基因库；模型：染色体自由组合和基因变异

搜索问题

建模问题和优化问题比模拟问题的搜索空间大得多。

优化 vs. 条件满足

目标函数（Objective function）：一种为可能的解决方案赋值的方式，该值反映了解决方案的质量

TSP问题：最小化路径长度
八皇后：最大化不冲突的皇后数量

约束条件（Constraint）：二元评估，判断给定要求是否成立（True/False）

约束优化问题（Constrained optimisation problem，COPs）：寻找在满足所有约束条件的情况下，最大/小化目标函数的情况。
约束满足问题（Constraint satisfaction problem，CSPs）：寻找所有满足约束条件的情况。
Free optimisation problem：寻找最大/小化目标函数的情况。
No Problem：没有要解决的问题

P/NP问题

定义问题复杂度的问题。

P类问题：能够在多项式复杂度时间以内解决的问题。
NP类问题：能够在多项式复杂度时间以内验证一个解的问题（例如TSP）。
NP-完全问题（NPC问题）：是NP问题，其他NP问题都可在多项式复杂度时间内规约为该问题。
NP-困难问题：其他NP问题都可在多项式复杂度时间内规约为该问题。

NPC和NPHard非常困难，了解即可。

进化计算

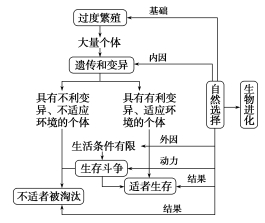
简化版达尔文进化论 - 自然选择学说

自然选择的基础：生物的过度繁殖
进化的动力和自然选择的手段：由于资源有限，需要进行生存斗争
- 种内斗争
- 种外斗争
- 生物与无机环境间的斗争
生物进化的内因：遗传变异
- 变异是不定向/随机的
- 遗传的作用：有利于微小有利变异的积累
自然选择的结果：适者生存（Survival of the fittest）
- 生物产生的不定向变异，由自然选择决定其保存或淘汰
- 自然选择只选择与环境相适应的变异类型，通过多次选择，生物微小的变异得到积累

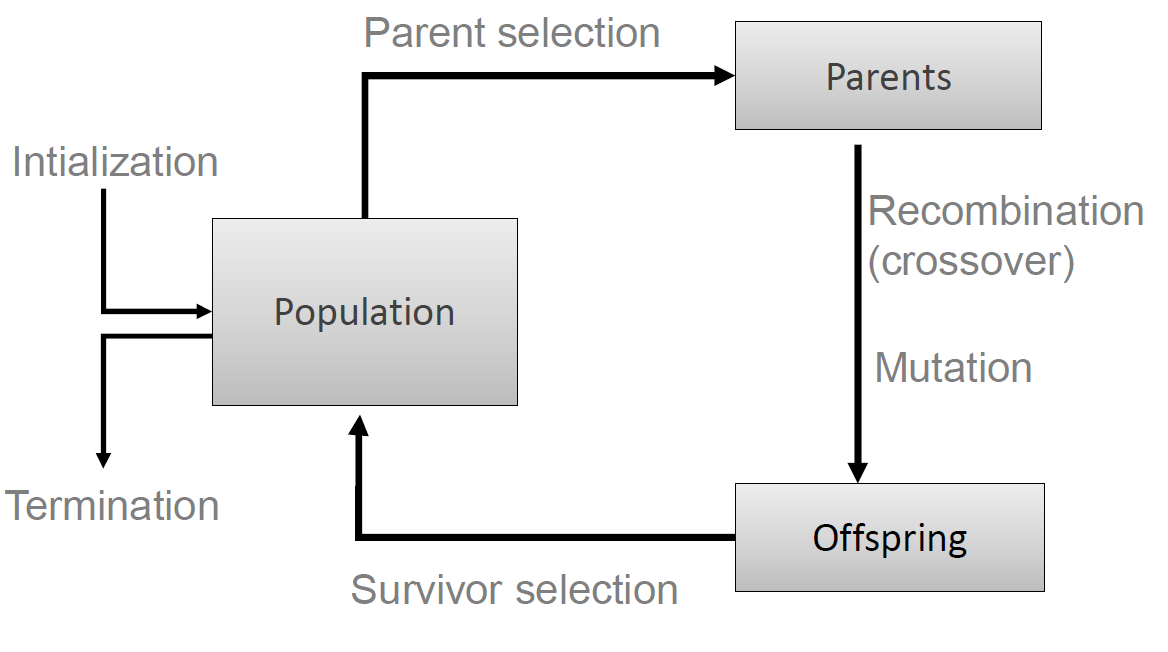
进化计算的内涵

种群生活在资源有限的环境中
对资源的竞争导致更适应环境的个体被筛选出来
这些个体作为种子，通过基因重组和基因突变产生新的个体
对新个体的适应性进行评估，并进行生存斗争（也可能与父母竞争）。
随着时间的推移，自然选择将导致种群适应能力的提高

进化算法属于“生成并测试”算法类别，是基于种群的随机算法。

变异算子（重组和突变）创造了必要的多样性，从而促进了新颖性；自然选择减少了多样性，并起到了推动质量的作用。

begin
    INITIALIZE population(random);
    EVALUATE each candidate;
    REPEAT UNTIL (TERMINATION CONDITION satisfied) DO
        SELECT parents;
        RECOMBINE pairs of parents;
        MUTATE the resulting offspring;
        EVALUATE new candidates;
        SELECT individuals for the next generation;
    OD
end

表示

提供可通过变异运算符操作的候选解决方案的代码。

表现型（phenotype）：原始问题情境中的对象，外在
基因型（genotype）：表示该物体的代码，内在（染色体，DNA）

映射关系，函数f(基因型)=表现型

例如：表现型：十进制整数\(\leftrightarrow\)基因型：二进制

进化函数

表示要解决的任务、要适应的要求（环境）
允许提供比较依据进行自然选择

为每个表现型分配一个实值适应度，作为选择的基础，因此，种类越多（不同的值）越好。

种群

一些复杂的进化算法还会使种群具有空间结构，例如网格。

选择算子通常考虑整个种群，即繁殖概率与当前一代有关。

种群的多样性是指存在的不同适应度/表型/基因型的数量（注意：不是一回事）。

选择机制

通常是概率性的：

高质量的解决方案比低质量的解决方案更有可能被选中
但不能保证
当前种群中最差的通常也有不为零的概率被选中

这种随机性可以帮助摆脱局部最优的问题。

生存者选择：大多数进化算法使用固定的种群规模，因此需要一种从(父母+后代)到下一代的方式。通常是确定性的（而父母选择通常是随机的）

基于适应度：例如，对(父母+后代)进行排序，并取最佳
基于年龄：生成与父母一样多的后代并删除所有父母
有时是随机性和确定性（精英主义）的结合

变异运算符

作用：产生新的候选解决方案。

通常根据其参数数量分为这几种类型

参数 =1：变异运算符
参数 >1：重组运算符
参数 =2：通常称为杂交
参数 >2：理论可能，但在进化计算中很少使用

变异

作用：产生小的随机差别

随机性元素至关重要，并将其与其他一元启发式运算符区分开来

重要性取决于类型：

二元遗传算法：负责保持和引入多样性的后台操作符
FSM/连续变量的EP：仅作为搜索运算符
GP：几乎不用

例如：11111111\(\rightarrow\)11110111

重组

作用：将父母的信息合并传递到后代中

选择合并哪些信息是随机的，大多数后代可能比父母更糟糕，或者和父母一样。希望有些个体能通过结合基因型的元素而变得更好，从而产生良好的特性。

例如：1111/111+0000/000\(\rightarrow\)1111/000+0000/111

初始化/终止

初始化通常随机进行，但需要确保可能的等位基因值的均匀分布和混合，可以采用现有的解决方案，或使用针对具体问题的启发式方法，进行基因的分配。

每代都会检查终止条件：

达到（已知/希望）的适应水平
达到允许的最大代数
达到最低限度的多样性
达到特定代数，但适应度没有改善

没想到周六图书馆提前关门，失策了。明天去Gaia继续。