遗传算法2

八皇后问题

回溯

P1219 [USACO1.5] 八皇后 Checker Challenge

由于很久没有写过代码了，决定先复习一下。

最简单毫无优化DFS法

#include <cstdio>

int n, table[20], flag;

int sol_cnt;

inline int abs(const int &n) { return n < 0 ? -n : n; }

void dfs(const int &cur) {
  if (cur > n) {
    if (++sol_cnt <= 3) {
      for (int i = 1; i <= n; ++i) {
        printf("%d ", table[i]);
      }
      putchar('\n');
    }
  } else {
    for (int i = 1; i <= n; ++i) {
      flag = 1;
      if (cur > 1) {
        for (int j = 1; j < cur; ++j) {
          if (table[j] == i || abs(table[j] - i) == abs(j - cur)) {
            flag = 0;
            break;
          }
        }
      }
      if (flag) {
        table[cur] = i;
        dfs(cur + 1);
      }
    }
  }
}

int main(int argc, char **argv) {
  scanf("%d", &n);
  dfs(1);
  printf("%d\n", sol_cnt);
  return 0;
}

可以标记行列对角线，判断更容易，但是既然能AC就懒得改了。

遗传算法

肯定是不能上洛谷做了，总之先尝试按课件上面的写写吧，网上写的大部分都看不懂（悲）。

个体的定义

gene[i]表示第i列的皇后在第i行。

由于皇后不能在同一列同一行，那么合适的个体的gene[i]必定各不相等，按照0-7初始化。

penalty为处罚机制，每有一对冲突的皇后，该值就上升1。penalty越小越好，若为0则找到了一种解法。

struct Individual {
  int penalty;
  int gene[table_size];
  Individual() {
    this->penalty = 0;
    for (int i = 0; i < table_size; ++i) this->gene[i] = i;
  }
  void update() {
    this->penalty = 0;
    for (int i = 0; i < table_size; ++i) {
      for (int j = i + 1; j < table_size; ++j) {
        this->penalty += Abs(i - j) == Abs(this->gene[i] - this->gene[j]);
      }
    }
  }
  bool operator<(const Individual &x) const {
    return this->penalty < x.penalty;
  }
  bool operator>(const Individual &x) const {
    return this->penalty > x.penalty;
  }
  int &operator[](const int &idx) { return this->gene[idx]; }
  const int &operator[](const int &idx) const { return this->gene[idx]; }
  friend std::ostream &operator<<(std::ostream &os, const Individual &x) {
    for (int i = 0; i < table_size - 1; ++i) os << x[i] << ' ';
    os << x[table_size - 1];
    return os;
  }
} population[quantity];

初始化

将初始个体的基因序列打乱。

void Initialize() {
  std::srand(unsigned(std::time(nullptr)));

  for (int i = 0; i < quantity; ++i)
    std::random_shuffle(population[i].gene, population[i].gene + table_size);

  best.penalty = 0x7fffffff;
}

变异

根据课件上写的，方法为随机交换两个皇后的行。

void Mutation(Individual &x) {
  int tmp[] = {0, 1, 2, 3, 4, 5, 6, 7};
  std::random_shuffle(tmp, tmp + 8);

  std::swap(x[tmp[0]], x[tmp[1]]);
}

重组

首先随机选择基因断开的位置，然后按照如下方法：

1. 保留a1段
2. b2段从头到尾，若有a1段没有的值，则加到a1段后面
3. b1段从头到尾，若有a1段没有的值，则加到a1段后面

两个反过来再来一遍即可。

Individual OneSide(const Individual &a, const Individual &b, const int &pos) {
  Individual ret = a;
  std::set<int> vis(ret.gene, ret.gene + pos);

  for (int i = pos, cur = pos; cur < table_size; ++i) {
    if (!vis.count(b[i % table_size])) {
      ret[cur++] = b[i % table_size];
      vis.insert(b[i % table_size]);
    }
  }

  return ret;
}

std::pair<Individual, Individual> Recombine(const Individual &a,
                                            const Individual &b) {
  int pos = std::rand() % 7 + 1;
  std::pair<Individual, Individual> ret;

  ret.first = OneSide(a, b, pos);
  ret.second = OneSide(b, a, pos);

  return ret;
}

选择

每次尝试插入一个新的后代，将种群从优到劣排序，找到第一个比该后代劣质的个体并替换。

void Insert(Individual &x) {
  x.update();
  for (int i = 0; i < quantity; ++i) population[i].update();
  std::sort(population, population + quantity);

  for (int i = 0; i < quantity; ++i) {
    if (population[i] > x) {
      population[i] = x;
      return;
    }
  }
}

世代更替

1. 计算上一代适应度并记录
2. 选择最好的2个个体杂交
3. 为了插入新个体进行选择
4. 对每个个体进行变异（10%概率，感觉课件上的80%有点大）

void Generate() {
  for (int i = 0; i < quantity; ++i) population[i].update();
  std::sort(population, population + quantity);

  if (population[0] < best) best = population[0];

  std::pair<Individual, Individual> offspring =
      Recombine(population[0], population[1]);

  Insert(offspring.first);
  Insert(offspring.second);

  for (int i = 0; i < quantity; ++i)
    if (rand() % 100 < 10) Mutation(population[i]);
}

测试结果

每次都不一样，毕竟是随机的（）

进行100代的更替，有时候能找到解法，有时候不能。进行10000代的更替，则几乎每次都能找到解法。

---

典型的进化算法行为：

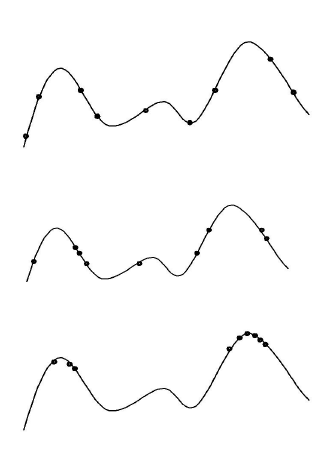一维适应度优化阶段的情景

• 初期阶段：拟随机种群分布
• 中期阶段：种群分布在山丘周围
• 末期阶段：种群集中在山上

长时间运行有益吗？

• 这取决于你有多想取得最后的进展
• 多进行短时间运行可能会更好

是否值得花费精力进行智能初始化？

• 如果存在好的解决方案/方法，那可能很好
• 需要小心，请参阅有关杂交的章节/讲座（讲了吗？？？）

进化算法的背景

对于大多数问题，针对特定问题的工具可以：

• 在大多数情况下比通用搜索算法表现更好
• 效用有限
• 并非在所有情况下都表现良好

目标是提供强大的工具能够提供：

• 表现均匀良好
• 解决一系列问题和情况

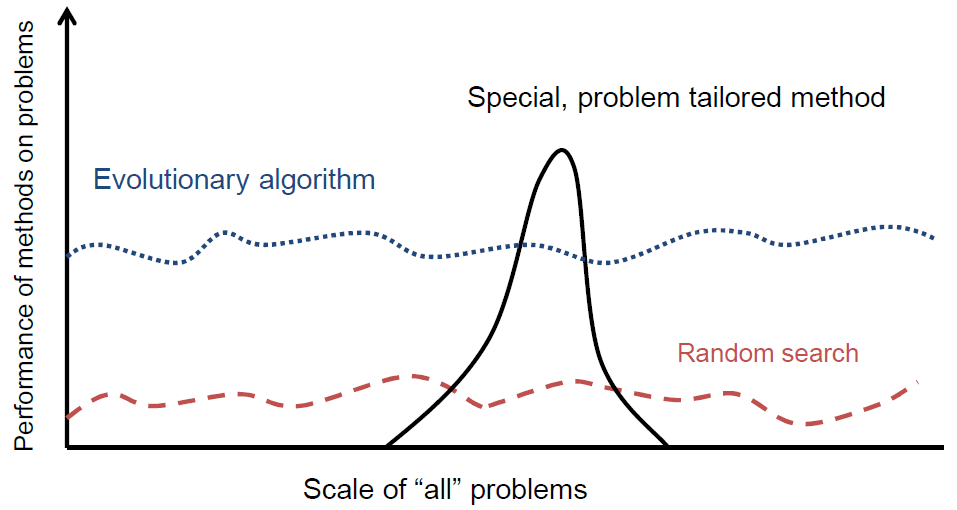
90年代的趋势：向进化算法添加问题特定知识（特殊变异运算符、修复等）

结果：EA表现曲线“变形”：

• 更好地解决给定类型的问题
• 与给定类型不同的问题更糟糕
• 增加的知识量是可变的

最近的理论表明，寻找“万能”算法可能是徒劳的（怎么可能有…）

---

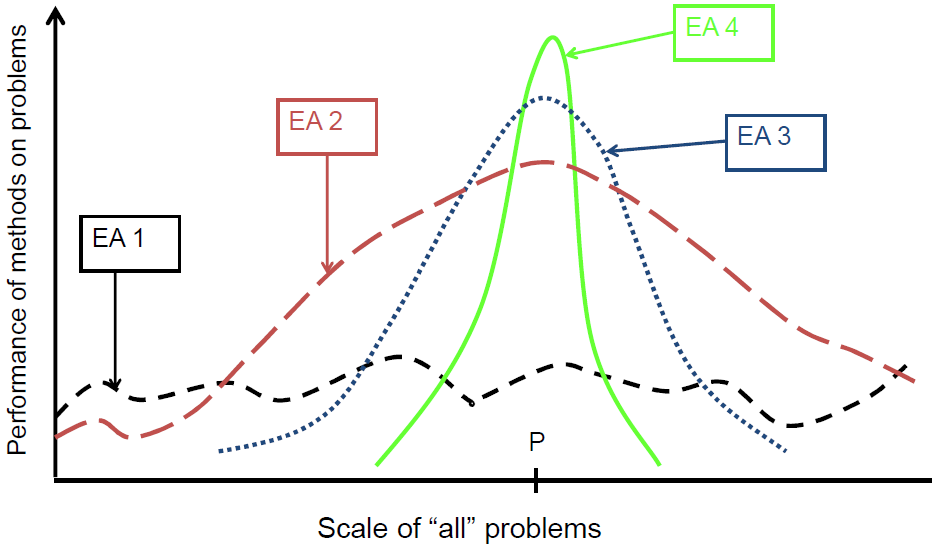
好像上堂课就讲到这，那这篇就到这里为止吧。

---

原来后面还讲了一点，添上添上

进化计算和全局优化

全局优化：从某个固定集合S中寻找最佳解决方案x*

确定性方法

我不在乎它是否有效，只要它能收敛就行

• 例如盒子分解（分支定界等）
• 保证找到x*，
• 可能对运行时间有限制，通常是超多项式

启发式方法（生成和测试）

我不在乎它是否收敛，只要它有效就行

• 决定下一步生成哪个\(x\in S\)的规则
• 不保证找到的最佳解决方案是全局最优的
• 运行时间不受限制

进化计算和邻域搜索

许多启发式方法将邻域结构强加于集合S，这种启发式方法可以保证找到的最佳点是局部最优的，例如爬山算法，通常很快就能找到好的解决方案。但是，问题往往表现出许多局部最优。

进化算法的特点是：

• 使用种群
• 使用多个随机搜索运算符
• 尤其是元数大于1的变异算子
• 随机选择

提问：进化算法中的邻域是什么？

ChatGPT：与给定解在搜索空间中密切相关或相似的一组潜在解，基于对当前解进行微小修改，即使用突变、杂交或专门的局部搜索可以探索的解。（我觉得很有道理）

表示、突变和重组

最常见的基因组表示：

• 二进制
• 整数
• 实值或浮点数
• 排列
• 树

构建进化算法的第一阶段也是最困难的阶段：为问题选择正确的表示

变异算子：突变和交叉，所需变异算子的类型取决于所选的表示形式

二进制表示

最早的表示方法之一，基因型由一串二进制数字组成

变异：以概率\(p_m\)独立改变每个基因，\(p_m\)称为突变率，通常在\(\frac1{种群大小}\)和\(\frac1{染色体长度}\)之间。变异可引起可变效应（使用格雷码）。

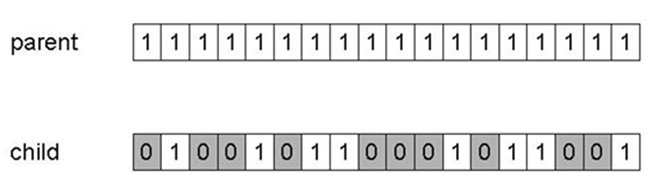Mutation

单点交叉：在两个父母身上随机选择一个点，在这个交叉点上将父母基因拆分，通过交换尾部来创造后代，交叉概率\(P_c\)通常在\((0.6, 0.9)\)范围内。

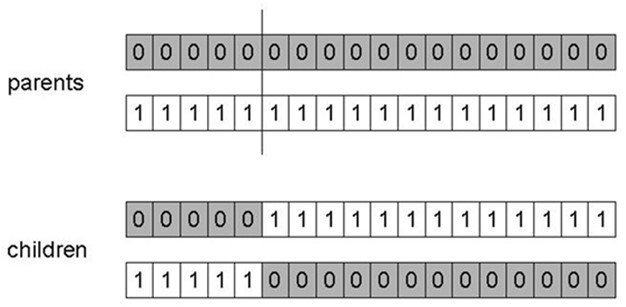1-point crossover

单点交叉的性能取决于变量在表示中出现的顺序，更有可能将彼此靠近的基因放在一起，永远无法将来自基因串两端的基因放在一起，这被称为位置偏差（Position Bias）

n点交叉：选择n个随机交叉点，沿着这些点分割，粘合每个部件，在父母基因之间交替（仍然存在一些位置偏差）。

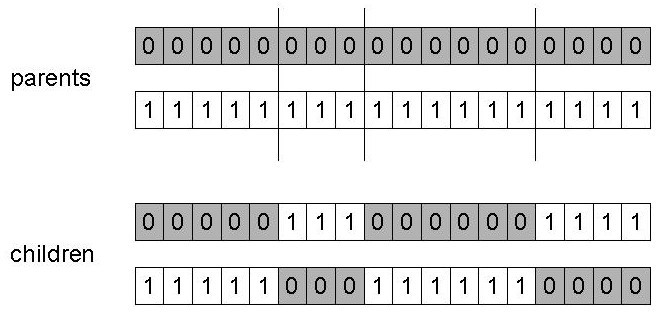n-point crossover

均匀交叉：第一个孩子的每个基因随机从某一个父母选取，第二个孩子从另一个父母的基因选取。

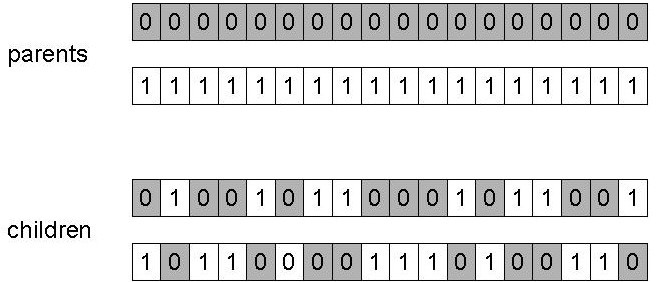uniform crossover

交叉or突变：这取决于具体问题，但一般来说，两者兼有是好的，两者都有各自的作用。仅突变是可行的，但仅交叉不行。

探索：在搜索空间中发现有希望的区域，即获取有关问题的信息。交叉是探索性的，它会大步跃进到两个父母区域“之间”的某个区域。

开发：在有前景的领域内进行优化，即利用信息。突变是开发性的，它会产生随机的小变化，从而保持在父母附近/在父母的范围。

只有交叉才能结合来自两个父母的信息，只有突变才能引入新的信息（等位基因）。交叉不会改变种群的等位基因频率，为了达到最佳效果，通常需要一个“幸运”的突变。

---

Hexo的Markdown渲染好怪…