遗传算法3
接上一篇
表示、突变和重组
整数表示
如今,人们普遍认为直接使用数值变量(整数、浮点变量)进行编码更好。有些问题自然有整数变量,例如图像处理参数,其他颜色则从固定集合中取分类值,例如\({蓝色、绿色、黄色、粉色}\)。
重组与二进制表示相同。N点/均匀交叉算子仍然有效,位翻转突变可以扩展:“蔓延”,即更有可能变为近似值,以概率\(p\)为每个基因添加一个小值(正值或负值);随机重置(尤其是分类变量),以概率\(p_m\)随机选择一个新值。
实数值或浮点数值表示
许多问题都是实值问题,例如连续参数优化\(f:\mathfrak{R}^n\rightarrow\mathfrak{R}\)。
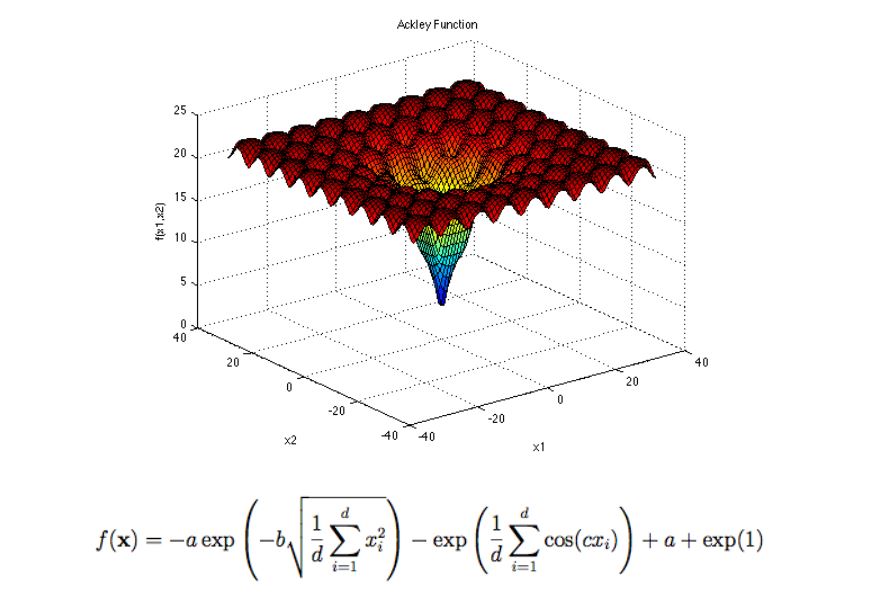
\[f(x,y)=-20\exp \left[-0.2{\sqrt {0.5(x^{2}+y^{2})}}\,\right]{}-\exp \left[0.5\left(\cos 2\pi x+\cos 2\pi y\right)\right]+e+20\]
将实数值映射到位串上
\(z\in[x,y]\subseteq\mathfrak{R}\)表示为\(\{a_1,\cdots,a_L\}\in\{0,1\}^L\)
\([x, y]\rightarrow\{0,1\}^L\)必须是可逆的(每个基因型一个表现型)
\(\Gamma:\{0,1\}^L\rightarrow[x, y]\)定义表示:
\[\Gamma(a_1,\cdots,a_L)=x+\frac{y-x}{2^L-1}\cdot\left(\sum_{j=0}^{L-1}a_{L-j}\cdot2^j\right)\in[x, y]\]
个人解释:第一项\(x\)表示\([x, y]\)的最小值\(x\),\(y-x\)为区间长度。\(2^L-1\)为区间划分数量,即将区间\([x, y]\)划分为\(2^L\)段,每一段可以使用整数序号表示,后面括号中的求和则是根据该序号的二进制表示查询其在\([x, y]\)区间的位置。
因此,这个表示仅能表示\([x, y]\)中无限实数中的\(2^L\)个。L为序号的最大二进制位数长度(染色体长度),决定解决方案的最大可能精度。精度越高,染色体越长,进化速度也越慢。
变异操作
均匀变异
浮点突变的一般方案:\(\bar x=\langle x_1,\cdots,x_L\rangle\rightarrow\bar x'=\langle x_1',\cdots,x_L'\rangle\),其中\(\bar x,\bar x'\in[LB_i,UB_i]\)
chatGPT解释:\(LB_i\)(Lower Bound),\(UB_i\)(Upper Bound)分别为浮点数表示\(x_i\)能取得的最小和最大值。在均匀变异的操作中,新的变量\(x_i'\)将会从范围\([LB_i,UB_i]\)内均匀随机选择。
类似于位翻转(二进制)或随机重置(整数)
非均匀变异
提出了许多方法,例如随时间变化的范围等。大多数方案都是概率性的,但通常只会对值产生很小的改变。最常见的方法是将服从\(N(0,\sigma)\)正态分布的随机偏差分别添加到每个变量中,即\(x_i'=x_i+N(0,\sigma)\)。\(\sigma\)也是变异步长。
自适应变异
步长包含在基因组中,并且本身会经历变异和选择:\(\langle x_1,\cdots,x_n,\sigma\rangle\)。变异步长不由用户设置,而是与解决方案共同进化。在进化搜索过程的不同阶段可能适用不同的变异策略。
变异策略:
- 首先变异\(\sigma\)
- 净突变效应:\(\langle x, \sigma\rangle\rightarrow\langle x', \sigma'\rangle\)
- 顺序很重要:
- 首先\(\sigma\rightarrow\sigma'\)
- 然后\(x'=x+N(0,\sigma')\)
- 理由:新的\(\langle x',
\sigma'\rangle\)会经历2次评估
- 首要原则:如果\(f(x’)\)好,则\(x’\)好
- 次要原则:如果\(x'\)好,那么创造它的\(\sigma'\)好
- 逆转突变顺序是行不通的
交叉操作
分散:
- 后代\(z\)中的每个等位基因值以相等的概率来自其父母\((x,y)\)之一:\(z_i = x_i \text{ or } y_i\)
- 可以使用n点交叉或均匀交叉
折中:
- 利用父母之间创造孩子的想法(因此又称为算术重组)
- \(z_i=\alpha x_i+(1-\alpha)y_i\),其中\(0\leq\alpha\leq1\)
- 其中参数\(\alpha\)可以是
- 常数:均匀算术交叉
- 变量(例如取决于人口年龄)
- 每次随机挑选
单算术交叉
- 父母\(\langle x_1,\cdots,x_n\rangle\)和\(\langle y_1,\cdots,y_n\rangle\)
- 随机选择一个基因\(k\)
- 则\(\text{child}_1=\langle x_1,\cdots,x_{k_1},\alpha y_k+(1-\alpha)x_k,\cdots,x_n\rangle\)
- 为\(\text{child}_2\)做相反的操作,例如当\(\alpha=0.5\)时

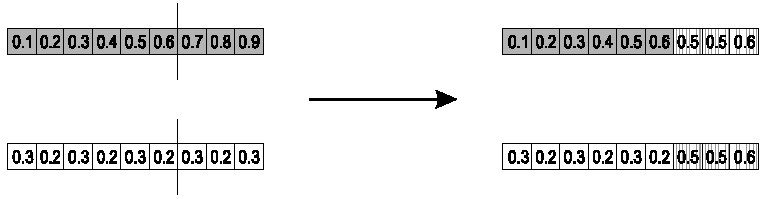
简单算数交叉
- 父母\(\langle x_1,\cdots,x_n\rangle\)和\(\langle y_1,\cdots,y_n\rangle\)
- 随机选择一个基因\(k\),它之后的基因进行混合
- \(\text{child}_1=\langle x_1,\cdots,x_k,\alpha y_{k+1}+(1-\alpha)x_{k+1},\cdots,\alpha y_n+(1-\alpha)x_n\rangle\)
- 为\(\text{child}_2\)做相反的操作,例如当\(\alpha=0.5\)时
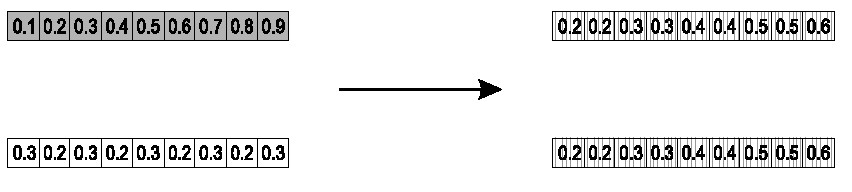
全算术交叉
- 最常用
- 父母\(\langle x_1,\cdots,x_n\rangle\)和\(\langle y_1,\cdots,y_n\rangle\)
- \(\text{child}_1=\alpha\bar y+(1-\alpha)\bar x\)
- 为\(\text{child}_2\)做相反的操作,例如当\(\alpha=0.5\)时
混合交叉
- 父母\(\langle x_1,\cdots,x_n\rangle\)和\(\langle y_1,\cdots,y_n\rangle\)
- 假设\(x_i\le y_i\)
- \(d_i=y_i-x_i\)
- 随机样本\(z_i=[x_i-\alpha d_i, x_i+\alpha d_i]\)
- 原作者的最佳结果是\(\alpha=0.5\)
概述不同的可能后代
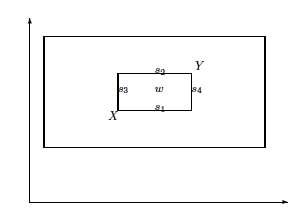
- 单算术:\(\{s_1,s_2,s_3,s_4\}\)
- 简单算术&全算数:内框(\(w\)为\(\alpha=0.5\))
- 混合:外框
多亲本重组
遗传算法不受自然实际情况的限制,突变使用\(n=1\)亲本,而“传统”交叉使用\(n=2\),因此扩展到\(n\gt2\) 是合理的。此法自20世纪60年代以来就已存在,至今仍然罕见,但研究表明有用。
多亲本重组1型
- 想法:分割并重组父母
- 例如:\(n\)个父母的对角交叉
- 选择\(n-1\)个交叉点(每个父母相同)
- 沿着“对角线”将父母的部分组合成\(n\)个孩子
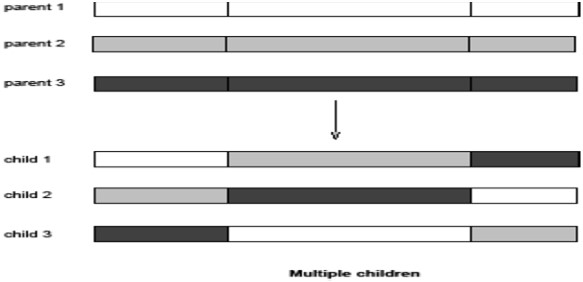
该操作包括了单点交叉
多亲本重组2型
- 想法:等位基因(实值)的算术组合
- 例如:\(n\)个父母的算术交叉:
- 孩子的第\(i\)个等位基因是所有父母第\(i\)个等位基因的平均值
- 在遗传算法中很奇特,长期以来在进化策略中被人们所知和使用
排列表示
任务是(或可以通过)按特定顺序排列一些物体
- 例子:生产调度:重要的是哪些元素被安排在其他元素之前(顺序)
- 例子:旅行商问题(TSP):重要的是哪些元素彼此相邻(邻接)
这些问题通常表示为一种排列:如果有n个变量,则表示为n个整数的列表,每个整数恰好出现一次
先整到这里吧,后面的一部分之后再考虑补不补