图像增强
简单点处理方法
图像处理操作旨在增强图像内容或特征,使其更适合显示或分析。许多图像增强过程都是点和无记忆操作,它们根据变换\(g=T(f)\)将输入图像灰度级映射到输出灰度级。
幂变换伽马校正:\(g=cf^\gamma\)
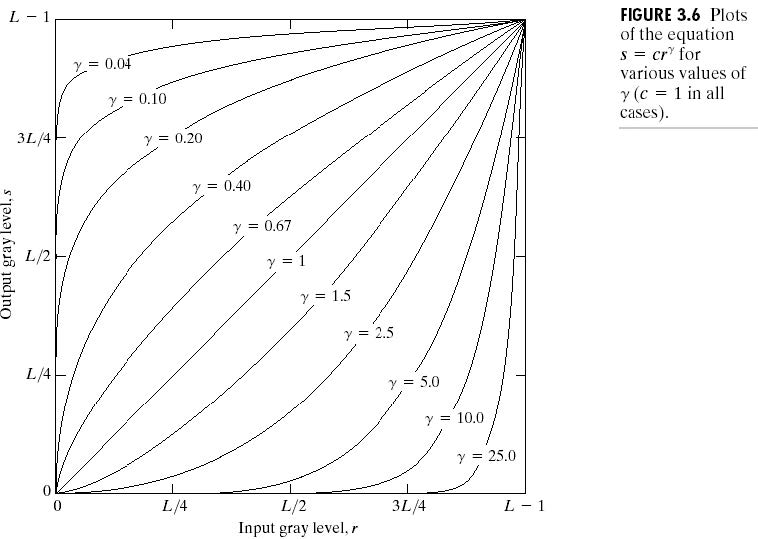
对数变换:\(g=c\log(1+f)\)
分段线性变换:对比度拉伸:
\[\begin{aligned}g&=T(f)\\&=\begin{cases}\alpha f&,0\leq f\lt a\\\beta(f-a)+T(a)&,a\leq f\lt b\\\gamma(f-b)+T(b)&,b\leq f\lt L\end{cases}\end{aligned}\]
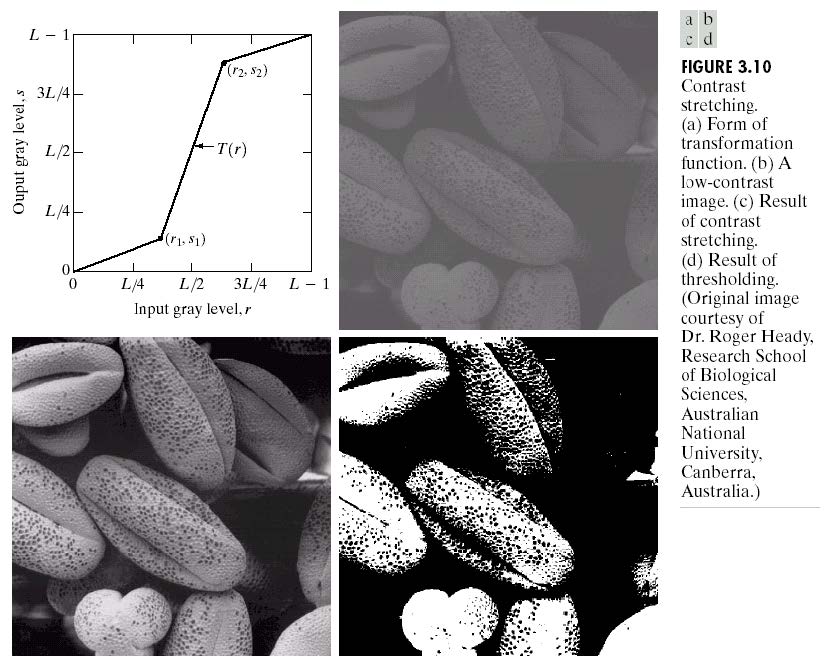
直方图均衡化
直方图均衡化的目的是通过将输入图像\(f(x,y)\)的灰度级\(f\)转换为\(g\),为输出图像\(g(x,y)\)获得均匀的直方图。
直方图均衡算法:
\[c(f)=\sum_{t=0}^fp_f(t)=\sum_{t=0}^f\frac{n_t}n\ ,f=0,1,\cdots,L\]
\[g=T(f)=\left[\frac{c(f)-c_{\min}}{1-c_{\min}}L\right]\ ,c(f)\geq c_{\min}\]
其中\(c_{\min}\)是获得的所有\(c(f)\)中的最小正值,方括号\([]\)将实数四舍五入为整数。\(g\)在\([0,L]\)中近似均匀分布。
直方图均衡化的理论分析只能针对连续变量进行,令\(f\)为连续灰度值,归一化至\([0,1]\),令变换\(g=T(f)\)为单值,在\(0\leq g=T(f)\leq1\)中单调递增,则逆变换为$f=T{-1}(g)也应该是单值且单调递增的。
根据概率论,如果已知原始灰度概率分布函数\(p_f(f)\)和\(T(f)\),且\(T^{-1}(g)\)满足上述条件,则变换后的灰度概率分布函数\(p_g(g)\)为
\[p_g(g)=p_f(f)\frac{\text df}{\text dg}\]
考虑\(g=T(f)=\int_0^fp_f(t)\text dt\),此函数是\(f\)的累积分布函数(cdf)。cdf是单值且单调递增的。
因为\(\frac{\text df}{\text dg}=\frac1{p_f(f)}\),所以\(p_g(g)=p_f(f)\frac{\text df}{\text dg}=p_f(f)\frac1{p_f(f)}=1\),因此,变换后的灰度值具有均匀分布。
直方图均衡化\(c(f)=\sum_{t=0}^fp_f(t)=\sum_{t=0}^f\frac{n_t}n\)就是离散版本的\(g=T(f)=\int_0^fp_f(t)\text dt\)
图像平滑
空间和频率域中的线性图像滤波的基本形式可以表示为
\[\begin{aligned}G(u,v)&=F(u,v)H(u,v)\\g(x,y)&=f(x,y)*h(x,y)\\&=\sum_{j=-\infty}^{+\infty}\sum_{i=-\infty}^{+\infty}h(i,j)f(x-i,y-j)\\&=\sum_{j=-3}^3\sum_{i=-3}^3h(i,j)f(x-i,y-j)\ ,\text{if}\ h(x,y)=0\ \text{for}\ -3\lt x,y\lt3\end{aligned}\]
在每个点\((x,y)\)处,该点的滤波器响应为:滤波器系数与以\((x,y)\)为中心的滤波器掩模所跨越的区域中相应图像像素的乘积之和。
图像平滑滤波器用于模糊和降低噪音,这些滤波器也称为平均滤波器或低通滤波器。
低通滤波(Low-Pass Filter, LPF)是图像处理领域中的一种基础技术,旨在让图像中的低频信号通过,同时削弱或抑制高频信号。换句话说,低通滤波器专注于保留图像的大体轮廓和色彩,而减弱或去除其中的噪声和细节。
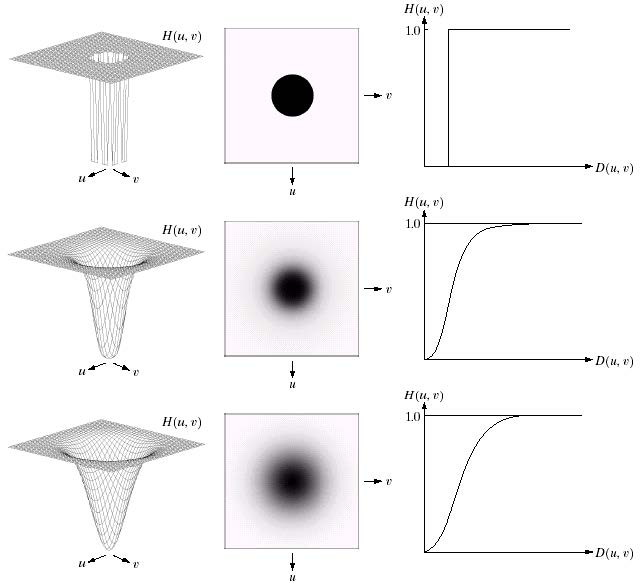
理想低通滤波:
\[\begin{aligned}D(u,v)&=\sqrt{u^2+v^2}\\H(u,v)&=\begin{cases}1&,D(u,v)\leq D_0\\0,&,D(u,v)\gt D_0\end{cases}\end{aligned}\]
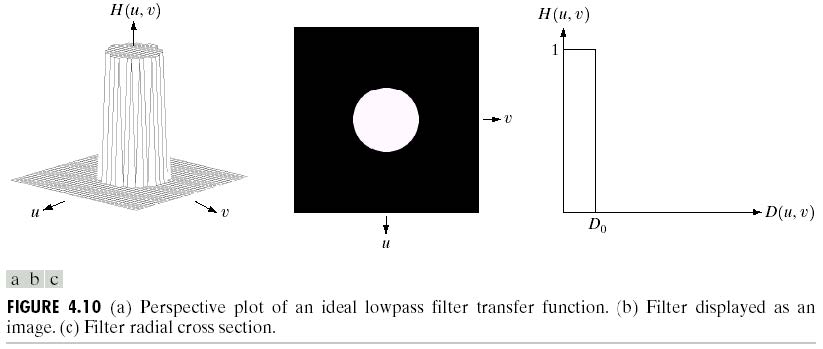
高斯低通滤波(GLPF):
\[G(u,v)=\frac1{2\pi\sigma^2}\text e^{-\frac{u^2+v^2}{2D_0}}\]
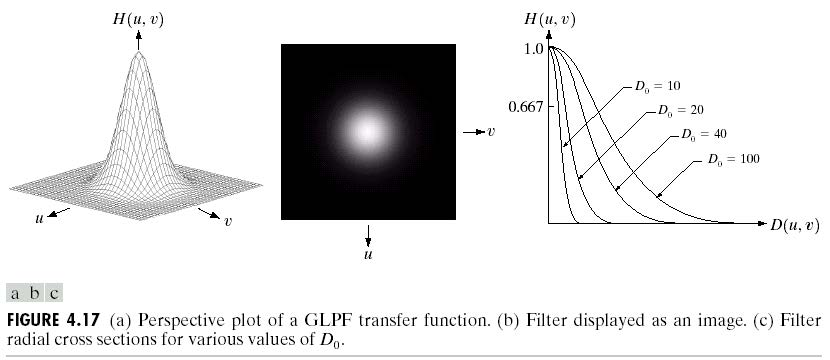
图像锐化
高通滤波:
\[H_{hp}(u,v)=1-H_{lr}(u,v)\]
理想高通滤波:
\[\begin{aligned}D(u,v)&=\sqrt{u^2+v^2}\\H(u,v)&=\begin{cases}0&,D(u,v)\leq D_0\\1,&,D(u,v)\gt D_0\end{cases}\end{aligned}\]
高斯高通滤波(GHPF):
\[G(u,v)=1-\text e^{-\frac{u^2+v^2}{2D_0}}\]
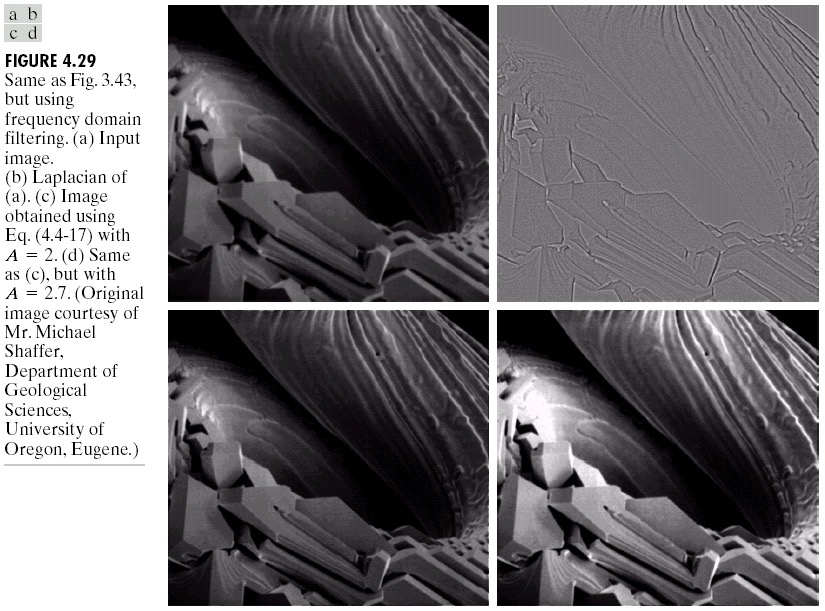
高提升滤波:
\[f_{hb}(x,y)=Af(x,y)-f_{lp}(x,y)\]
其中\(f_{lp}(x,y)\)是经过低通滤波器平滑后的\(f(x,y)\),\(A\geq1\)
非线性图像处理
线性滤波器的问题
任何线性滤波器的输出都是输入像素的加权平均值
\[\begin{aligned}\hat f(x,y)&=h(x,y)*f(x,y)\\&=\sum_{i=-a}^a\sum_{j=-b}^bh(i,j)f(x-i,y-j)\\&=\sum_{(s,t)\in S_{xy}}\omega(s,t)f(s,t)\end{aligned}\]
图像模糊,清晰度细节丢失,难以平滑强噪点
顺序统计滤波器
该滤波器的响应基于对滤波器所涵盖的图像区域内的像素的排序(排列)。最著名的例子是中值滤波器,它用像素邻域内灰度级的中值替换像素的值。
\[\hat f(x,y)=\text{median}_{(s,t)\in S_{xy}}\{f(s,t)\}\]

考虑具有脉冲函数的均匀一维图像,脉冲函数对应线条、曲线等精细的图像细节。
均值滤波器使图像细节“模糊”。如果脉冲是噪声,平均滤波器只能在一定程度上抑制它,但会扩散噪声。
中值滤波器不会“模糊”边缘。如果脉冲是噪声,\(5\times5\)中值滤波器可以完全去除这种噪声。
边缘是图像的基本且重要的结构。均值滤波器对于衰减脉冲噪声无效并且会使边缘模糊。而中值滤波器具有出色的降噪能力并保留边缘。均值滤波器可衰减加性高斯噪声,但会使边缘模糊。中值滤波器可衰减高斯噪声并保留边缘。
中值滤波器强制具有不同灰度级的点更像它们的相邻像素。相对于相邻像素而言更亮或更暗且面积小于\(\frac{n^2}2\)(滤波器面积的一半)的孤立像素簇将被\(n\times n\)中值滤波器消除。消除=强制使值等于邻居的中值强度。较大的簇受到的影响要小得多。
线性滤波器已经建立了理论来分析其特性,特别是在频域中。然而,中值滤波器和其他顺序统计滤波器由于其非线性特性,使其分析起来很困难。对信号重复应用中值滤波器会产生一个称为“根信号”的不变信号。根信号对于进一步应用中值滤波器而言是不变的。
中值滤波器的简单扩展:
- 最大滤波器:\[\hat f(x,y)=\max_{(s,t)\in S_{xy}}\{f(s,t)\}\]
- 最小滤波器:\[\hat f(x,y)=\min_{(s,t)\in S_{xy}}\{f(s,t)\}\]
- 中点滤波器:\[\hat f(x,y)=\frac12\left[\max_{(s,t)\in S_{xy}}\{f(s,t)\}+\min_{(s,t)\in S_{xy}}\{f(s,t)\}\right]\]
虽然中值滤波器保留了图像边缘,但它会删除图像细节,例如角落,细线/曲线和其他精细细节。
由于中值滤波器在衰减短尾噪声(例如高斯噪声)方面的表现不如均值滤波器,因此已经开发出兼具均值滤波器和中值滤波器优点的滤波器:
修正阿尔法均值滤波器(Alpha-trimmed mean filter):
\[\hat f(x,y)=\frac1{mn-d}\sum_{(s,t)\in S_{xy}}f_r(s,t)\]
其中\(f_r(s,t)\)是中位数周围剩余的\(mn-d\)个像素
前面还好,后面又有点依托。
后面还有依托Iterative Truncated Arithmetic Mean Filter,好像是老师以前的研究,还好不考……