形态学图像处理
看图感觉又是依托大的,但是经典机器视觉最后一章了,忍忍罢。
绪论

对于上图,图像的灰度值并不重要,因为只有两个不同的灰度值。但是,区域形状和物体的边界很重要。
这样的二值图像可以用对象像素集来表示
\[A=\{a|a=(x,y),f(x,y)=1\}\]
形态学研究形式和结构,数学形态学是一种提取图像成分的工具,其用途如下:
- 区域形状的表示和描述(例如边界)
- 预处理或后处理(过滤、细化等)
形态学操作基于集合论和逻辑运算,是图像分析的有力工具。它们通常对二值图像进行操作,因此经常用于分割任务或边缘检测任务。
集合论与逻辑运算
二维整数集表示为\(\mathbf Z^2\),此空间中的一个元素有两个组成部分\(a=(a_1,a_2)\)。对于图像表示,\(a=(a_1,a_2)\)是像素的\(x\)和\(y\)坐标。
令\(A\)为\(\mathbf Z^2\)中的一个子集。若\(a=(a_1,a_2)\)为\(A\)中的一个元素,则我们表示
\[a\in A\]
否则
\[a\notin A\]
\(\emptyset\)表示空集。
如果集合\(A\)是\(B\)的子集,我们表示
\[A\subseteq B\]
集合运算:
- 并集:\(C=A\cup B\)
- 交集:\(C=A\cap B\)
- 不相交的集:\(A\cap B=\emptyset\)
- 补集:\(A^\text C=\{w|w\notin A,w\in\mathbf Z^2\}\)
- 集合减法:\(A-B={w|w\in A,w\notin B}=A\cap B^\text C\)
- 集合平移:\((A)_z=\{c|c=a+z,a\in A\}\ ,z=(z_1,z_2)\)
- 集合反射(关于原点对称):\(\hat B=\{w|w=-b,b\in B\}\)
形态学操作
形态学操作最主要的是膨胀和腐蚀,可以通过结合腐蚀和膨胀来设计更复杂的形态学算子,例如开运算和闭运算。开运算通常会使图像的轮廓变得平滑,并消除凸起;闭运算使轮廓的各个部分变得平滑,但通常会融合断裂、孔洞和间隙。
膨胀和腐蚀
膨胀
用\(B\)使\(A\)膨胀,记为\(A\oplus B\),定义为:
\[A\oplus B=\left\{\begin{array}{c|r}z&\left[\left(\hat B\right)_z\cap A\right]\neq\emptyset\end{array} \right\}\]
解释: 获取\(B\)绕其原点的反射,然后将该反射平移\(z\)。\(A\)被\(B\)膨胀后,就是所有使得平移后的\(B\)和\(A\)至少有一个非零元素重叠的\(z\)位移的集合。
\(B\)在膨胀中被称为结构元素。
进一步解释: 集合\(B\)可以看作是一个卷积掩码。“翻转”\(B\)然后依次移动它,使其滑过集合\(A\)的基本过程类似于卷积。

腐蚀
用\(B\)使\(A\)腐蚀,记为\(A\ominus B\),定义为:
\[A\ominus B=\left\{\begin{array}{c|r}z&\left[(B)_z\cap A\right]\subseteq A\end{array} \right\}\]
\(A\)被\(B\)侵蚀是所有点\(z\)的集合,使得\(B\)经过\(z\)平移后包含在\(A\)中。
膨胀和腐蚀在集合补集和反射方面互为对偶。也就是说,
\[(A\ominus B)^\text C=A^\text C\oplus\hat B\]
开闭运算
开运算
复合运算是指连续执行两个或多个形态学运算。一个常见的例子是开运算,即先腐蚀,然后膨胀:
\[A\circ B=(A\ominus B)\oplus B\]
通过对所有大小适合\(A\)的\(B\)平移进行并集,可以得到\(A\)以\(B\)的开。这可以表示为如下拟合处理:
\[A\circ B=\bigcup\{(B)_z|(B)_z\subseteq A\}\]
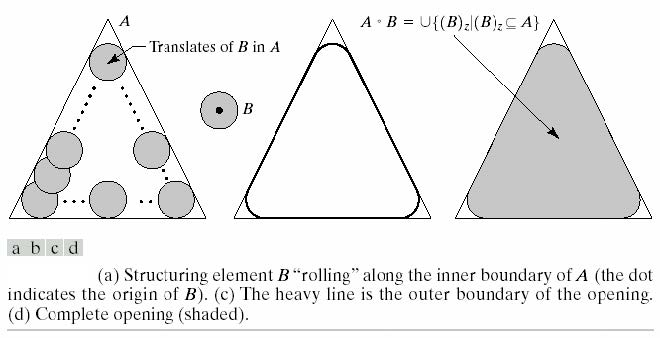
向外指向的角会变圆,而向内指向的角保持不变。
开运算通常用于清除图像中的噪声,同时保留原始物体的大小。如果噪声很大,则必须注意操作不会扭曲物体的形状大小。开运算往往会使物体上尖锐的半岛形状突起变得平坦。查看开运算效果的一个有用方法是通过将这些差异投影到原始图像上来寻找原始图像和开运算后的图像之间的差异。
闭运算
闭运算是开运算的互补运算,定义为先膨胀,然后腐蚀:
\[A\bullet B=(A\oplus B)\ominus B\]
开运算和闭运算互为对偶,即:
\[(A\bullet B)^\text C=A^\text C\circ\hat B\]
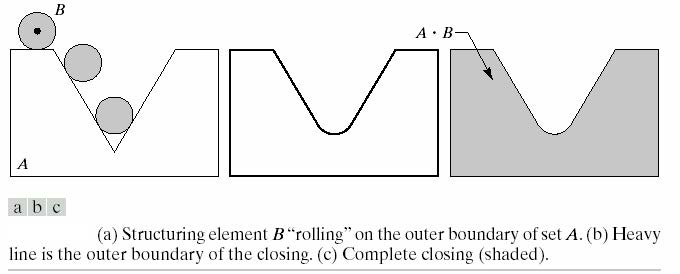
向内指向的角会变圆,而向外指向的角保持不变。
闭运算的经典应用是填补区域中的空洞,同时保留原始对象的大小。膨胀会填补空洞,而腐蚀会恢复原始区域大小。除了填补洞之外,闭运算还会填充区域边缘的“隔间”。
开和闭运算
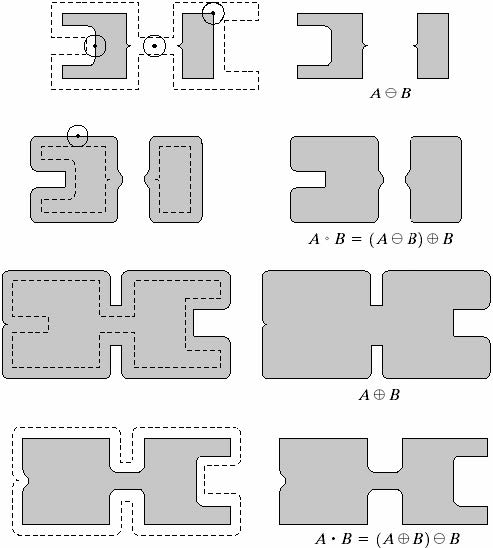
开运算满足以下性质:
- \(A\circ B\subseteq A\)
- 若\(C\subseteq D\),则\(C\circ B\subseteq D\circ B\)
- \((A\circ B)\circ B=A\circ B\)
类似地,闭运算满足以下性质:
- \(A\subseteq A\bullet B\)
- 若\(C\subseteq D\),则\(C\bullet B\subseteq D\bullet B\)
- \((A\bullet B)\bullet B=A\bullet B\)
形态学算法及应用
边界提取
集合\(A\)的边界用\(\beta(A)\)表示,可以通过以下方式获得:
\[\beta(A)=A-(A\ominus B)\]
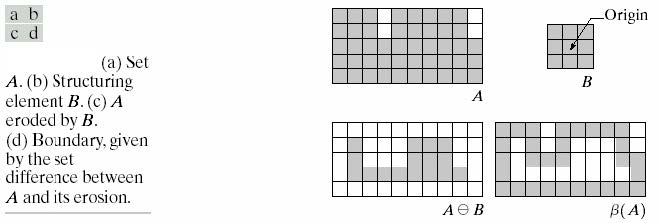
区域填充
\[X_k=(X_{k-1}\oplus B)\cap A^\text C\]
\[A^F=X_k\cup A\]
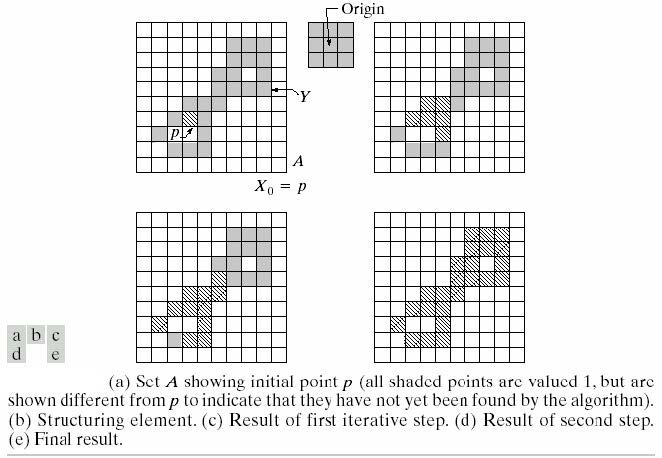
从边界内的点\(X_0\)开始,通过上述过程填充边界内的整个区域。
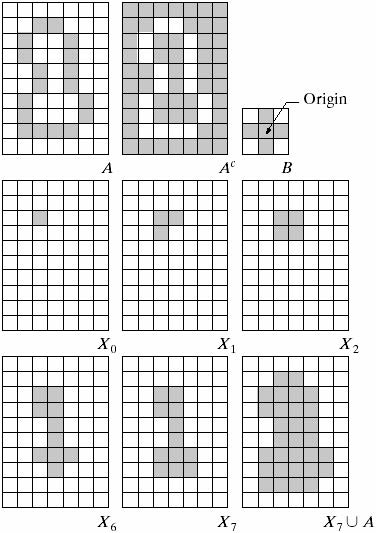
提取连通分量
\[X_k=(X_{k-1}\oplus B)\cap A\]
去噪
\[(A\circ B)\bullet B\]
或
\[(A\bullet B)\circ B\]
可用于消除噪声及其对物体的影响。
使用\(B\)开运算去除物体区域外的噪声像素,使用\(B\)闭运算去除物体区域内的噪声像素。

终于啃完了,还是比较简单,重点是不抽象了,实际运用都能想象出来,希望后面简单些吧(
好饿,该吃饭了。