图像压缩和JPEG标准

发表于 2024-09-02 更新于 2024-09-11

讲解了JPEG图像压缩的原理，包括离散余弦变换（DCT）、Huffman编码等。

术语和概念

压缩/编码：减少表示某些信息所需的总bit数

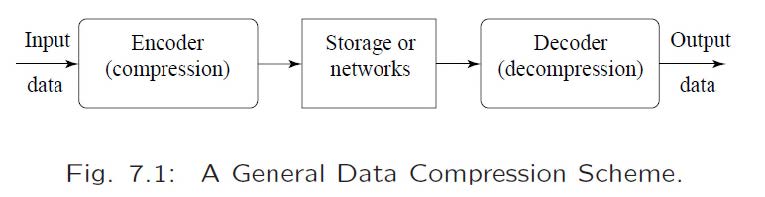
压缩比：指示数据压缩程度的指标

\[压缩比=\frac{\text{压缩前的bit数}B_0}{\text{压缩后的bit数}B_1}\]

信息论基础：字母表\(S=\{s_1,s_2,\cdots,s_n\}\)的信息源的熵\(\mu\)为：

\[\begin{aligned}\mu=H(S)&=\sum_{i=1}^np_i\lg\frac1{p_i}\\&=-\sum_{i=1}^np_i\lg p_i\end{aligned}\]

\(p_i\)：符号\(s_i\)在\(S\)中出现的概率

熵编码

Huffman编码

一种可变长度编码（Variable Length Coding，VLC），较高频率的模式（符号）被分配较短的代码字，从而使用于表示每个模式/符号的平均位数减少

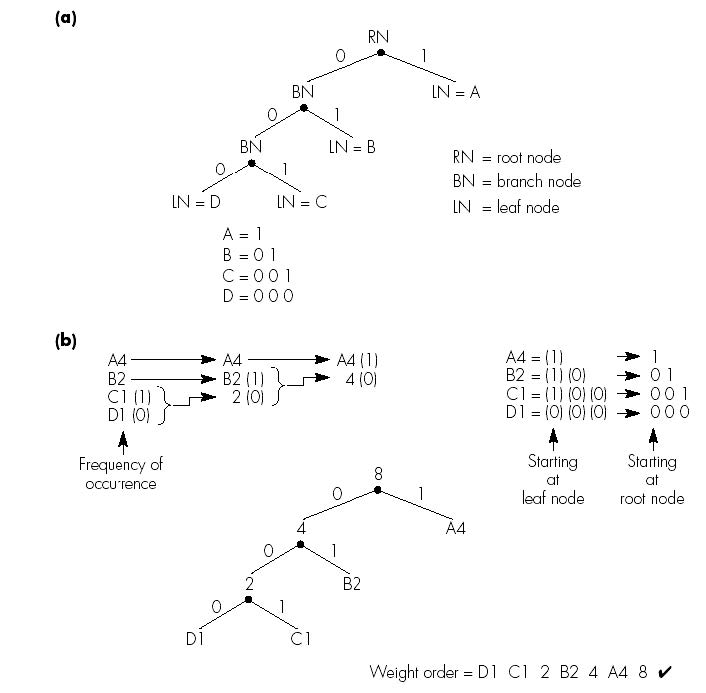
Huffman编码树是一棵二叉树，其分支分配有值0或1。

树结构：

根节点：树的根
分支节点：分支的分叉点
叶节点：分支的终止点

在每个分支节点处，分别将0和1分配给左分支和右分支，通过追踪从根节点到叶节点的路径来确定每个字符/符号使用的代码字

练习：Huffman编码\(1\)

在压缩方案中，\(8\)个符号用于表示信息源中的不同模式。这些符号使用码本\(A\)的码字进行编码。码本\(A\)和发生概率如下表所示，其中\(m\)和\(n\)为正实数。

符号	\(s_0\)	\(s_1\)	\(s_2\)	\(s_3\)	\(s_4\)	\(s_5\)	\(s_6\)	\(s_7\)
出现概率	\(m\)	\(n\)	\(0.15\)	\(0.10\)	\(0.08\)	\(0.06\)	\(0.05\)	\(0.02\)
码本\(A\)中的码字	`01`	`111`	`110`	`101`	`100`	`001`	`0001`	`0000`

\(a)\)

在第一种情况下，如果压缩方案的平均位数/符号需要小于\(2.86\)，请找出\(m\)和\(n\)值所需的条件。

由题可得：

\[\begin{cases}\sum_{i=0}^7\text{length}(\text{codeword}_i)p_i\lt2.86\\\sum_{i=0}^7p_i=1\end{cases}\]

则有

\[\begin{aligned}&2m+3n+0.15\times3+0.10\times3+0.08\times3+0.06\times3+0.05\times4+0.02\times4\\=&2m+3n+1.45\\\Rightarrow&2m+3n<1.41\end{aligned}\]

以及

\[\begin{aligned}m+n+0.15+0.10+0.08+0.06+0.05+0.02&=1\\m+n+0.46&=1\\m+n&=0.54\\m&=0.54-n\end{aligned}\]

带入不等式，得

\[\begin{aligned}2\times0.54+n&\lt1.41\\n&\lt0.33\end{aligned}\]

则

\[\begin{cases}m\gt0.21\\n\lt0.33\end{cases}\]

\(b)\)

在第二种情况下，如果\(m=0.30\)且\(n=0.24\)，讨论码本\(A\)在编码符号以实现压缩方面的有效性。将码本\(A\)与Huffman编码进行比较，讨论码本\(A\)在这种情况下执行压缩是否是最佳的。

由题，建立以下Huffman树（数字为\(s_i\)的下标，B为分支点，R为根）：

       R
      / \
     /   \     
    B     B
   / \   / \
  B   1 B   0
 / \   / \
4   3 B   2
     / \
    5   B
       / \
      7   6

则该Huffman编码的码本如下

符号	\(s_0\)	\(s_1\)	\(s_2\)	\(s_3\)	\(s_4\)	\(s_5\)	\(s_6\)	\(s_7\)
码字	`11`	`01`	`101`	`001`	`000`	`1000`	`10011`	`10010`

则其平均位数/符号为

\[0.30\times2+0.24\times2+0.15\times3+0.10\times3+0.08\times3+0.06\times4+0.05\times5+0.02\times5=2.66\]

而题目中所给的方案的平均\(\text{bits/symbol}\)

\[0.30\times2+0.24\times3+0.15\times3+0.10\times3+0.08\times3+0.06\times3+0.05\times4+0.02\times4=2.77\]

由于\(2.77>2.66\)，因此Huffman编码的压缩比高于码本\(A\)，码本\(A\)的方案并不是最佳的。

练习：Huffman编码\(2\)

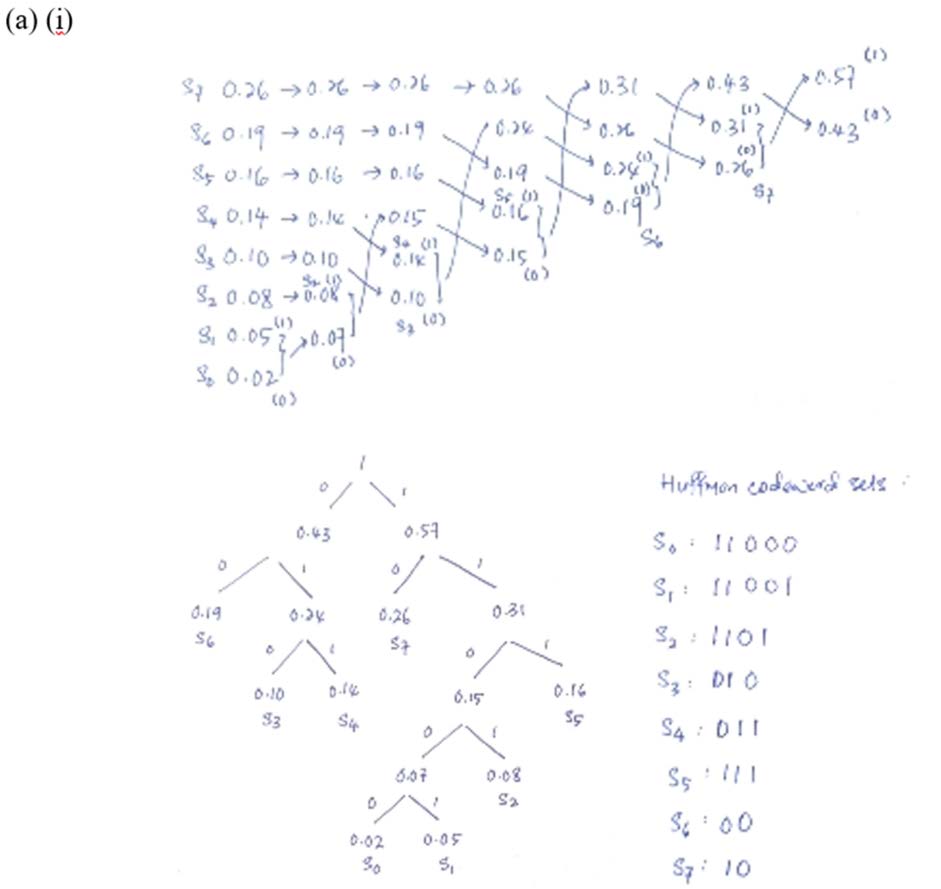
在压缩方案中，数据源由\(8\)个符号组成，其概率分布如表所示。

符号	\(s_0\)	\(s_1\)	\(s_2\)	\(s_3\)	\(s_4\)	\(s_5\)	\(s_6\)	\(s_7\)
出现概率	\(0.02\)	\(0.05\)	\(0.08\)	\(0.10\)	\(0.14\)	\(0.16\)	\(0.19\)	\(0.26\)

\((ⅰ)\)

为这\(8\)个符号设计一组合适的Huffman码字。清晰地展示所有关键步骤和计算。

由题，建立以下Huffman树（数字为\(s_i\)的下标，B为分支点，R为根）：

     R
    / \
   /   \
  B     B
 / \   / \
6   B 7   B
   / \   / \
  3   4 B   5
       / \
      B   2
     / \
    0   1

符号	\(s_0\)	\(s_1\)	\(s_2\)	\(s_3\)	\(s_4\)	\(s_5\)	\(s_6\)	\(s_7\)
码字	`11000`	`11001`	`1101`	`010`	`011`	`111`	`00`	`10`

由于Markdown无法写出详细解法，这里把上课老师写的贴出来。

\((ⅱ)\)

一名学生最初使用\(8\)位来表示未压缩方案中的每个符号。与原始未压缩方案相比，找出第\((ⅰ)\)部分中开发的Huffman编码方案的压缩率。

Huffman编码方案的平均\(\text{bits/symbol}\)：

\(0.02\times5+0.05\times5+0.08\times4+0.10\times3+0.14\times3+0.16\times3+0.19\times2+0.26\times2=2.77\)

则压缩比为

\[\frac8{2.77}=2.888\]

\((ⅲ)\)

求出数据源的熵。简要讨论是否有可能设计一个码字集，实现小于2.5位/符号的目标。

\[\begin{aligned}\mu&=-\sum_{i=0}^7p_i\lg p_i\\&=-(0.02\lg0.02+0.05\lg0.05+0.08\lg0.08+0.10\lg0.10+0.14\lg0.14+0.16\lg0.16+0.19\lg0.19+0.26\lg0.26)\\&=2.73332\ \text{bits/symbol}\end{aligned}\]

由于目标\(2.5\ \text{bits/symbol}\)小于熵，因此无法设计满足目标的码字集

图像和视频压缩基础知识

图像/视频压缩是必要的，原因有二：

减少图像/视频的存储要求
降低通过网络传输的比特率要求

图像和视频可以通过两种类型的冗余进行压缩：

统计冗余
- 空间冗余：空间冗余是指图像内（或更具体地说，在小的图像邻域内）像素之间的统计相关性，也被称为帧内冗余
- 时间冗余：时间冗余是指视频序列中连续帧的像素之间的统计相关性，也被称为帧间冗余
- 编码冗余：编码冗余关注的是信息的表示，即编码本身
心理视觉冗余
- 频率掩蔽：人类对高频成分中的噪声或失真不太敏感
- 颜色掩蔽：人类对亮度（luminance）成分比色度（chrominance）成分更敏感

有损和无损压缩：

无损压缩
- 用于重要数据（例如医学图像）
- 解压缩后重建的图像与原始图像完全相同
有损压缩
- 对于图像或视频等媒体，没有必要显示超出人耳或眼睛能够感知的信息
- 压缩技术可能会丢弃人类察觉不到差异的数据
- 解压缩后重建的图像与原始图像并不完全相同

失真测量/指标：

图像压缩中最常用的三种失真测量方法是 1. 均方误差（Mean Squared Error，MSE）：\[\sigma_d^2=\frac1N\sum_{i=1}^N(x_i-y_i)^2\]其中，\(x_i\)、\(y_i\)和\(N\)分别是输入数据序列、重构数据序列和数据序列的长度 2. 信噪比（Signal to Noise Ratio，SNR），以分贝（decibel，dB）为单位：\[\text{SNR}=10\log_{10}\frac{\sigma_x^2}{\sigma_d^2}\]其中\(\sigma_x^2\)是原始数据序列的平均平方值，\(\sigma_d^2\)是MSE 3. 峰值信噪比（Peak Signal to Noise Ratio，PSNR）：\[\text{PSNR}=10\log_{10}\frac{x_\text{peak}^2}{\sigma_d^2}\]

基于变换的编码/压缩

变换编码：将数据转换为更适合压缩的形式，通过应用逆变换可以获得原始信号。

变换能够产生良好的压缩特性：

提供能量压缩
提供冗余减少（即减少变换系数之间的相关性）

典型的基于变换的图像压缩系统包括以下步骤：图像分割、变换、量化和编码

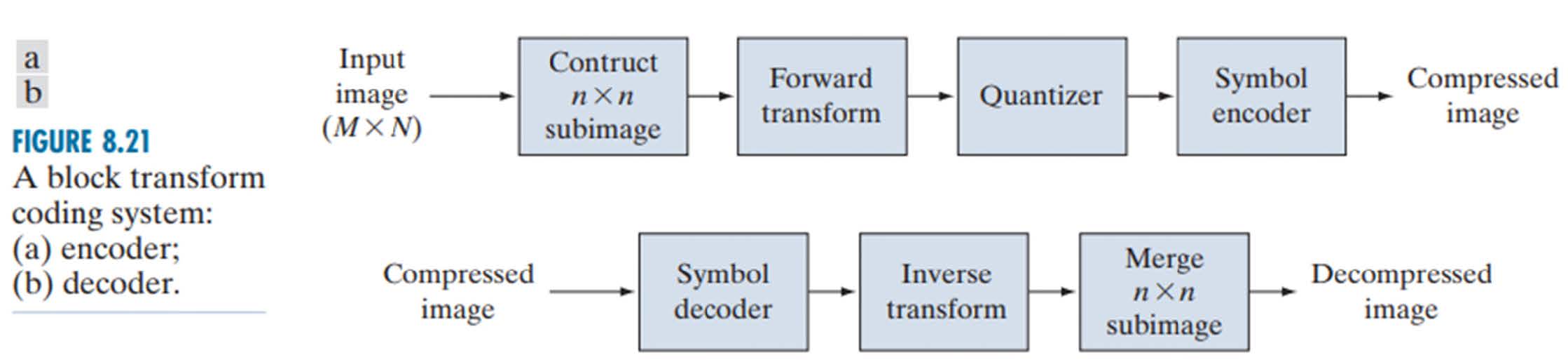
变换：对输入图像数据应用一对一变换，转换后的输出表示形式比原始图像数据更适合有效压缩。

诸如DCT之类的酉映射将信号能量打包成少量的系数。一些主流的变换：

离散傅里叶变换（DFT）
离散余弦变换（DCT）
离散小波变换（DWT）
等等

量化：从变换系数生成有限数量的符号，是不可逆的多对一映射，会导致信息丢失

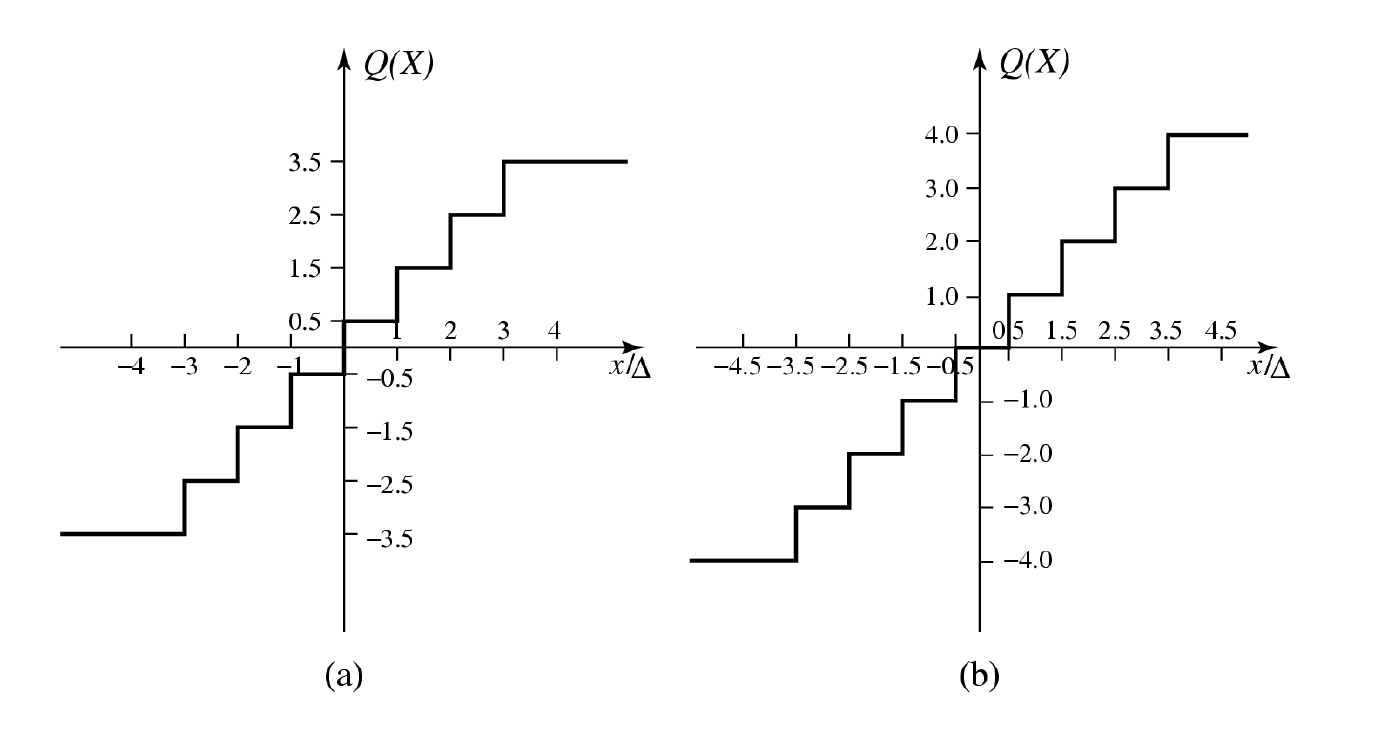
标量量化

编码：在量化器的输出处为每个符号分配一个代码字或二进制比特流，可以采用固定长度或可变长度编码

可变长度编码（VLC）或熵编码以最小化符号二进制表示的平均长度的方式分配码字，这是通过将更短的代码字分配给更可能的符号来实现的，这是熵编码（例如Huffman编码）的基本原理

离散余弦变换（DCT）

关于DCT和量化，看完就懂了：离散余弦变换可视化讲解

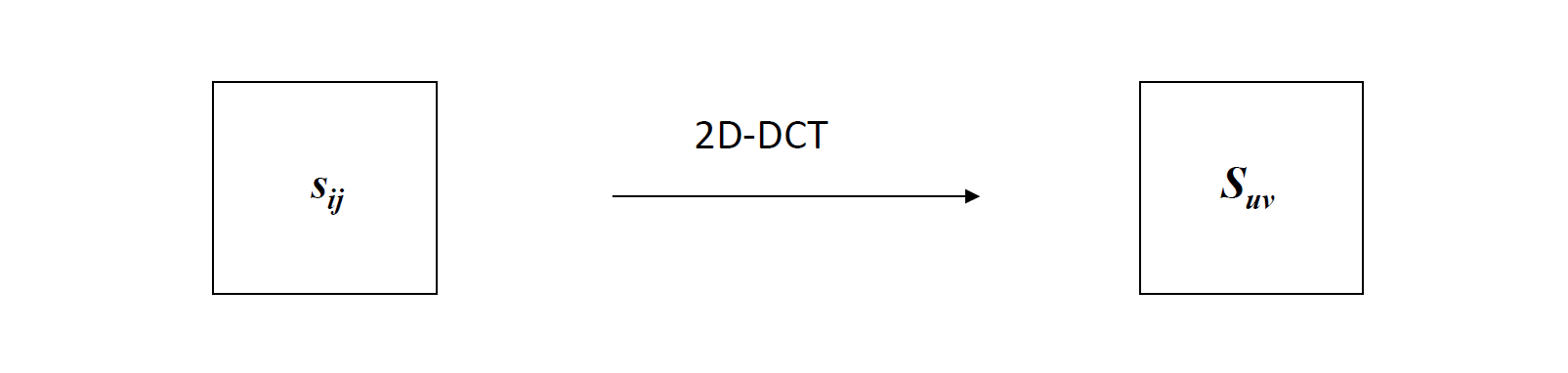
\[S_{uv}=\alpha(u)\alpha(v)\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}s_{ij}\cos\frac{(2i+1)u\pi}{2N}\cos\frac{(2j+1)v\pi}{2N}\qquad u,v=0,1,\cdots,N-1\\\alpha(k)=\begin{cases}\sqrt\frac1N&,k=0\\\sqrt\frac2N&,k=1,2,\cdots,N-1\end{cases}\]

2D-DCT是一种基于变换的图像压缩中常用的变换，它可以提供以下功能：

变换系数的能量压缩
变换系数之间的冗余减少

优点：压缩效果好，基函数固定且不依赖于图像。

缺点：压缩不如其他一些变换那么有效，例如Karhunen–Loève变换。

变换通常可以通过基函数的变化来描述，变换涉及图像信号的视角的改变。基函数类似于“乐高函数”。

练习：2D-DCT \((1)\)

\(N\times N\)数据矩阵的二维离散余弦变换（2D DCT）如下

\[S_{uv}=\alpha(u)\alpha(v)\sum_{i=0}^{N-1}\sum_{j=0}^{N-1}s_{ij}\cos\frac{(2i+1)u\pi}{2N}\cos\frac{(2j+1)v\pi}{2N}\qquad u,v=0,1,\cdots,N-1\]

其中

\[\alpha(k)=\begin{cases}\sqrt\frac1N&,k=0\\\sqrt\frac2N&,k=1,2,\cdots,N-1\end{cases}\]

\((a)\)

计算以下\(4\times4\)像素块\(A\)的2D DCT

\[A=\left[\begin{array}{cccc}0&0&0&0\\0&10&10&0\\0&10&10&0\\0&0&0&0\end{array}\right]\]

~~做个人吧~~

解：

由题，

\[\begin{aligned}S_{uv}&=\alpha(u)\alpha(v)\sum_{i=0}^{3}\sum_{j=0}^{3}s_{ij}\cos\frac{(2i+1)u\pi}{8}\cos\frac{(2j+1)v\pi}{8}\\&=\alpha(u)\sum_{i=0}^{3}\cos\frac{(2i+1)u\pi}{8}\left(\alpha(v)\sum_{j=0}^{3}s_{ij}\cos\frac{(2j+1)v\pi}{8}\right)\end{aligned}\]

令

\[F_{iv}=\alpha(v)\sum_{j=0}^{3}s_{ij}\cos\frac{(2j+1)v\pi}{8}\]

则

\[S_{uv}=\alpha(u)\sum_{i=0}^{3}F_{iv}\cos\frac{(2i+1)u\pi}{8}\]

对于\(i=0\)

\[F_{0v}=\alpha(v)\sum_{j=0}^{3}s_{0j}\cos\frac{(2j+1)v\pi}{8}=0\]

因此

\[F_{0v}=\left[\begin{array}{cccc}0&0&0&0\end{array}\right]\]

对于\(i=1\)

\[F_{1v}=\alpha(v)\sum_{j=0}^{3}s_{1j}\cos\frac{(2j+1)v\pi}{8}\]

由于\(s_{10}=s_{13}=0\)，所以

\[\begin{aligned}F_{1v}&=\alpha(v)\left(s_{11}\cos\frac{3v\pi}{8}+s_{12}\cos\frac{5v\pi}{8}\right)\\&=10\alpha(v)\left(\cos\frac{3v\pi}{8}+\cos\frac{5v\pi}{8}\right)\end{aligned}\]

则

\[\begin{aligned}F_{10}&=10\sqrt\frac14(1+1)=10\\F_{11}&=10\sqrt\frac24\left(\cos\frac{3\pi}{8}+\cos\frac{5\pi}{8}\right)=0\\F_{12}&=10\sqrt\frac24\left(\cos\frac{3\pi}{4}+\cos\frac{5\pi}{4}\right)=\frac{10}{\sqrt2}\cdot-2\sqrt2=-10\\F_{13}&=10\sqrt\frac24\left(\cos\frac{9\pi}{8}+\cos\frac{15\pi}{8}\right)=0\end{aligned}\]

因此

\[F_{1v}=\left[\begin{array}{cccc}10&0&-10&0\end{array}\right]\]

同理可得

\[\begin{aligned}F_{2v}&=\left[\begin{array}{cccc}10&0&-10&0\end{array}\right]\\F_{3v}&=\left[\begin{array}{cccc}0&0&0&0\end{array}\right]\end{aligned}\]

因此，经过1D DCT后

\[F_{iv}=\left[\begin{array}{cccc}0&0&0&0\\10&0&-10&0\\10&0&-10&0\\0&0&0&0\end{array}\right]\]

对\(F_{iv}\)按列进行1D DCT，由于

\[F_{0v}=\left[\begin{array}{c}0\\10\\10\\0\end{array}\right]\]

所以

\[S_{0v}=\left[\begin{array}{c}10\\0\\-10\\0\end{array}\right]\]

同理

\[S_{2v}=\left[\begin{array}{c}-10\\0\\10\\0\end{array}\right]\]

所以

\[S_{uv}=\left[\begin{array}{cccc}10&0&-10&0\\0&0&0&0\\-10&0&10&0\\0&0&0&0\end{array}\right]\]

\((b)\)

根据\(a\)中你的结果，计算以下像素块\(B\)的2D-DCT。

\[B=\left[\begin{array}{cccc}20&20&20&20\\20&15&15&20\\20&15&15&20\\20&20&20&20\end{array}\right]\]

解：

由题可知，

\[B=\left[\begin{array}{cccc}20&20&20&20\\20&20&20&20\\20&20&20&20\\20&20&20&20\end{array}\right]-\frac12A\]

令

\[C=\left[\begin{array}{cccc}20&20&20&20\\20&20&20&20\\20&20&20&20\\20&20&20&20\end{array}\right]\]

由于DCT是线性变换，所以

\[S_B=S_C-\frac12S_A\]

又对于\(C\)有，

\[\begin{aligned}F_{C0v}&=\alpha(v)\sum_{j=0}^{3}s_{ij}\cos\frac{(2j+1)v\pi}{8}\\&=20\alpha(v)\left(\cos\frac{v\pi}8+\cos\frac{3v\pi}8+\cos\frac{5v\pi}8+\cos\frac{7v\pi}8\right)\end{aligned}\]

若\(v\)为奇数，

\[\begin{aligned}F_{C0v}&=20\alpha(v)\left(\cos\frac{v\pi}8+\cos\frac{3v\pi}8+\cos\left(-\frac{5v\pi}8\right)+\cos\left(-\frac{7v\pi}8\right)\right)\\&=20\alpha(v)\left(\cos\frac{v\pi}8+\cos\frac{3v\pi}8-\cos\left(v\pi-\frac{5v\pi}8\right)-\cos\left(v\pi-\frac{7v\pi}8\right)\right)\\&=20\alpha(v)\left(\cos\frac{v\pi}8+\cos\frac{3v\pi}8-\cos\frac{3v\pi}8-\cos\frac{v\pi}8\right)\\&=0\end{aligned}\]

则

\[F_{C00}=20\sqrt\frac14(1+1+1+1)=40\]

\[F_{C01}=0\]

\[F_{C02}=20\sqrt\frac12\left(\cos\frac\pi4+\cos\frac{3\pi}4+\cos\frac{5\pi}4+\cos\frac{7\pi}4\right)=0\]

\[F_{C03}=0\]

则

\[F_{Civ}=\left[\begin{array}{cccc}40&0&0&0\\40&0&0&0\\40&0&0&0\\40&0&0&0\end{array}\right]=2\left[\begin{array}{cccc}20&0&0&0\\20&0&0&0\\20&0&0&0\\20&0&0&0\end{array}\right]\]

因此

\[S_{C}=2\left[\begin{array}{cccc}40&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{array}\right]=\left[\begin{array}{cccc}80&0&0&0\\0&0&0&0\\0&0&0&0\\0&0&0&0\end{array}\right]\]

因此

\[\begin{aligned}S_B&=S_C-\frac12S_A\\&=\left[\begin{array}{cccc}75&0&5&0\\0&0&0&0\\5&0&-5&0\\0&0&0&0\end{array}\right]\end{aligned}\]

上述将一个2D DCT分解为两个1D DCT可以通过两个连续的矩阵乘法来实现

\[F(u,v)=T\cdot f(i,j)\cdot T^\intercal\]

我们将T命名为DCT矩阵

\[T[i,j]=\begin{cases}\sqrt\frac1N&,i=0\\\sqrt\frac2N\cos\frac{(2j+1)i\pi}{2N}&,i\gt0\end{cases}\]

当\(N=8\)时，有

\[T_8[i,j]=\begin{cases}\frac1{2\sqrt2}&,i=0\\\frac12\cos\frac{(2j+1)i\pi}{16}&,i\gt0\end{cases}\]

\[T_8=\left[\begin{array}{ccccc}\frac1{2\sqrt2}&\frac1{2\sqrt2}&\frac1{2\sqrt2}&\cdots&\frac1{2\sqrt2}\\\frac12\cos\frac\pi{16}&\frac12\cos\frac{3\pi}{16}&\frac12\cos\frac{5\pi}{16}&\cdots&\frac12\cos\frac{15\pi}{16}\\\frac12\cos\frac\pi8&\frac12\cos\frac{3\pi}8&\frac12\cos\frac{5\pi}8&\cdots&\frac12\cos\frac{15\pi}8\\\frac12\cos\frac{3\pi}{16}&\frac12\cos\frac{9\pi}{16}&\frac12\cos\frac{15\pi}{16}&\cdots&\frac12\cos\frac{45\pi}{16}\\\vdots&\vdots&\vdots&\ddots&\cdots\\\frac12\cos\frac{7\pi}{16}&\frac12\cos\frac{21\pi}{16}&\frac12\cos\frac{35\pi}{16}&\cdots&\frac12\cos\frac{105\pi}{16}\end{array}\right]\]

2D IDCT（逆离散余弦变换）矩阵实现如下

\[f(i,j)=T^\intercal\cdot F(u,v)\cdot T\]

DCT矩阵是正交的，因此，

\[T^\intercal=T^{-1}\]

练习：使用矩阵实现的2D-DCT

\(N\times N\)像素块的二维离散余弦变换（2D DCT）矩阵由下式给出

\[T[i,j]=\begin{cases}\sqrt\frac1N&,i=0\\\sqrt\frac2N\cos\frac{(2j+1)i\pi}{2N}&,i\gt0\end{cases}\]

其中\(i\)和\(j\)分别是行和列索引

\((ⅰ)\)

确定\(4\times4\)像素块的2D DCT矩阵\(T\)。将答案四舍五入到小数点后\(4\)位。

~~mmd我没带计算器，因此直接使用编程打表~~

#include <cmath>
#include <cstdio>

int n;

double mat[20][20];

int main(int argc, char **argv) {
  scanf("%d", &n);

  for (int j = 0; j < n; ++j) mat[0][j] = 1.0 / sqrt((double)n);

  for (int i = 1; i < n; ++i) {
    for (int j = 0; j < n; ++j) {
      mat[i][j] =
          sqrt(2.0 / (double)n) *
          cos(((2.0 * (double)j + 1.0) * (double)i * M_PI) / (2.0 * (double)n));
    }
  }

  for (int i = 0; i < n; ++i) {
    for (int j = 0; j < n; ++j) {
      printf("%.4lf ", mat[i][j]);
    }
    putchar('\n');
  }

  return 0;
}

由程序可得

\[T_4=\left[\begin{array}{cccc}0.5000&0.5000&0.5000&0.5000\\0.6533&0.2706&-0.2706&-0.6533\\0.5000&-0.5000&-0.5000&0.5000\\0.2706&-0.6533&0.6533&-0.2706\end{array}\right]\]

\((ⅱ)\)

根据在部分\((ⅰ)\)中的结果，计算以下像素块\(A\)的2D DCT。将答案四舍五入到小数点后\(3\)位。

\[A=\left[\begin{array}{cccc}20&20&0&0\\20&20&0&0\\0&0&0&0\\0&0&0&0\end{array}\right]\]

还是编程大法（）

import numpy as np

T = np.asmatrix([[0.5000, 0.5000, 0.5000, 0.5000],
                 [0.6533, 0.2706, -0.2706, -0.6533],
                 [0.5000, -0.5000, -0.5000, 0.5000],
                 [0.2706, -0.6533, 0.6533, -0.2706]])

A = np.asmatrix([[20.0, 20.0, 0.0, 0.0],
                [20.0, 20.0, 0.0, 0.0],
                [0.0, 0.0, 0.0, 0.0],
                [0.0, 0.0, 0.0, 0.0]])

print(np.round(np.dot(np.dot(T, A), T.T), 3))

~~懒到不想写矩阵乘法~~

由程序可得

\[TAT^\intercal=\left[\begin{array}{cccc}20.000&18.478&0.000&-7.654\\18.478&17.072&0.000&-7.072\\0.000& 0.000&0.000&0.000\\-7.654&-7.072&0.000&2.929\end{array}\right]\]

JPEG标准

图像内容在整个图像中变化相对较慢，例如在\(8\times8\)图像块内
人类对高空间频率分量的失真比低频分量的失真更不敏感
人类对强度（亮度）成分比颜色（色度）成分更敏感

JPEG 是一种流行的图像压缩标准，能够解决有损和无损图像压缩问题，压缩率范围从10:1到20:1。

四种操作模式：

基于顺序DCT的模式
基于渐进DCT的模式
无损模式
分层模式

我们将重点关注基于顺序DCT的模式，即基线JPEG，因为它是JPEG中最流行的模式

基线JPEG中的主要阶段

图像/块处理
对图像块进行DCT
量化
熵编码
框架构建

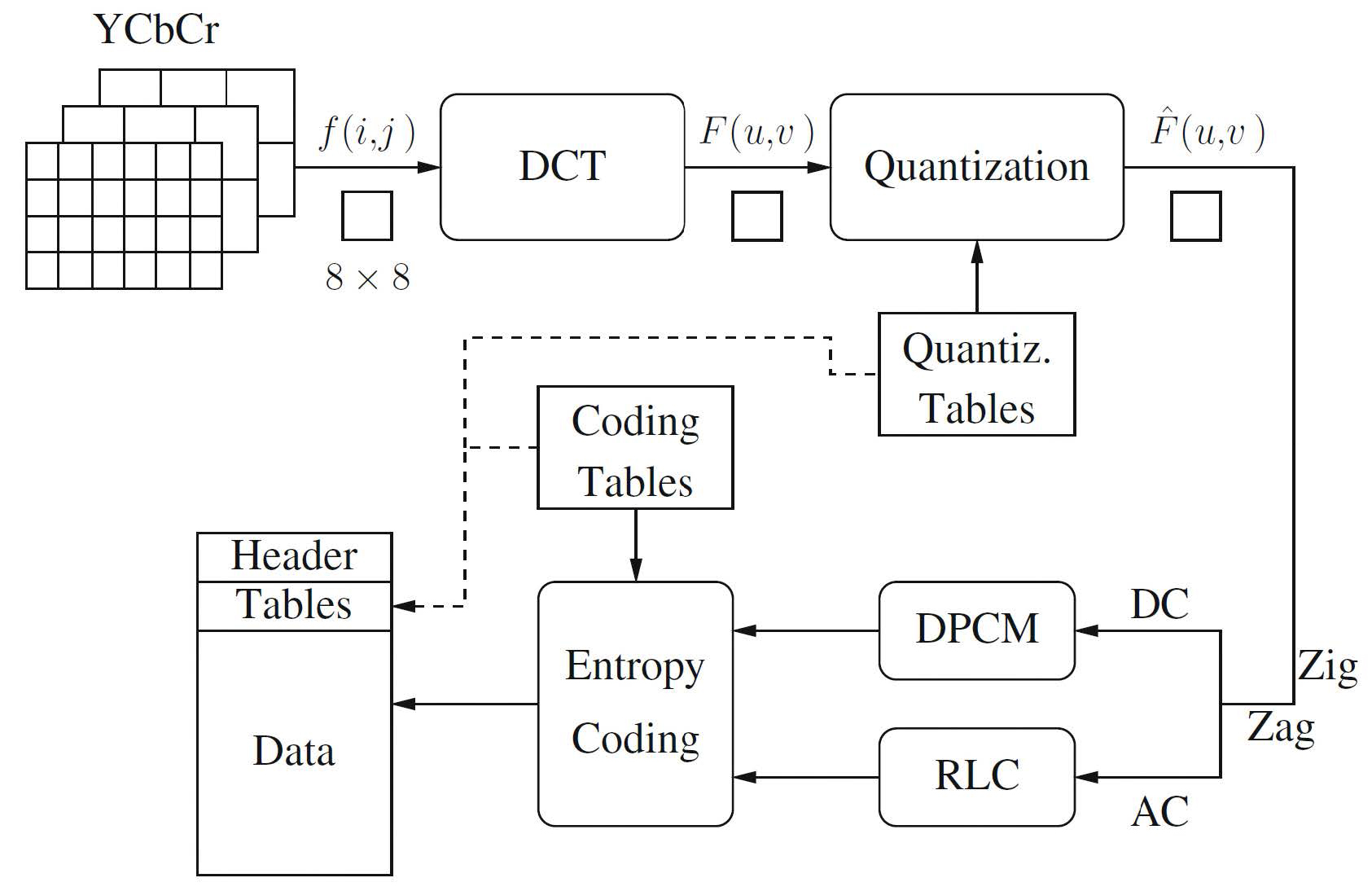
图像分区

首先将图像分割成多个\(8\times8\)像素块

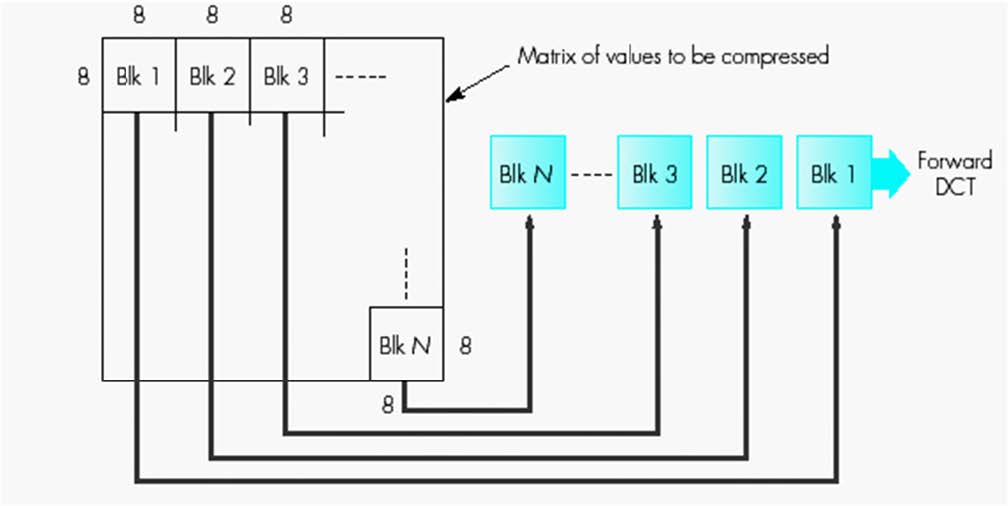
前向DCT

对每个\(8\times8\)像素块应用前向2D DCT。

将图像数据转换为更适合压缩的形式
2D DCT产生能量压缩
2D DCT通过降低变换系数之间的相关性来减少冗余

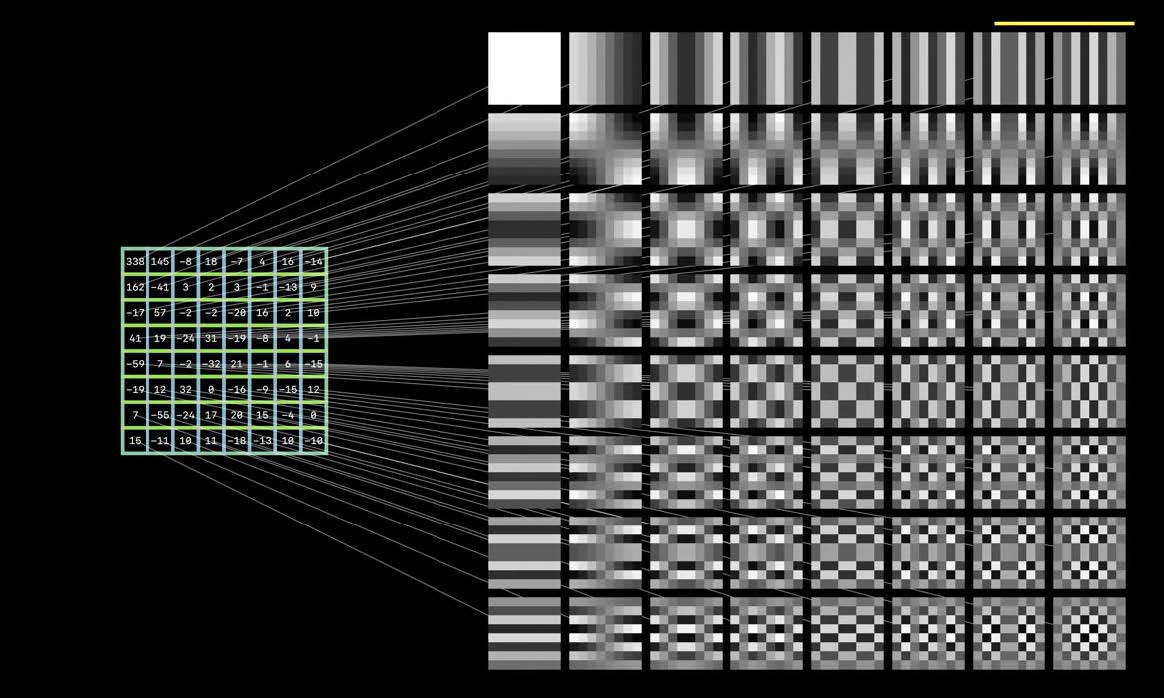
JPEG DCT基函数

DCT中基函数的变换

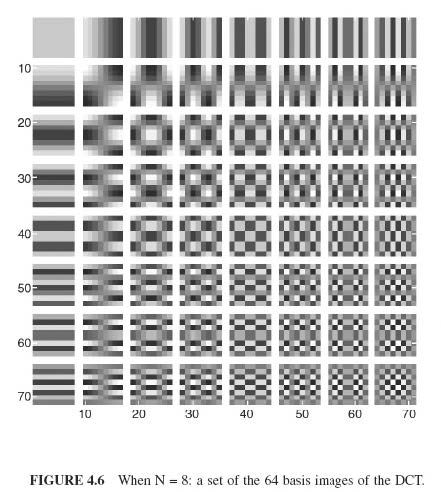
当N=8时：一组64个DCT基础图像 — 当\(N=8\)时：一组\(64\)个DCT基础图像

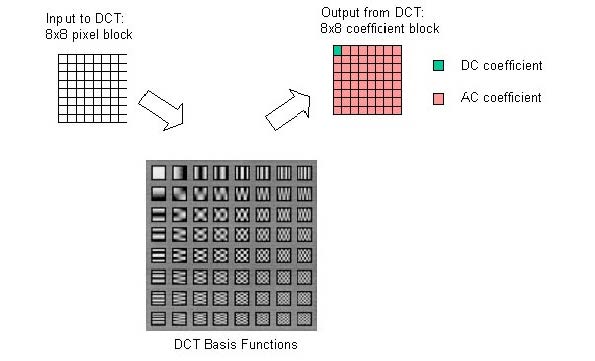
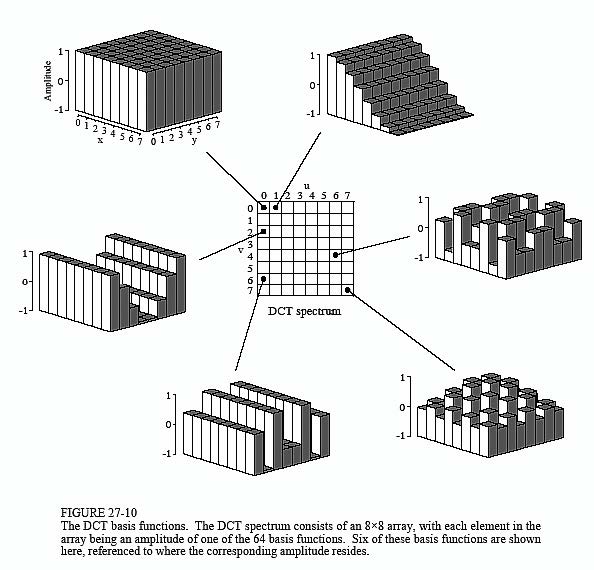
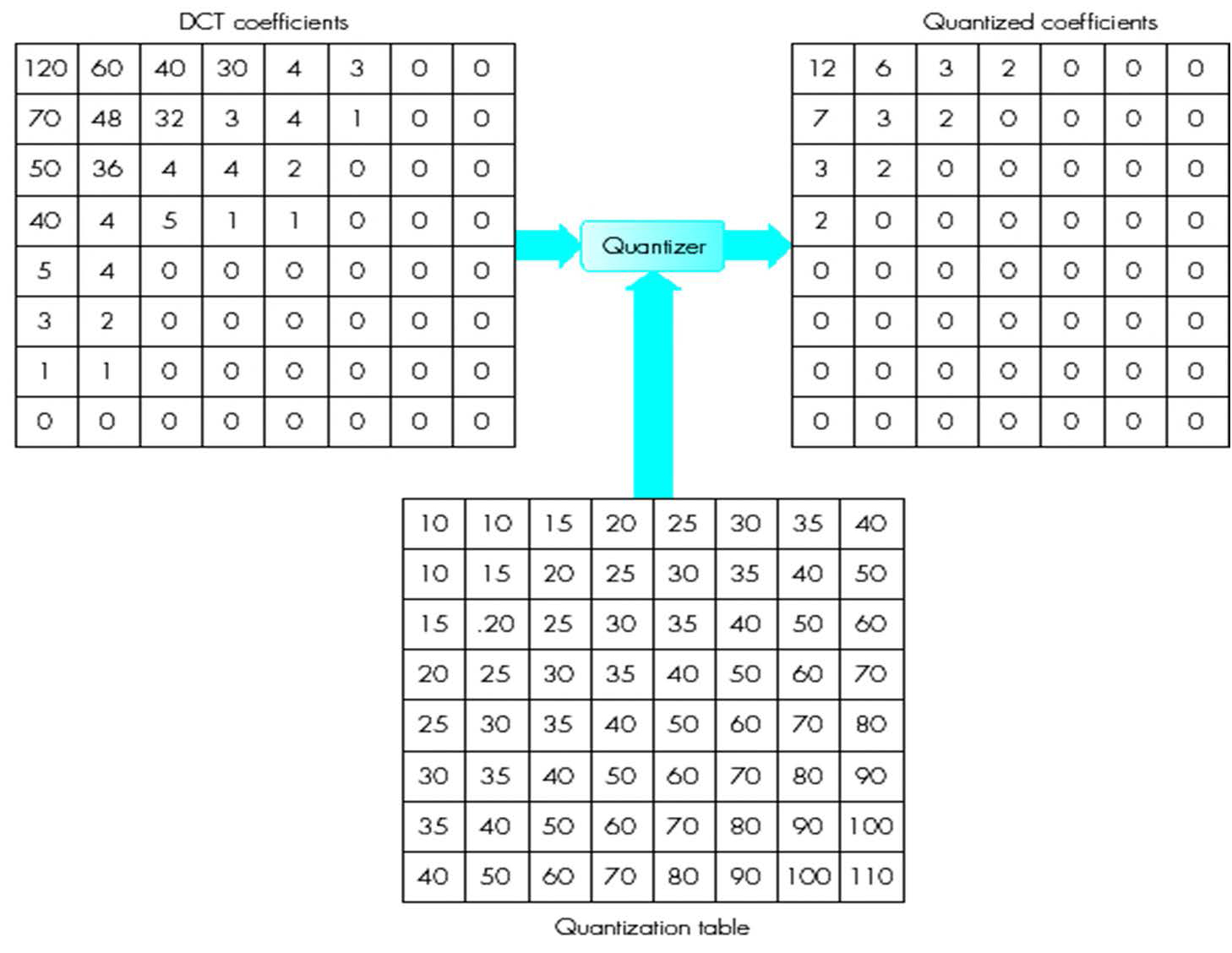
量化

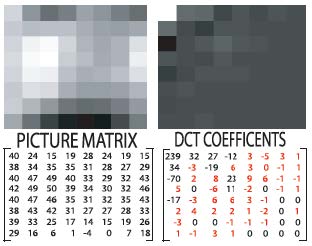
由于使用有限数量的位数来表示DCT系数，因此需要量化将连续值映射为离散值。使用量化表对系数进行量化，量化过程中会发生信息损失。

人类对DC和低频AC系数更敏感
因此，应更加重视量化它们
使用较小的步长（量化值）来量化DC和低频AC系数，以减少量化误差
量化表中的步长/值是压缩级别和信息损失之间的折衷

\(F(u,v)\)表示DCT系数，\(Q(u,v)\)是“量化矩阵”条目，\(\hat F(u,v)\)表示JPEG在后续熵编码中将使用的量化DCT系数

\[\hat F(u,v)=\text{round}\left[\frac{F(u,v)}{Q(u,v)}\right]\]

后面一堆影响啥的，具体就去看前面那个视频吧。

练习：基函数与量化

在一个新的图像压缩方案中，一名学生希望按照基线JPEG中的类似步骤进行灰度图像压缩。然而，该学生建议将图像分割成多个\(4\times4\)像素块，对每个像素块执行\(4\times4\) DCT，然后进行相应的量化和熵编码。

\((ⅰ)\)

简要讨论此新压缩方案中使用的DCT基函数与基线JPEG压缩中使用的基函数之间的主要相似点和主要不同点。

相似点：流程相同，仍然是分块-DCT-量化-熵编码
不同点：只有亮度通道，不需要对CbCr通道压缩；分割大小不同，所需的DCT矩阵和量化矩阵不同

\((ⅱ)\)

为这种新的压缩方案写出合适的量化表。简要说明你的答案。

~~Thanks to ChatGPT~~

\[\left[\begin{array}{cccc}16&11&10&16\\12&12&14&19\\14&13&16&24\\14&17&22&29\end{array}\right]\]

左上角（低频区域）：这些值较小，表示较细致的量化，以保留图像的主要结构信息。
右下角（高频区域）：这些值较大，表示较粗糙的量化，用于减少细节信息，这样可以在不显著影响视觉质量的情况下有效压缩图像。

在基线JPEG的\(8\times8\)量化表中，数值差距较大，因为较大块的DCT块（\(8\times8\)）包含更多的高频分量，而这些高频分量对图像质量的影响较小，所以可以较大幅度地量化。在\(4\times4\) DCT中，由于每个块的频率范围较小，高频分量的数量较少，因此量化表中的数值可能不会像\(8\times8\) DCT中的数值差距那么显著。

熵编码

熵编码包括4个步骤：

矢量化（之字形扫描）
差分编码/差分脉冲编码调制（DPCM）
行程编码（RLE）
Huffman编码

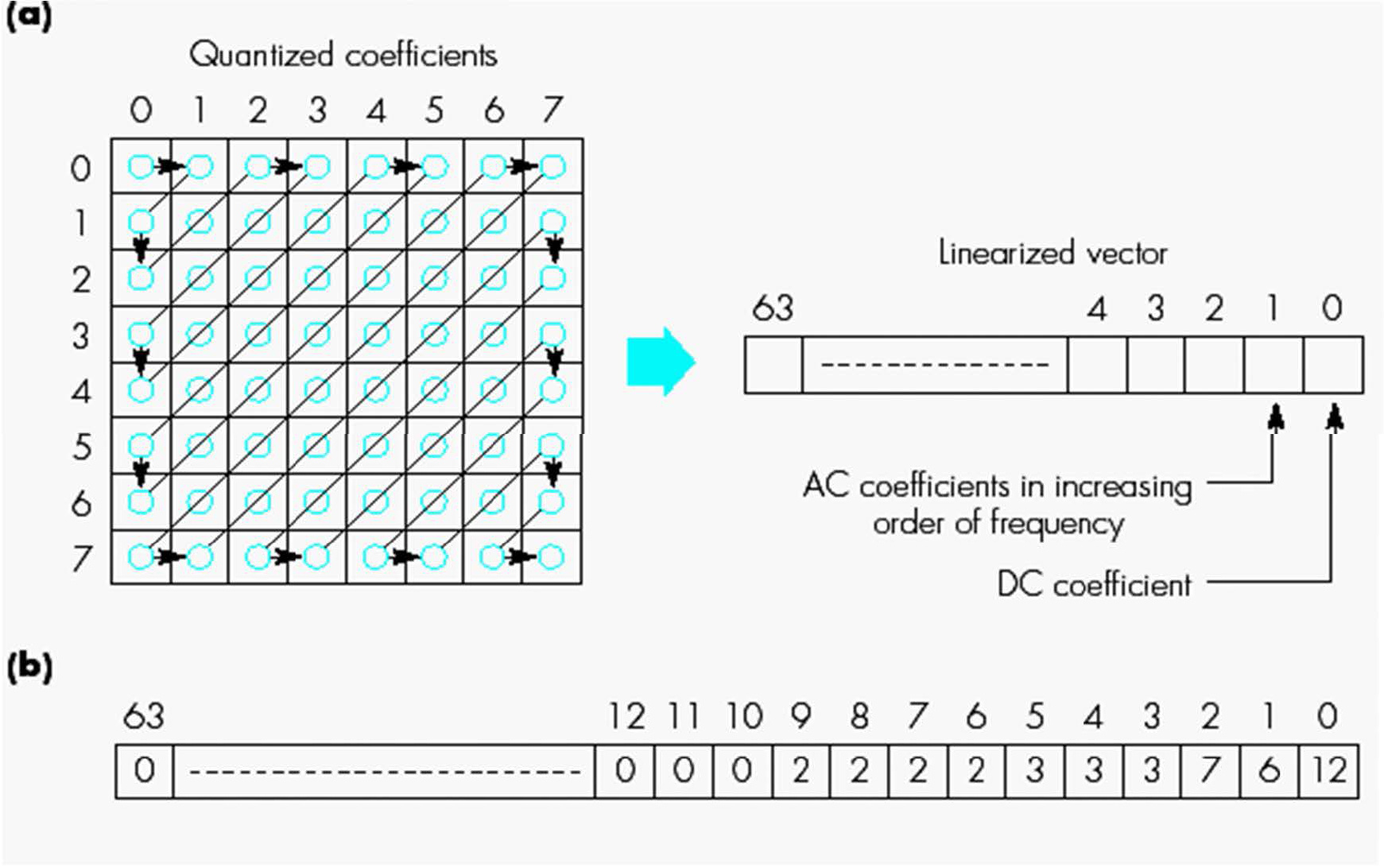
矢量化

通过之字形扫描，用一维向量表示量化的二维矩阵，目的在于利用量化矩阵中大量零的存在。

DC系数的差分编码

DC系数与63个AC系数分开处理，反映像素块的平均强度
DC系数采用差分编码进行编码，对当前块和前一个块的DC系数之间的差异（预测误差）进行编码。由于两个连续块之间的平均强度相似，因此使用差分编码。

行程编码（RLE）

AC系数采用行程编码进行编码
行程编码尝试将零组合在一起，从而利用AC值中存在大量零的情况
行程编码语法使用由成对的值组成的字符串
每对都有(skip, value)格式：
- skip – 这一程的零数
- value – 下一个非零系数

Huffman编码

经过差分编码和行程编码后，一些符号/模式比其他符号/模式出现的频率更高。因此，使用Huffman编码来压缩这些符号。通过用较短的代码字替换频繁模式，可以实现高压缩，反之亦然。哈夫曼编码用于差分编码和行程编码。

帧构建

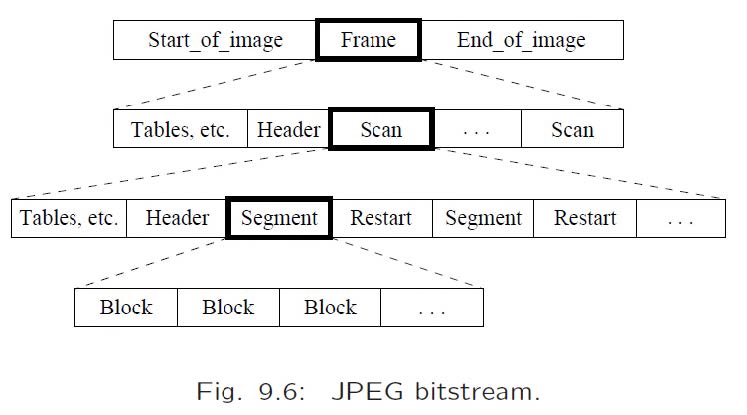
JPEG定义与图像/帧相关的比特流语法。帧构建器的作用是将与编码图像相关的所有信息封装在此格式中。

JPEG比特流格式

JPEG解码器

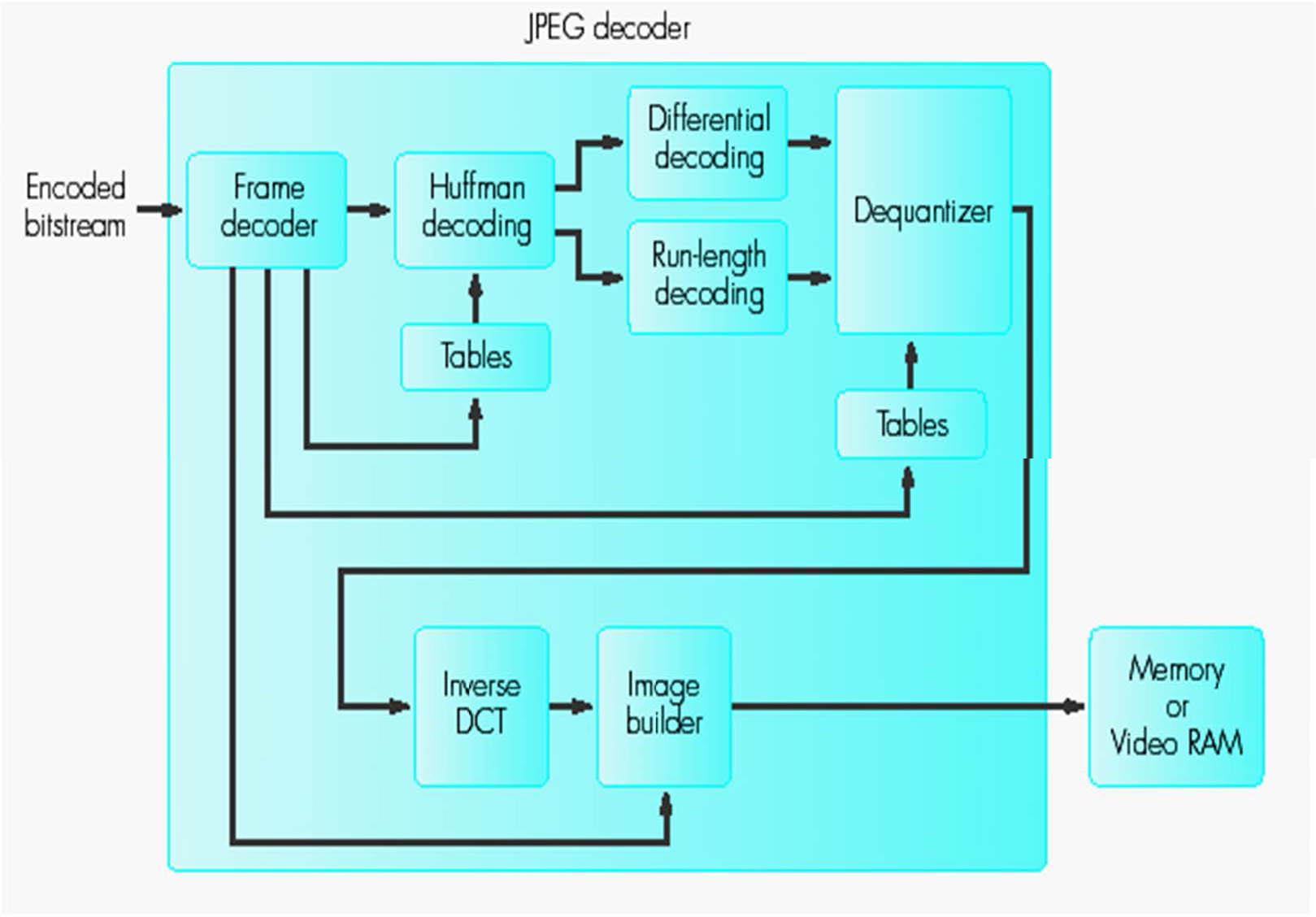
JPEG解码器提取控制信息和表，然后将它们传递给图像生成器。

采用霍夫曼解码获得DC和AC符号
采用差分解码获得DC系数
采用行程解码获得AC系数
将DC和AC系数放在一起，并使用量化表进行反量化
逆DCT用于将DCT系数变换为像素块
图像生成器从所有像素块重建图像