启发式搜索与博弈
启发式搜索概念
无知搜索策略仅使用问题定义中可用的信息。
- 系统地生成新状态
- 效率低下
- 流行方法:广度优先搜索、深度优先搜索、迭代深化搜索
有知搜索策略使用针对具体问题的知识来指导搜索。
- 使用评估函数来估计每个节点的“可取性”
- 通常更有效
- 流行方法:爬山法、最佳优先搜索(贪心)、A*
启发式(adj.)一词的字面意思是:
- 基于个人发现和经验的学习
- 在发现过程中帮助他人(盟友/对手)
启发式(n.)一词的字面意思是
- (研究)利用经验和实际努力来寻找问题的答案或提高绩效
在状态空间搜索中,启发式方法形式化为:
- 在状态空间中选择最有可能导致可接受问题解决方案的分支的规则
为何采用启发式方法?
我们被迫使用启发式方法,因为寻找解决方案的计算成本通常过高
- 在许多问题中,状态空间的增长是组合爆炸式增长,可能状态的数量随着搜索深度呈指数或阶乘增长
- 在这些情况下,穷举式强力搜索技术可能无法在任何实际时间内找到解决方案
- 启发式方法通过引导搜索沿着空间中最“有希望”的路径进行,从而解决上述复杂性
- 通过消除状态及其后代,启发式算法有望击败状态空间图的组合爆炸并找到可接受的答案
- 例如,国际象棋、围棋、“大型”TSP(n > 25)
启发式算法的局限性
与许多发现和发明规则一样,启发式方法也存在缺陷
- 启发式方法只是一种有根据的猜测。由于启发式方法使用的信息有限,例如当前正在评估的状态的描述,因此它们很少能够预测搜索过程中状态空间的确切行为
- 启发式方法可能导致搜索算法得到次优解决方案或根本找不到任何解决方案。启发式搜索的这种固有局限性无法通过“更好”的启发式方法或更高效的搜索算法来消除
启发式搜索的两个关键组成部分
- 启发式测量
- 使用启发式测量搜索状态空间的算法
获取启发式函数\(h\)的示例
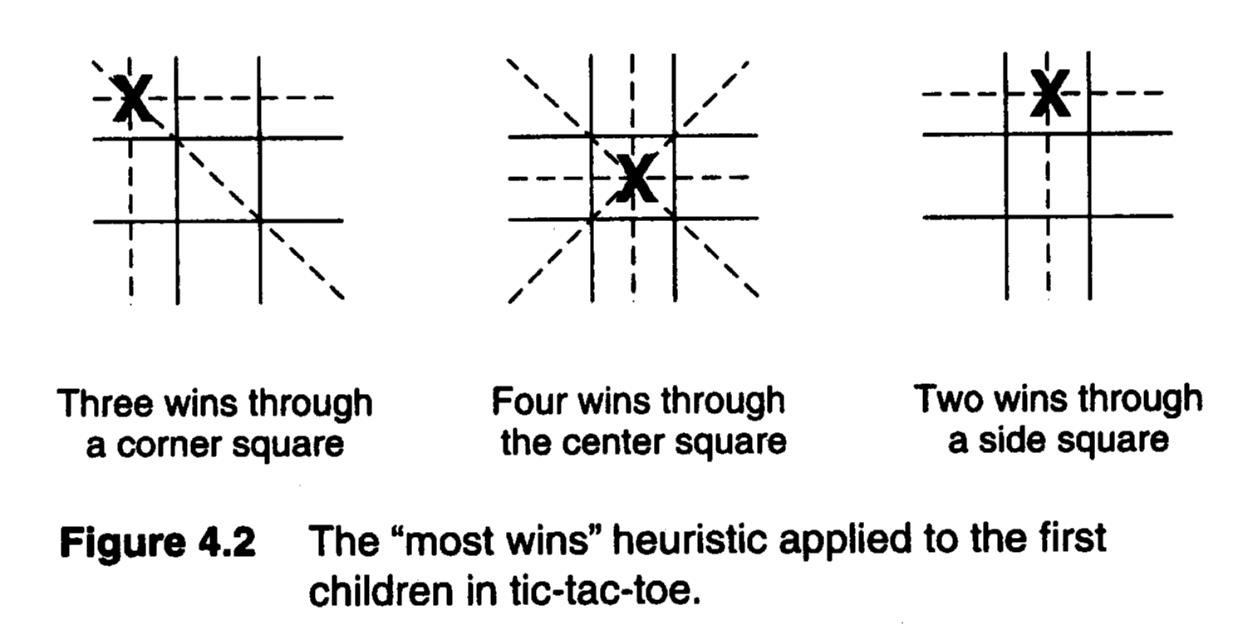
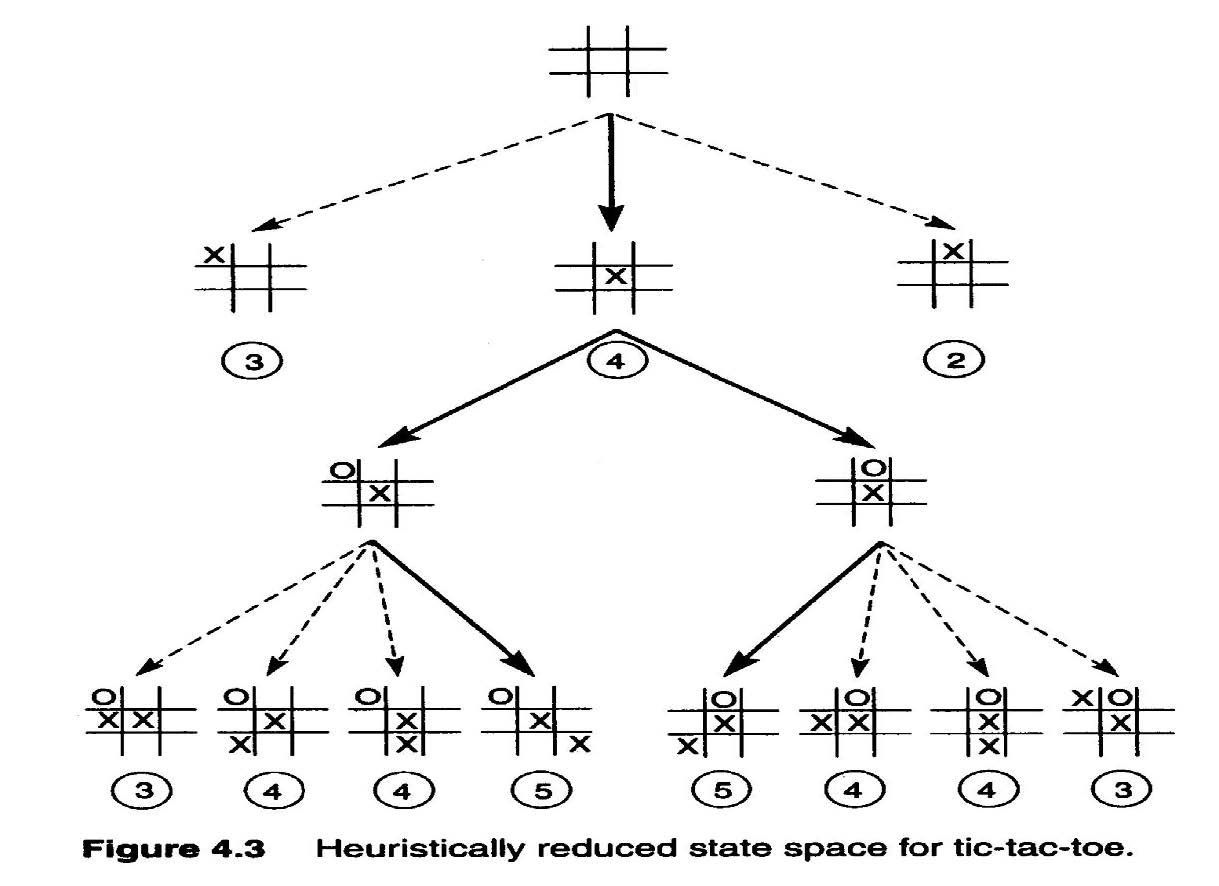
启发式搜索算法
爬山法
爬山法:以一位热切但目光短浅的登山者命名
- 爬山法策略会扩展搜索中的当前节点并评估其子节点
- 选择最佳子节点进行进一步扩展;不会保留其兄弟节点和父节点
- 当搜索达到比其任何子节点都更好的状态时,搜索将停止
爬山策略的局限性
错误的启发式算法可能导致无限失败
爬山策略也可能陷入局部最大值
如果局部最大值不是目标,算法将无法找到解决方案
通常,启发式搜索需要更明智的算法;最佳优先搜索可提供这种算法
如果启发式 = 适应度或优度,则越大越好:“爬山法”、“局部最大值”。
如果启发式 = 成本,则越小越好:“梯度下降”、“局部最小值”。例如,TSP 中的行程长度
最佳优先搜索(Best-First Search)
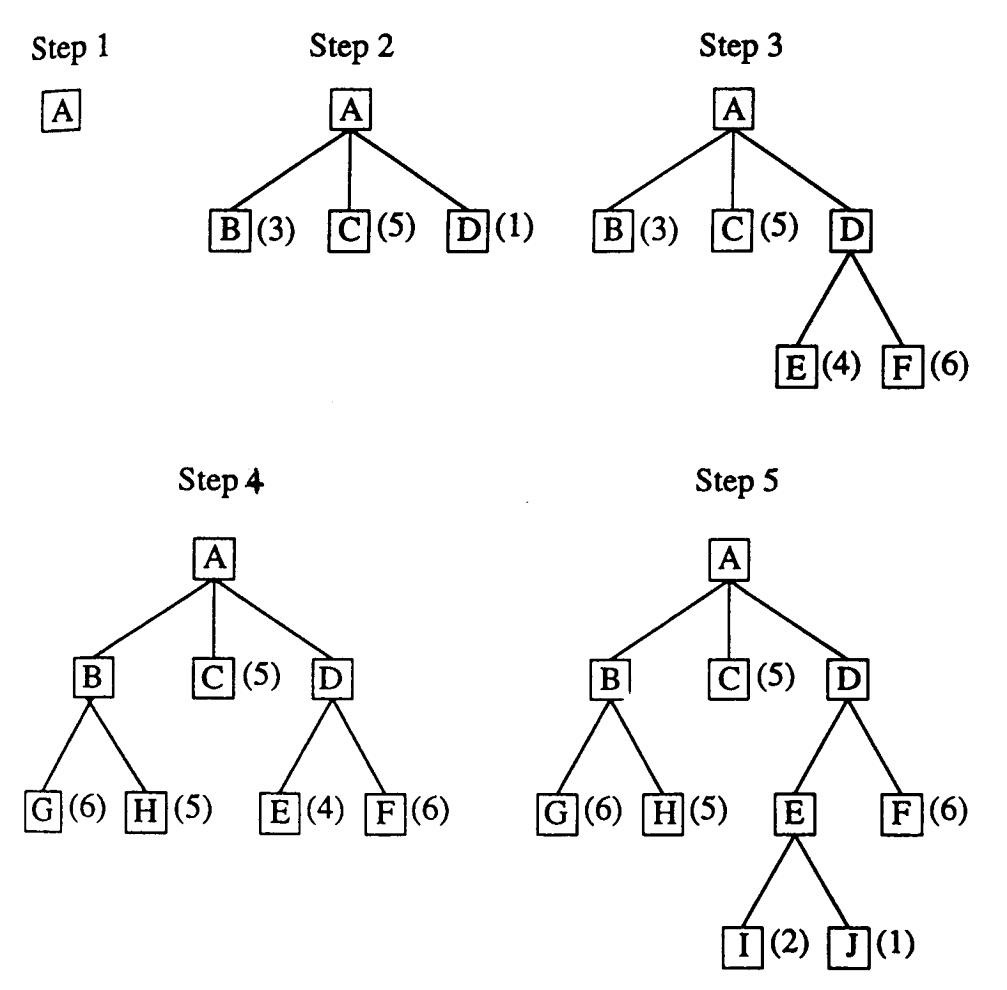
- 从仅包含初始状态的OPEN开始
- 直到找到目标或OPEN上没有剩余节点,执行以下操作:
- 选择OPEN上的最佳节点
- 生成其后继节点
- 对于每个后继节点,执行以下操作:
- 如果之前未生成,则对其进行评估,将其添加到OPEN,并记录其父节点
- 如果之前已生成,则如果此新路径比前一个路径更好,则更改父节点。更新从起始状态到达此节点的成本
制定启发式方法
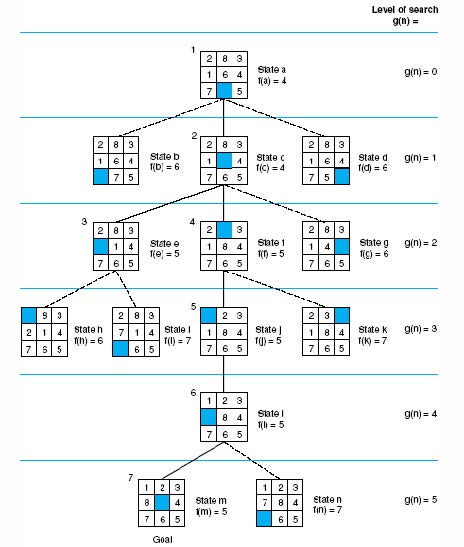
可以将深度计数添加到每个状态的启发式评估中,以便偏向于图中较浅的状态进行搜索。这使得评估函数(成本)\(f\)成为两个部分的总和
\[f(n)=g(n)+h(n)\]
- \(g(n)\):路径成本函数 = 从初始状态到当前状态\(n\)的cost。或者,它测量从起始状态(深度计数)到任何状态\(n\)的路径的实际长度(没有关于到达目标的成本的信息)。
- \(h(n)\):启发式函数 = 从\(n\)到目标状态的最便宜路径的估计成本。\(h(n)\)不大于实际成本(可接受)
最佳优先
- \(g(n)\):路径成本函数 = 从起始状态到状态\(n\)的成本
- \(h(n)\):启发式函数 = 从\(n\)到目标状态的估计成本
评估函数\(f(n)\)可能包含各种因素,如预期剩余路径成本、成功概率等……
贪心最佳优先
- \(g(n)\):路径成本函数 = 0
- \(h(n)\):启发式函数 = 从\(n\)到目标状态的估计成本
贪心最佳优先,使用启发式方法优先考虑更接近目标(速度)的节点
A*算法
A*搜索结合了广度优先搜索和贪心最佳优先的优势。与BFS类似,它可以找到最短路径,并且与贪婪最佳优先类似,它速度很快。
每次迭代,A*都会选择边界上的节点,以最小化:
- \(g(n)\) - 从源开始的步数:与BFS类似,首先查看靠近源的节点(彻底性)
- \(h(n)\) - 近似步数到目标:与贪心最佳优先类似,使用启发式方法优先考虑更接近目标(速度)的节点
\[f(n) = g(n) + h(n)\]
- \(g(n)\)测量从任意状态\(n\)到起始状态的路径的实际长度(深度计数)
- \(h(n)\)是状态\(n\)的可接受启发式估计(成本),即\(h(n)\leq h^*(n)\),其中\(h^*(n)\)为状态\(n\)的真实成本,例如\(h_\text{SLD}(n)\)永远不会超过真实距离(SLD为Straight-line distance)
博弈
搜索 – 没有对手
- 解决方案是寻找目标的(启发式)方法
- 启发式和CSP技术可以找到最佳解决方案
- 评估函数:通过给定节点从起点到目标的成本估算
- 示例:路径规划、调度活动……
博弈 – 对手 + 时间
- 解决方案是策略,策略指定每个可能的对手回应的移动。
- 时间限制强制近似解决方案。
- 评估函数:评估游戏位置的“优劣”
- 示例:国际象棋、跳棋、围棋……
策略 - Minimax:
- 尝试最小化对手在每个状态下的最大奖励
- 穷举搜索
缺点
- 需要分析的动作数量会迅速增加。
- 计算能力限制了算法的深度。
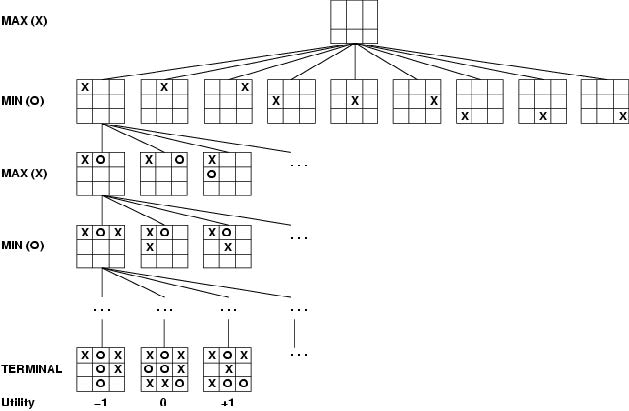
- 结束状态的效用值是从MAX的角度来看的。
- MAX使用搜索树来确定最佳移动
博弈作为搜索问题
- 初始状态:初始棋盘配置和指示谁先动
- 操作符:合法动作
- 终端测试:确定游戏何时结束。游戏结束的位置:终端状态
- 效用函数(收益函数):返回数字分数以量化游戏结果
Minimax:博弈中的启发式方法
极小最大搜索策略:找到导致最终状态(目标)的一系列动作,最大化自己的效用并最小化对手的效用 - 假设对手也这样做
详尽可搜索图上的Minimax程序 - 博弈树
- 双人游戏比简单的谜题更复杂,因为存在一个无法预测其动作的对手
- 在玩状态空间可能被详尽描述的游戏时,主要困难在于解释对手的行为
- 最简单的解决方案是假设对手使用相同的状态空间知识,并运用这些知识不断努力赢得游戏
- Minimax在此假设下实现游戏搜索
- 游戏中的对手被称为MIN和MAX
示例:NIM游戏
玩NIM时,两位对手之间的桌子上会放有若干根火柴;每走一步,玩家必须将一堆火柴分成两堆非空的火柴,每堆火柴的数量不同。第一个无法继续走一步的玩家将输掉游戏。
对于合理数量的火柴,可以彻底搜索状态空间。
减法游戏:将一堆火柴分成两个非空且不同的堆
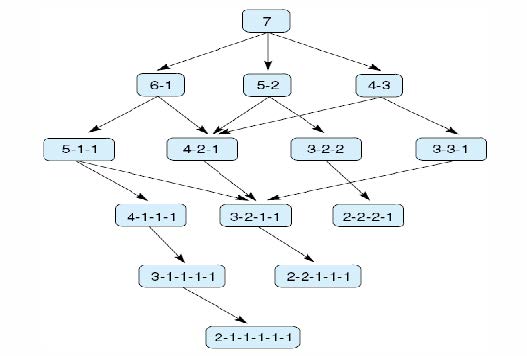
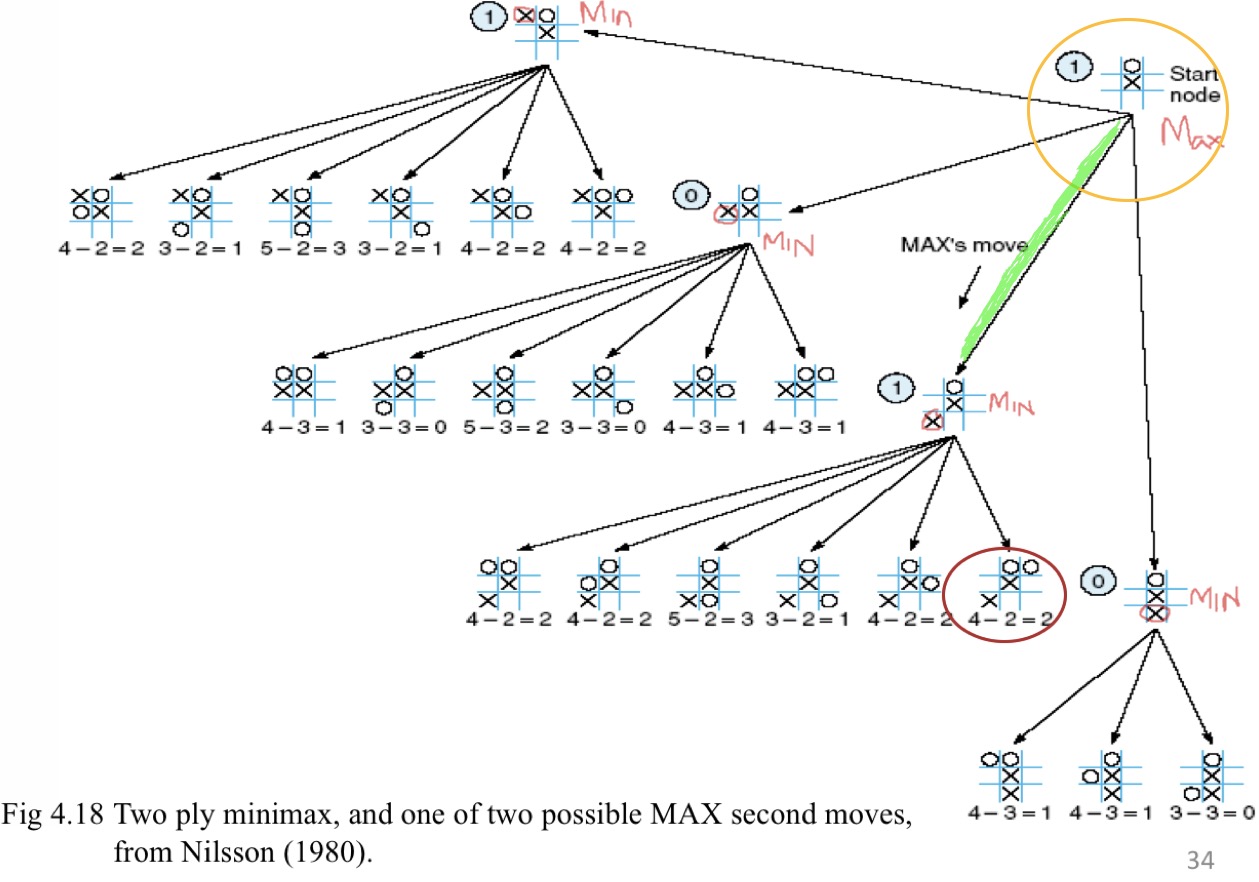
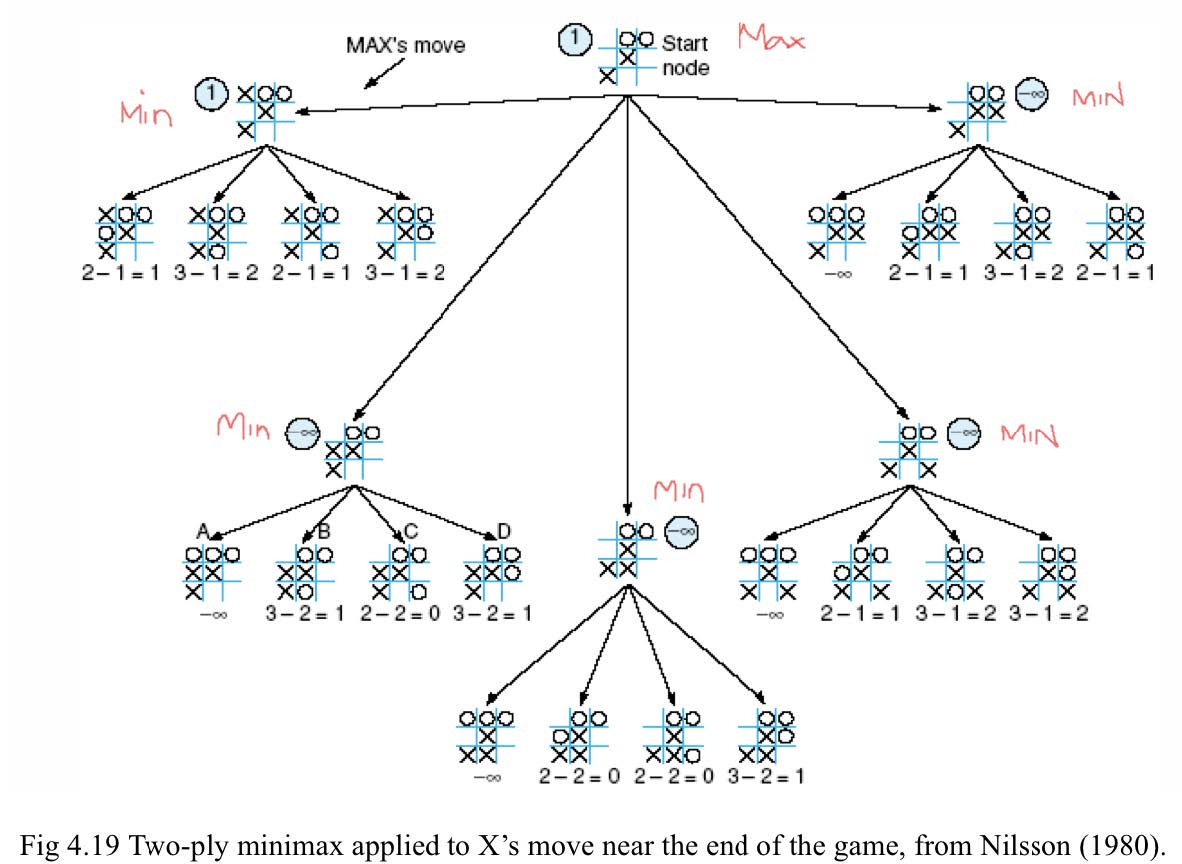
Minimax算法
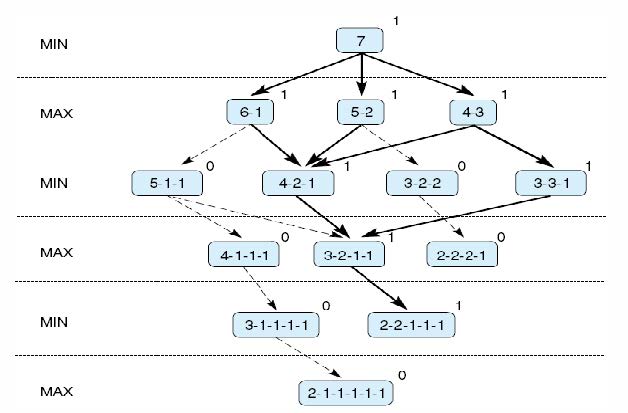
在实现Minimax时,我们根据游戏中此时谁的移动来标记搜索空间中的每个级别,MIN或MAX
每个叶节点被赋予一个值1或0,具体取决于它是MAX获胜还是MIN获胜。MINIMAX根据以下规则通过连续的父节点将这些值沿图向上传播:
- 如果父节点是MAX节点,则将其子节点中的最大值赋予它
- 如果父节点是MIN节点,则将其子节点中的最小值赋予它
这样分配给每个状态的值表示该玩家希望达到的最佳状态的值。这些派生值用于在可能的移动中进行选择。
完美决策 – 如果没有时间限制,则分为3步:
- 生成整个游戏树直至终端状态
- 计算效用
- 评估每个终端状态的效用
- 确定终端状态父级的最佳效用
- 对其父级重复该过程,直到到达根
- 选择最佳动作(即效用值最高的动作)
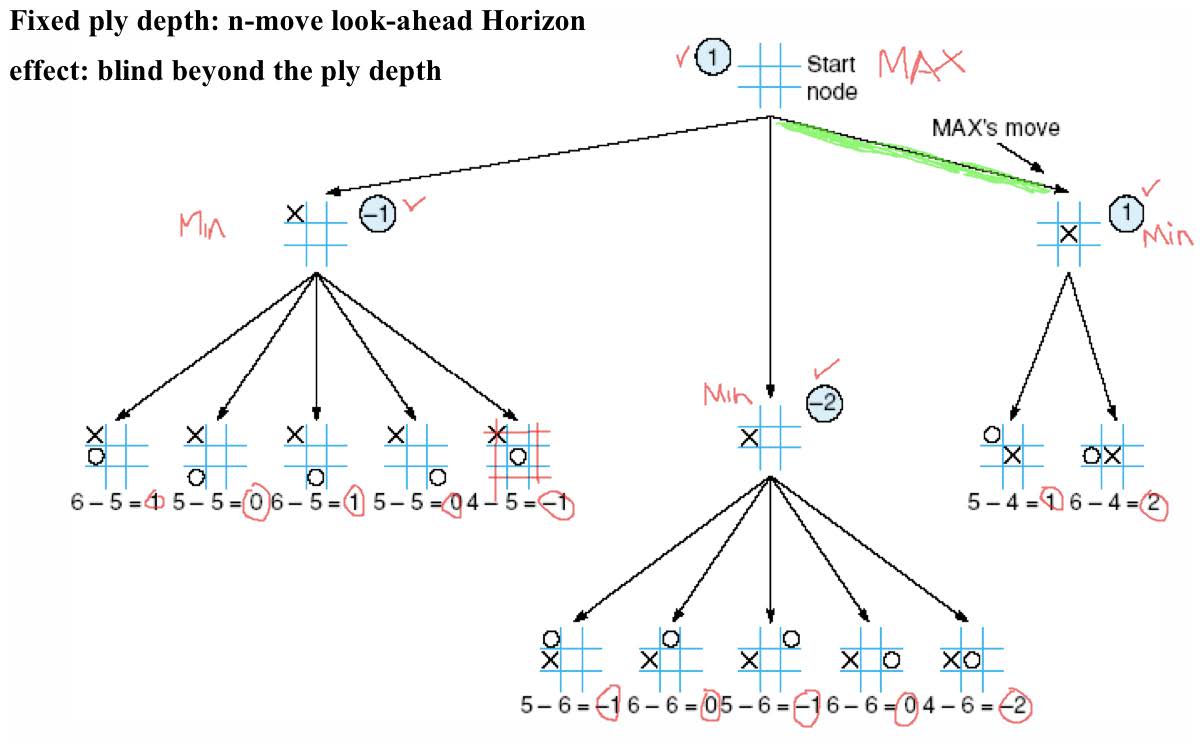
不完美决策 – 如果时间/空间限制:
- 用位置的估计可取性替换效用函数
- 评估函数
- 部分树搜索
- 例如,深度限制
- 用截止测试替换终端测试

Minimax的性质
- 完成? 是的,如果树是有限的(国际象棋有特定规则)
- 最佳? 是的,对抗最佳对手
- 时间复杂度? O(bm)
- 空间复杂度? O(b*m)(深度优先探索)
国际象棋:对于“合理”游戏,b=35,m=100,精确解完全不可行
但我们需要探索每条路径吗?搜索效率至关重要
Alpha-Beta算法
ALPHA-BETA算法 - 通过评估更少的节点得出与MINIMAX算法相同的结论。
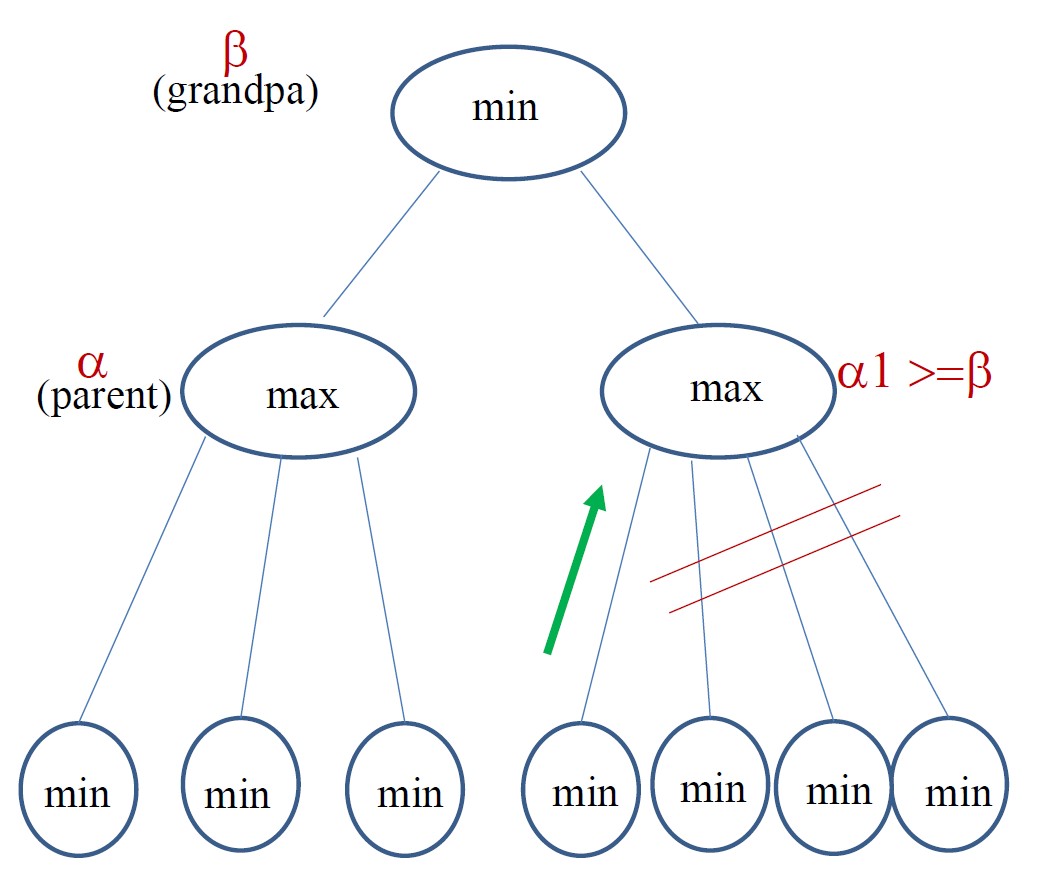
BEAT剪枝:
- 以深度优先的方式下降到完整的层深度,并将我们的启发式评估应用于一个状态及其所有兄弟节点。假设这些是MIN节点
- 然后将这些MIN值的最大值备份到父节点(MAX节点),并作为潜在的beta剪枝值提供给祖节点
- 下降到其他孙节点,如果其中任何值等于或大于此beta值,则终止对其父节点的探索。
规则:当任何MAX节点的alpha值大于或等于其任何MIN节点祖先的beta值时,搜索即可停止
ALPHA剪枝
- 以深度优先的方式下降到完整的层深度,并将我们的启发式评估应用于一个状态及其所有兄弟节点。假设这些是MAX节点
- 然后将这些MAX值的最小值备份到父节点(MIN节点),并作为潜在的alpha剪枝值提供给祖节点
- 下降到其他孙节点,如果其中任何值等于或小于此alpha值,则终止对其父节点的探索。
规则:当任何MIN节点的beta值小于或等于其任何MAX祖先的alpha值时,搜索即可停止
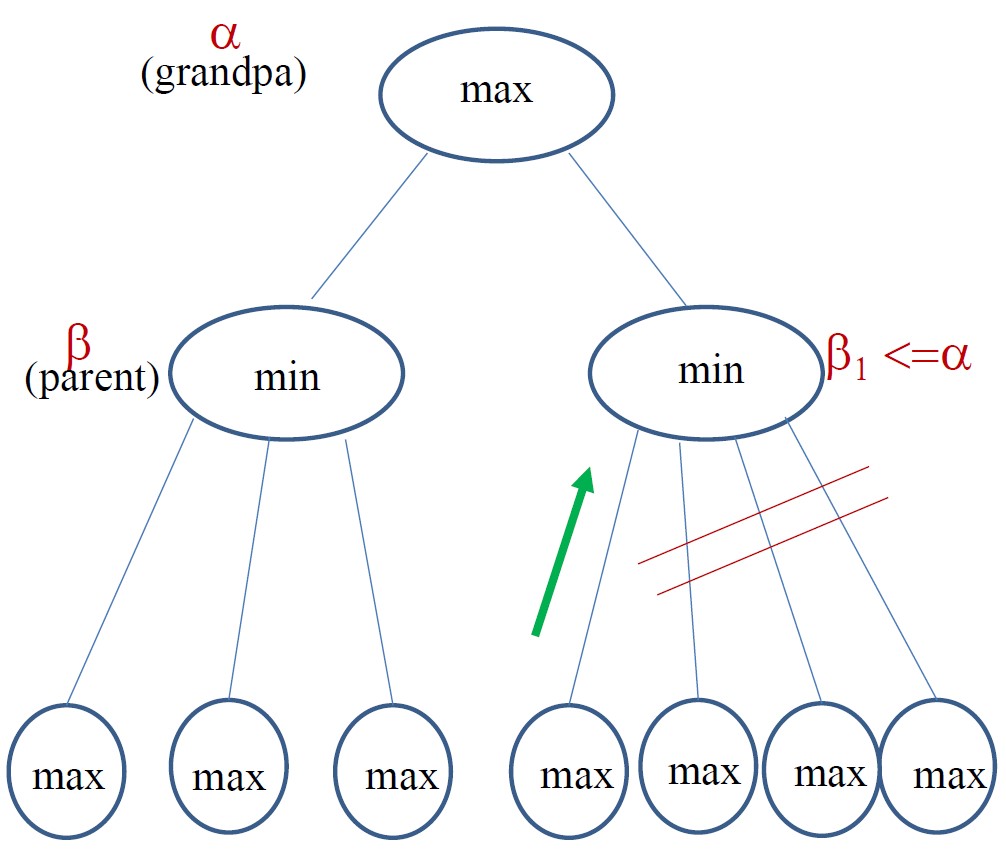
基于alpha和beta值的两条终止搜索规则为: - 如果MIN节点的beta值小于或等于其MAX祖先的alpha值,则搜索可停止 - 如果MAX节点的alpha值大于或等于其MIN节点祖先的beta值,则搜索可停止
Alpha-beta剪枝表达了第n层节点与第n+2层节点之间的关系
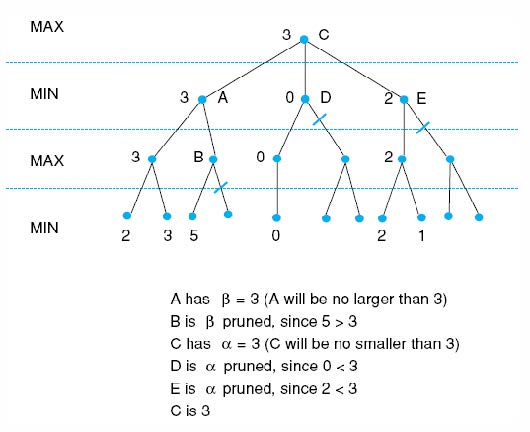
(解释:A是MIN,需要取左边3和右边B里面最小的;B是MAX,需要取子节点最大的,如果A的beta是3,那么B的子节点出现任意一个大于3的都会使B的alpha值大于3,那么A取最小的就必不可能取B,所以剪枝。)
Alpha-Beta的性质
- 修剪不会影响最终结果
- 良好的移动顺序可提高修剪的有效性
- 通过“完美排序”,时间复杂度=\(O(b^{m/2})\ \Rightarrow\) 可解深度加倍
- 关于哪些计算相关的推理价值的简单示例(一种元推理)
当暴力Minimax/Alpha-Beta不再适用时,围棋中存在如此多的潜在走法和反走法,它如何可能提前“计划”?
Monte Carlo树搜索
蒙特卡洛树搜索(MCTS)是一种用于某些决策过程的启发式搜索算法,最显著的是用于人工智能游戏的决策过程。
2006年,法国计算机科学家描述了蒙特卡罗方法在博弈树搜索中的应用,并为其命名。
它已用于棋盘游戏围棋、国际象棋和将棋等其他棋盘游戏以及桥牌、拼字游戏、Poke 等信息不完整的游戏……
许多其他应用:现实世界规划;优化……
核心思想:MCTS构建一个统计树,该统计树部分映射到整个游戏树上;统计树引导AI找到游戏树中最有趣的节点。节点的值由模拟决定。
MC方法:使用随机性来解决原则上可能确定性的问题。