状态空间搜索的结构和策略

发表于 更新于
介绍了深度优先搜索、广度优先搜索、迭代加深深度优先搜索等

人工智能与搜索

人工智能研究人员最根本的两个担忧

  • 知识表示（用语言捕获K）：以适合计算机操作的方式捕获知识
  • 搜索（解决问题的技巧）：系统地探索问题状态空间

状态空间表示 （SSR）：定义可能的状态；基于规则在这些状态之间进行转换：观察/动作

SSR用于模拟系统可能处于的不同配置；并找到达到解决方案的可能路径。

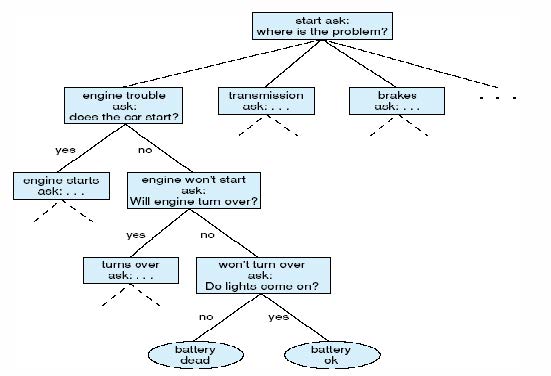
汽车诊断问题的状态空间描述。（就是搜索树罢）

符号人工智能

  • 问题状态：初始知识及其推论，例如 – 推理的中间步骤 – 棋盘游戏中的不同棋盘配置，例如国际象棋和围棋
  • 状态空间：问题状态的集合
  • 推理规则：从初始知识推断新知识

（然后用一堆经典问题举例，包括8数码、农夫过河、七桥问题，懒得贴上来了）

搜索

问题解决过程中的连续和替代阶段。

设计和实施搜索算法的成功程度取决于程序员分析问题的能力。

没有一种能解决所有问题的通用搜索算法，也称为“无免费午餐定理”

图

图由一组节点和一组弧组成

– 一组节点\(N_1\)、\(N_2\)、\(N_3\)、...、\(N_n\)...， – 一组连接节点对的弧 ## 状态空间搜索

状态空间由四元组\([N, A, S, GD]\)表示，其中：

– \(N\)是图中节点或状态的集合。这些对应于问题解决过程中的状态 – \(A\)是节点之间的弧（或链接）集合。这些对应于问题解决过程中的步骤 – \(S\)是\(N\)的非空子集，包含问题的起始状态 – \(GD\)是\(N\)的非空子集，包含目标状态或问题。\(GD\)中的状态使用以下任一方式描述： - 搜索中访问的状态的可测量属性 - 搜索中开发的路径的属性

练习\(1\)：两个水罐问题

你有一个空的\(4\)升水壶（\(J4\)）、一个空的\(3\)升水壶（\(J3\)）和一个可无限量供水的水龙头，以及一个排水管。目标是让\(J4\)中正好有\(2\)升水。 假设问题的状态表示为\((x,y)\)，其中\(x\)和\(y\)分别表示\(J4\)和\(J3\)的内容：\((J4,J3)\) 1. 写下初始状态和目标状态 2. 给出所需操作符的完整列表。两个这样的操作符是： 1. 从水龙头填充 J4 2. 将 J4 清空到排水管 3. 为任何一个解决方案绘制搜索图/树。

初始状态：\((0,0)\)，目标状态：\((2,i)\)，其中\(i=0,1,2,3\)

操作符：

  1. 从水龙头装满\(J4\)
  2. 清空\(J4\)至水槽
  3. 从水龙头装满\(J3\)
  4. 清空\(J3\)至水槽
  5. 将\(J4\)的水转移至\(J3\)
  6. 将\(J3\)的水转移至\(J4\)

（懒得画）

搜索策略

策略是通过选择图中节点扩展的顺序来定义的，从而实现目标。

策略的评估依据如下维度：

  • 完整性——如果存在解决方案，是否总能找到解决方案？
  • 时间复杂度——生成/扩展的节点数
  • 空间复杂度——内存中的最大节点数
  • 最优性——是否总能找到成本最低的解决方案？

时间和空间复杂度通过以下方式衡量 - b——搜索树的最大分支因子 - d——最小成本解决方案的深度 - m——状态空间的最大深度（可能是\(\infty\)）

  • 无知搜索 = 盲目搜索
  • 有知搜索 = 启发式搜索

数据驱动搜索

  • 从问题的给定事实和一组改变状态的合法动作或规则开始
  • 将规则应用于事实以产生新的事实，而规则又使用这些事实来生成更多新的事实
  • 继续，直到（我们希望！）它生成一条通往目标的路径
  • 这种方法有时称为前向链接

目标驱动搜索

  • 从目标开始
  • 看看哪些事实可以实现这个目标
  • 这些事实成为搜索的新目标或子目标
  • 搜索继续，通过连续的子目标向后工作，直到（我们希望！）它回到问题的事实
  • 这会找到从数据到目标的一系列动作或规则，尽管它是以相反的顺序进行的
  • 这种方法也称为后向链接

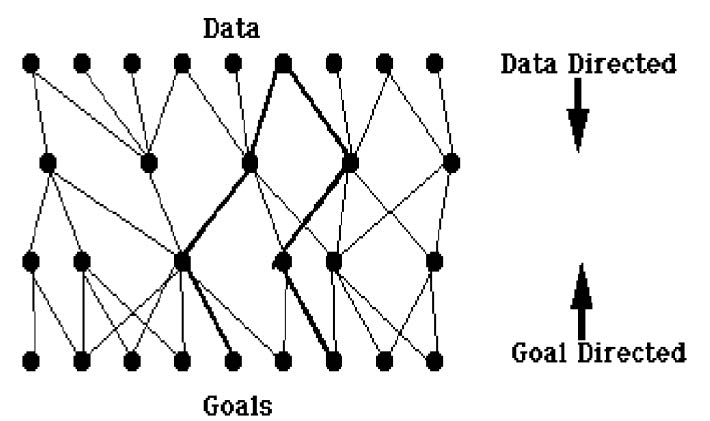
系统地搜索图

  • 图搜索用于探索状态空间以搜索某个节点（目标）
  • 它还可用于搜索两个节点之间的路径，检查图是否包含循环或是否连通等。

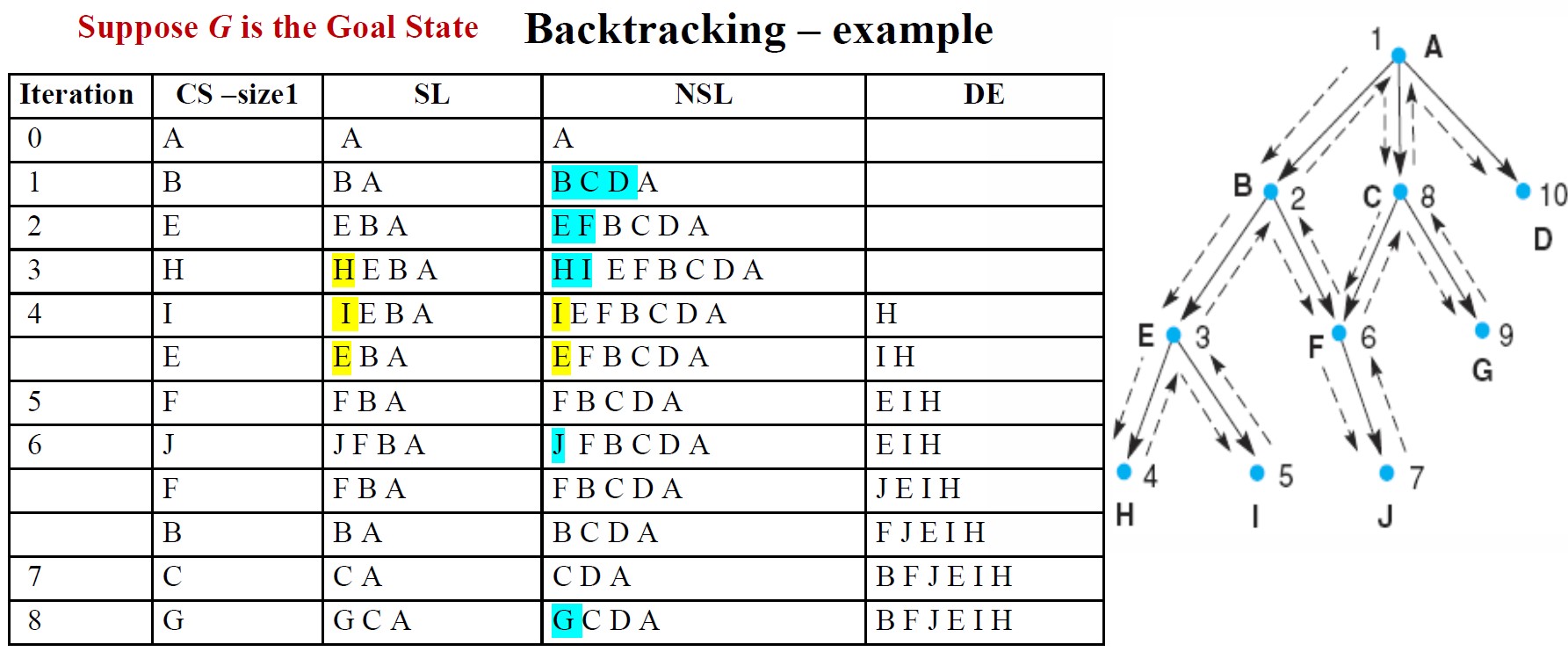
回溯搜索

  • 深度优先搜索CSP
  • 基本无信息搜索CSP

回溯算法

回溯符号

  • CS = 当前状态（当前正在考虑的状态）
  • SL = 状态列表（当前正在追求的路径中的状态列表。如果找到目标，SL 包含解决方案路径上状态的有序列表）
  • NSL = 新状态列表（新状态列表包含等待评估的节点，即尚未生成和搜索其后代的节点）
  • DE = 死胡同（后代未包含目标节点的状态列表。如果再次遇到这些状态，它们将被删除为 DE 的元素并被消除）
  • CS（当前状态）始终等于最近添加到 SL 的状态，并表示当前正在探索的解决方案路径的“边界”

回溯程序

  • 从起始状态开始
  • 沿着一条路径前进，直到到达目标或“死胡同”
  • 如果找到目标，则退出并返回解决方案路径
  • 如果到达死胡同，则“回溯”到路径上具有未检查兄弟节点（死胡同）的最新节点，并继续沿着其中一个分支前进

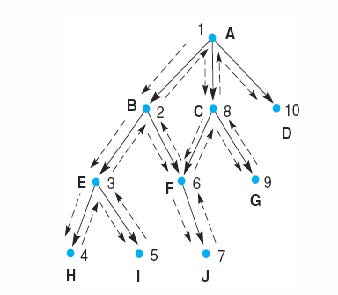
每个节点递归

  • 如果当前状态\(S\)不满足目标描述的要求，则生成其第一个后代\(S_\text{child‐1}\)，并对该节点递归应用回溯过程
  • 如果回溯在以\(S_\text{child‐1}\) 为根的子图中未找到目标节点，则对其兄弟\(S_\text{child‐2}\)重复该过程
  • 持续进行，直到某个子节点的后代是目标节点或所有子节点都已搜索完毕。

回溯中使用的主要思想

  1. 使用未处理状态列表（NSL）允许算法返回（回溯）到这些状态中的任何一个
  2. “坏”状态列表DE以防止算法重试无用状态
  3. 如果找到目标，则返回当前解决方案路径上的节点列表（SL）
  4. 明确检查这些列表中新状态的成员资格以防止循环
回溯样例

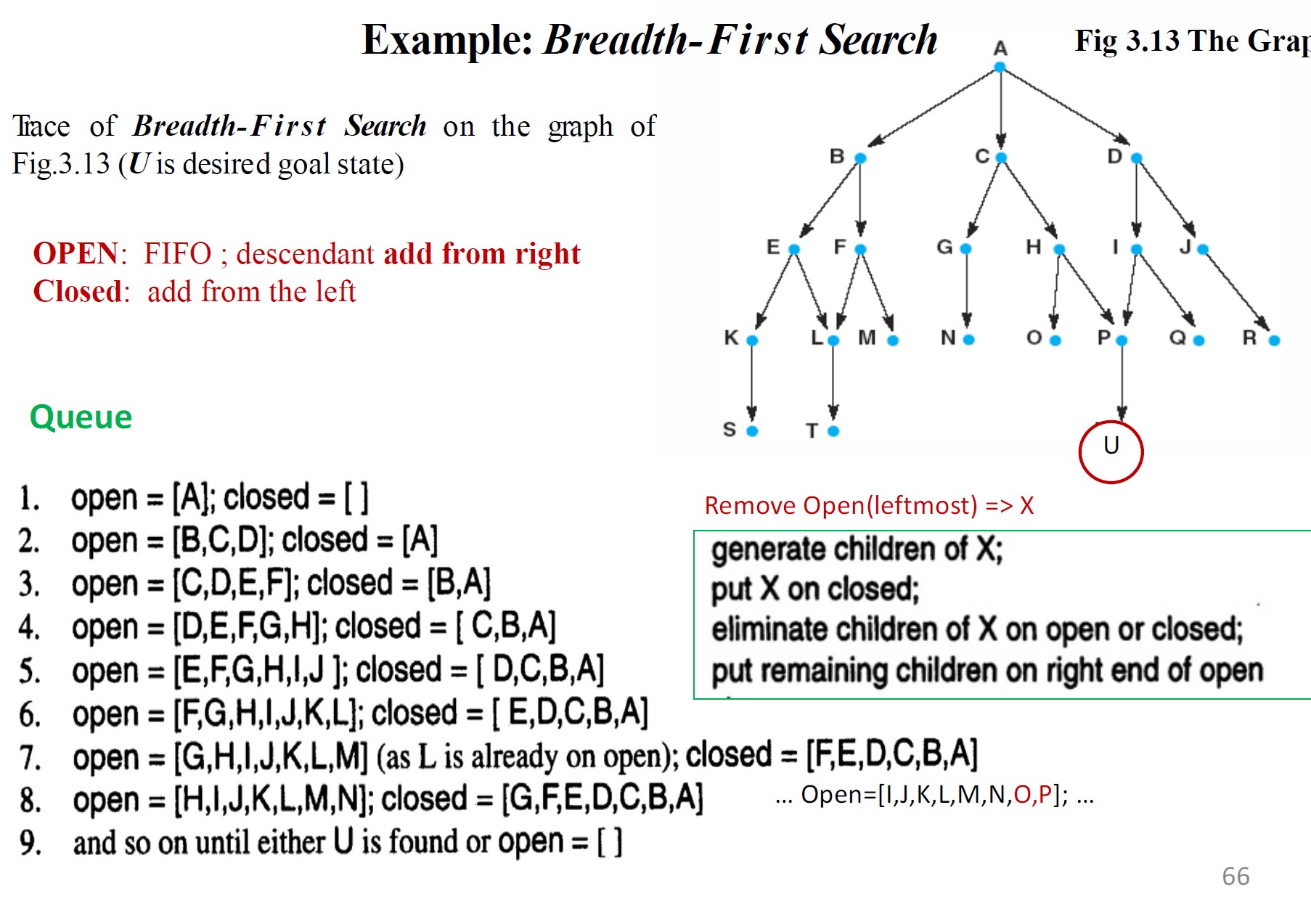
BFS：广度优先搜索

搜索空间以逐级方式探索，仅当给定级别上没有更多状态需要探索时，算法才会进入下一级

两个列表：

  • open - 已生成但其子状态尚未检查的状态
  • closed - 已检查的状态

祖先状态从open的左侧（开头）移除，后代状态从open的右侧（结尾）添加。open以队列或先进先出（FIFO）结构的形式维护。

BFS样例

广度优先搜索的优点：

  • 找到从起始状态到目标的最短路径

  • 永远不会陷入死胡同

  • 如果分支因子\(B\)（子节点的平均数量）很大，组合可能会阻止算法使用可用空间找到解决方案

  • 广度优先搜索的空间利用率（以开放状态的数量来衡量）是任何时间路径长度或第\(n\)级\(B^n\)个状态的指数函数

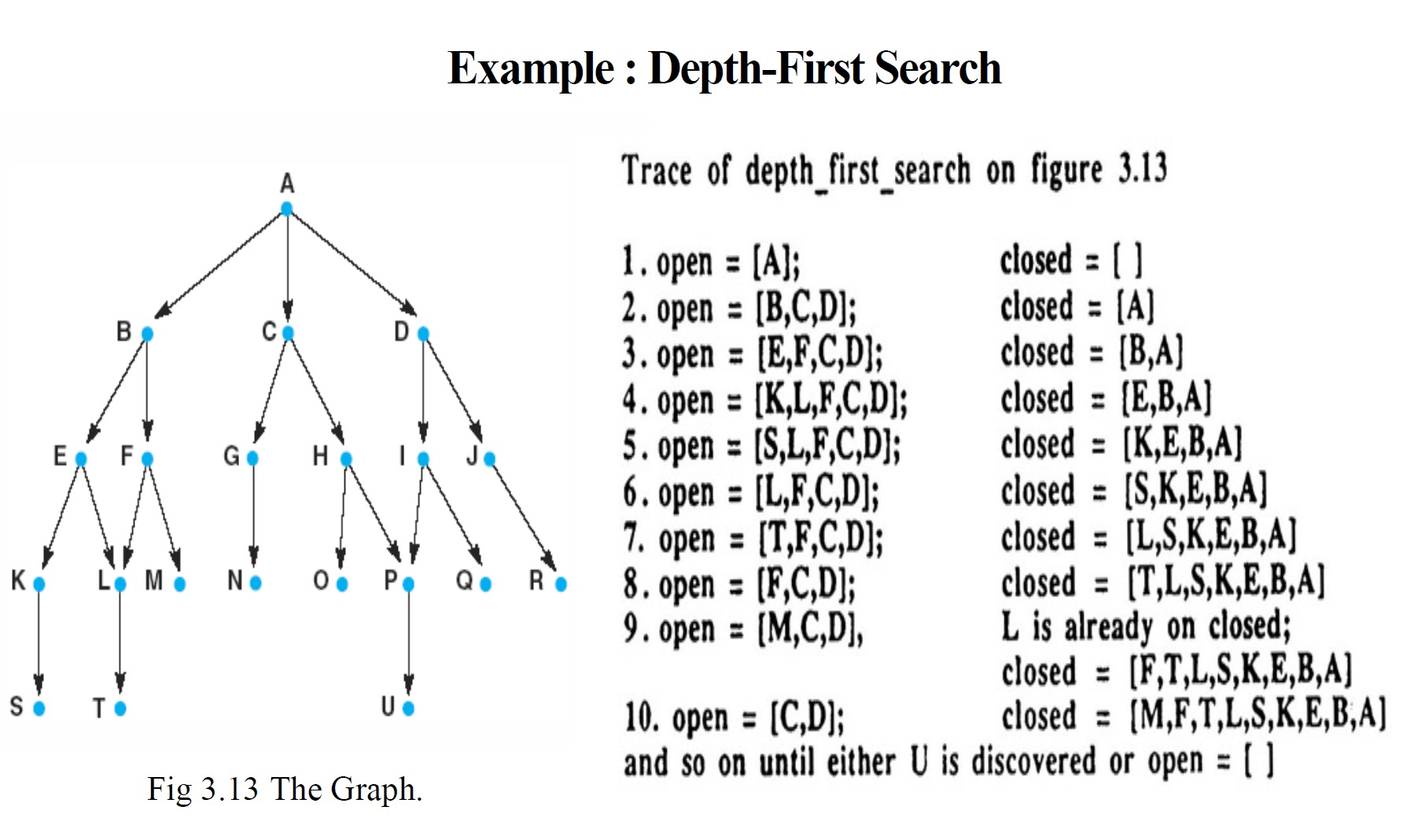
DFS：深度优先搜索

检查某个状态时，会先检查其所有子状态及其后代，然后再检查其兄弟状态。仅当找不到某个状态的其他后代时，才会考虑其兄弟状态

  • 后代状态从open的左侧（开头）添加和删除 - open以堆栈或后进先出（LIFO）结构维护
  • 以上述方式组织open会使搜索偏向最近生成的状态，从而使搜索具有深度优先顺序

两个列表：

  • open - 已生成但其子状态尚未检查的状态，类似于回溯中的 NSL
  • closed - 已检查的状态，回溯中的DE和SL的并集
DFS样例

深度优先搜索的优势

  • 深度优先搜索需要的内存较少，因为只有当前路径上的节点存储为\(B\times n\)。这与广度优先搜索形成对比，广度优先搜索中迄今为止生成的所有树都存储为\(B^n\)

  • 深度优先搜索会快速进入深度搜索空间。

  • 深度优先搜索可能会在图中“迷失”，错过到达目标的较短路径，甚至陷入无限长的路径中。

  • 深度优先搜索的空间使用量是路径长度的线性函数。在每个级别，open仅保留单个状态的子级或\(B\times n\)个状态以深入空间\(n\)级

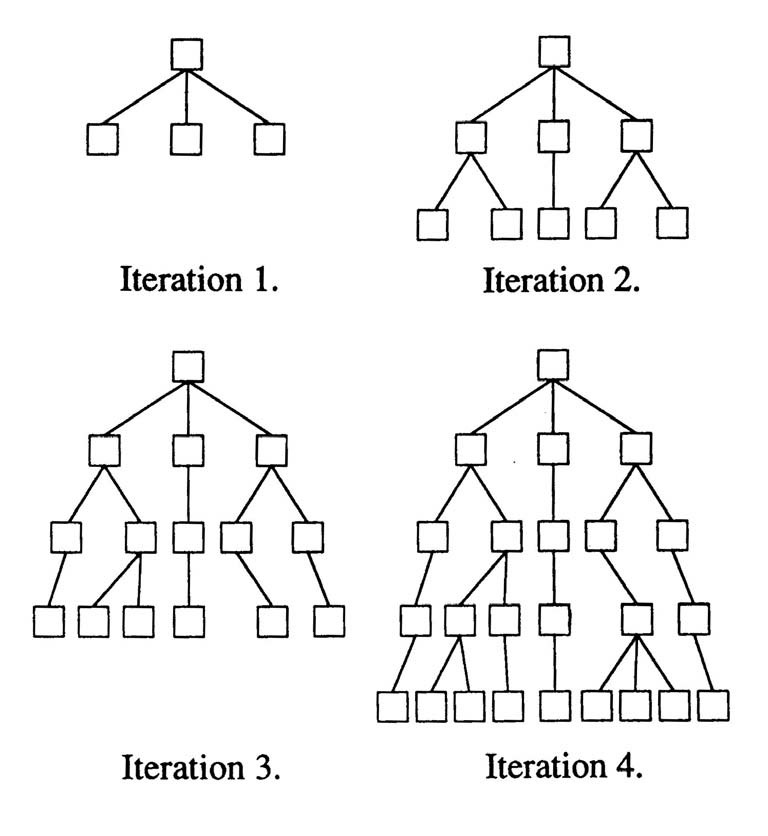
深度优先搜索与迭代深化：

  • 首先对空间进行深度优先搜索，深度界限为1
  • 如果找不到目标，则再进行一次深度优先搜索，深度界限为2。我们每次将深度界限增加一。
  • 每次迭代时，算法都会对当前深度界限进行完整的深度优先搜索。迭代之间不会保留有关状态空间的任何信息

  • 由于该算法以逐级方式搜索空间，因此保证找到到达目标的最短路径
  • 由于它在每次迭代中仅进行深度优先搜索，因此任何级别\(n\)的空间使用量都是\(B\times n\)，其中\(B\)是节点的平均子节点数

（空间复杂度：乐了；时间复杂度：不乐）

extraExcercise

\(1.\)

以下应用是否属于人工智能？请简要说明您的答案。

    1. 手机上的指纹识别
    1. 语音翻译
    1. 条形码扫描仪
    1. 仅基于关键词的W​​eb搜索引擎
    1. 适应交通状况的GPS导航设备
    1. 生物识别系统（仅存储信息）
    1. 可能是AI – NLP系统
    1. 信号处理
    1. 信息检索/数据库
    1. 可能是AI：实时；更智能

\(2.\)

一个人必须带着他的狐狸、鹅和一袋豌豆过河。每次航行，他的船只能载他自己或他自己和其中一件财物。假设在任何时候，一只无人看管的狐狸会吃掉鹅；一只无人看管的鹅会吃掉豌豆。我们需要设计一个状态空间问题解决系统来模拟这个人最终如何带着他所有的财物过河。

假设： - 每个状态以(L,R)的形式表示，其中L表示左岸的项目列表；R表示右岸的项目列表。 - 这个人和他的财产从右岸开始了他们的旅程。 - 可能包含在L或R中的项目有：人（M）；鹅（G）；狐狸（F）；豌豆（P）。

\(ⅰ\)

使用上面给出的过河问题的符号和假设写下初始状态和目标状态。

  • 初始状态：([], [M, G, F, P])
  • 目标状态：([M, G, F, P], [])

\(ⅱ\)

给出满足上述约束的系统所需操作/动作的列表

  • ①M单独走
  • ②带走G
  • ③带走F
  • ④带走P

\(ⅲ\)

开发部分状态空间，通过状态空间搜索解决问题。显示任何一个可能解决方案的搜索树，指出在每条边上应用的运算符。

...画图好麻烦。

\[\begin{aligned}&([],[M,G,F,P])\\\stackrel②\Longrightarrow&([M,G],[F,P])\\\stackrel①\Longrightarrow&([G],[M,F,P])\\\stackrel③\Longrightarrow&([M,G,F],[P])\\\stackrel②\Longrightarrow&([F],[M,G,P])\\\stackrel④\Longrightarrow&([M,F,P],[G])\\\stackrel①\Longrightarrow&([F,P],[M,G])\\\stackrel②\Longrightarrow&([M,G,F,P],[])\end{aligned}\]

\(3.\)

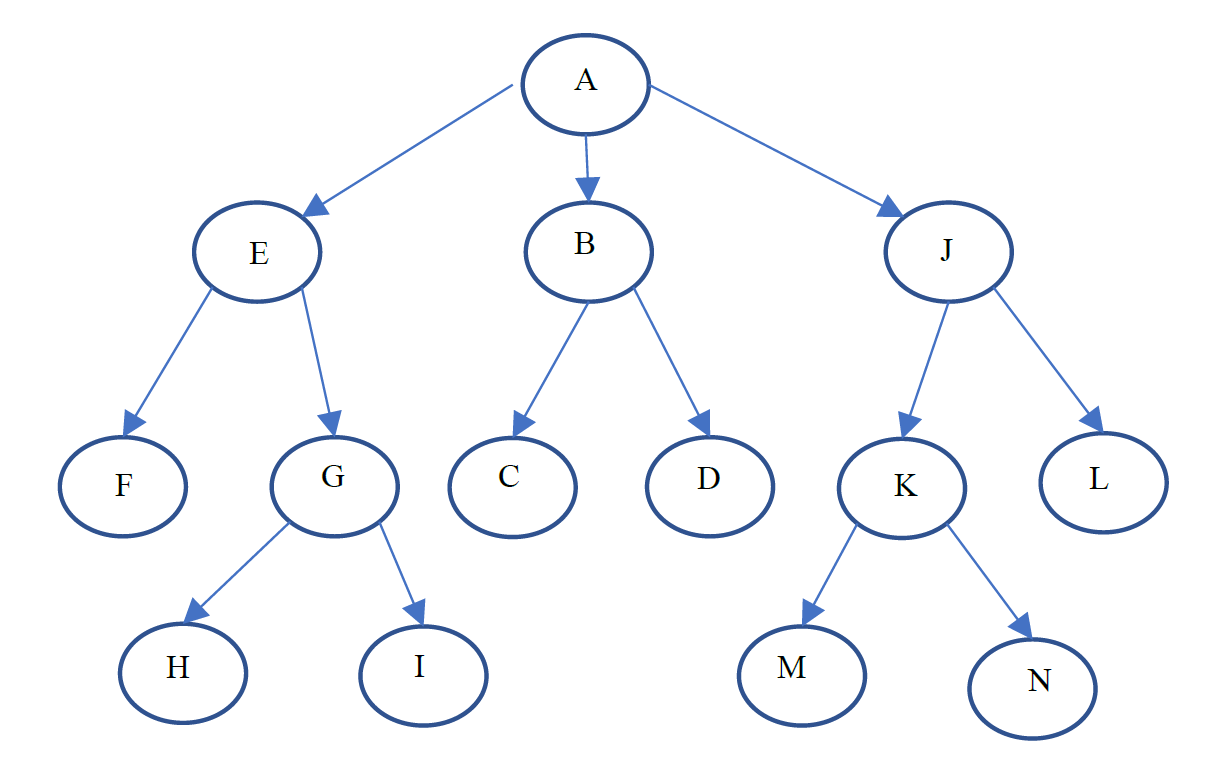
假设起始节点为 A，目标节点为 I。提供下图所示节点的搜索顺序，分别为深度优先搜索 (DFS)、广度优先搜索 (BFS)、迭代深化搜索 (IDS)（起始深度 = 1）。显示每一步中开放和封闭列表中的更新。

DFS

Open Closed
A
E, B, J A
F, G, B, J E, A
G, B, J F, E, A
H, I, B, J G, F, E, A
I, B, J H, G, F, E, A

BFS

Open Closed
A
E, B, J A
B, J, F, G E, A
J, F, G, C, D B, E, A
F, G, C, D, K, L J, B, E, A
G, C, D, K, L F, J, B, E, A
C, D, K, L, H, I G, F, J, B, E, A

IDS

这怎么写

只能写每一步罢

Step 遍历顺序
1 A
2 A E B J
3 A E F G B C D J K L
4 A E F G H I