直观理解视觉对象识别:从匹配到分类再到机器学习
直观尼玛,能不能留在国内祸害国内学生
模板匹配、距离和相似度
模板匹配指的是通过模板图像与测试图像之间的比较,找到测试图像上与模板图像相似的部分,这是通过计算模板图像与测试图像中目标的相似度来实现的,可以快速地在测试图像中定位出预定义的目标。匹配的主要思路是使用一个目标原型,根据它创建一个模板,在测试图像中搜索与该模板图像最相似的目标,并寻找与该模板的均值或方差最接近的区域。 --CSDN
系统如何识别查询对象\(F\)?
系统在其图库/数据库中有\(c\)个不同的对象\(G_j,j=1,2,\cdots,c\)。
给定一个未知的查询对象\(F\),系统需要识别/辨别它是否来自与图库对象\(G_j\)相同的源,\(j=1,2,\cdots,c\)。
\[G_k=\argmin_j\left\lVert F-G_j\right\rVert\]
被称为模板匹配,它将未知查询对象与每个已知图库对象或模板对象进行比较,以找到匹配的图库对象。
这需要计算两个对象之间的距离或相似度
\[d_j=\left\lVert F-G_j\right\rVert,\quad \text{for}\ j=1,2,\cdots,c\]
灰度图像所表示的视觉对象由不同\(x\)和\(y\)位置的不同亮度指定。因此,灰度图像是\(x\)和\(y\)的函数\(f(x,y)\),可以用矩阵表示。
两个大小为\(p\times q\)的图像\(f(x,y)\)和\(g(x,y)\)表示的两个视觉对象\(F\)和\(G\)之间的Euclidean距离定义为(注意,为了符号简单起见,省略了平方根。)
\[d=\lVert F-G\rVert=\sum_{y=1}^q\sum_{x=1}^p\left[f(x,y)-g(x,y)\right]^2\]
为了方便起见,我们将\(p\)乘\(q\)矩阵\(F\)和\(G\)转换为\(n\)维列向量\(\mathbf f\)和\(\mathbf g\),\(n=pq\)。例如,\(p=q=3\),则\(n=3\times3=9\):

然后,我们可以方便地将(平方)欧几里得距离表示为:
\[d=\lVert F-G\rVert=\lVert\mathbf f-\mathbf g\rVert^2=(\mathbf f-\mathbf g)^\intercal(\mathbf f-\mathbf g)\]
这就是方便的向量差、转置和乘法。
然而,两幅图像之间的欧几里得距离真的能体现两个视觉对象的相似性吗?
计算以下两幅图像的欧几里得距离:

我们有
\[\begin{aligned}\mathbf f&=\left[\begin{array}{ccccccccc}1&1&1&1&0&1&0&0&0\end{array}\right]^\intercal\\\mathbf g&=\left[\begin{array}{ccccccccc}100&100&100&100&10&100&10&10&10\end{array}\right]^\intercal\end{aligned}\]
虽然两幅图像显示的是相同的三角形图案,但欧几里得距离却很大,只是亮度和对比度不同。如何解决这个问题?
我们将图像标准化为零均值和单位方差。
由\(\mathbf f=\left[\begin{array}{ccccccccc}1&1&1&1&0&1&0&0&0\end{array}\right]^\intercal\),可以得到平均值\(m_\mathbf f=\frac59\)。因此我们有集中向量
\[\begin{aligned}\mathbf f_c&=\mathbf f-m_\mathbf f\\&=\left[\begin{array}{ccccccccc}1-\frac59&1-\frac59&1-\frac59&1-\frac59&0-\frac59&1-\frac59&0-\frac59&0-\frac59&0-\frac59\end{array}\right]^\intercal\\&=\left[\begin{array}{ccccccccc}\frac49&\frac49&\frac49&\frac49&-\frac59&\frac49&-\frac59&-\frac59&-\frac59\end{array}\right]^\intercal\end{aligned}\]
图像的标准差或矢量的长度是
\[\lVert\mathbf f_c\rVert=\sqrt{\frac19\mathbf f_c^\intercal\mathbf f_c}=\sqrt{\frac19\left(\left(\frac49\right)^2+\left(\frac49\right)^2+\cdots\right)}=\frac{\sqrt{20}}9\]
我们将图像归一化为零均值和单位方差/长度
\[\mathbf f_n=\frac{\mathbf f_c}{\lVert\mathbf f_c\rVert}=\frac1{\sqrt{20}}\left[\begin{array}{ccccccccc}4&4&4&4&-5&4&-5&-5&-5\end{array}\right]^\intercal\]
注意\(\mathbf f_n\)具有零均值和单位方差。
对\(\mathbf g\)重复相同的过程,计算可得
\[\mathbf g_n=\frac1{\sqrt{20}}\left[\begin{array}{ccccccccc}4&4&4&4&-5&4&-5&-5&-5\end{array}\right]^\intercal=\mathbf f_n\]
这样,归一化图像的欧几里得距离
\[d_n=(\mathbf f_n-\mathbf g_n)^\intercal(\mathbf f_n-\mathbf g_n)=0\]
尝试另一个图像,\(\mathbf h=\left[\begin{array}{ccccccccc}1&2&3&4&2&1&2&3&4\end{array}\right]^\intercal\),可以得到\(d_n=(\mathbf f_n-\mathbf h_n)^\intercal(\mathbf f_n-\mathbf h_n)\gg0\)
因此,\(d_n\)可以用作模板匹配的距离
我们定义相关系数:
\[\gamma=\mathbf f_n^\intercal\mathbf g_n=\frac{(\mathbf f-m_\mathbf f)^\intercal(\mathbf g-m_\mathbf g)}{\lVert\mathbf f_c\rVert\lVert\mathbf g_c\rVert}\]
则对于这两幅图像\(F\)和\(G\),我们有\(\gamma=1\)。
\(F\)或\(G\)与\(H\)的相关系数将产生\(\gamma\lt1\)。事实上,对于所有图像,\(−1\le\gamma\le1\)。
因此,\(\gamma\)可以用作模板匹配的相似度
从模板匹配到分类
我们用一个包含所有像素灰度值的\(n\)维列向量来表示图像对象,一个向量元素对应一个像素,从\(p\)乘\(q\)矩阵到\(n\)维向量,\(n=pq\)。
\(n\)维向量是\(n\)维空间中的一个点。为了形象化地展示这个过程,取\(n=c=2\)并使用距离,如图所示。
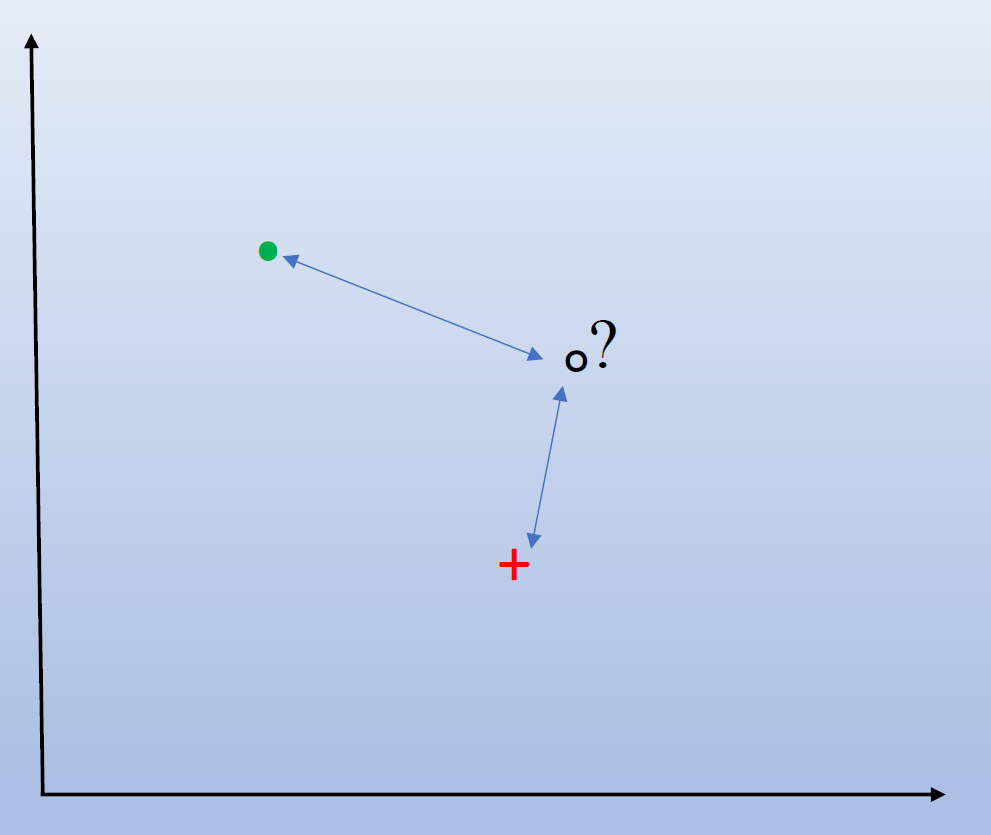
然而,一个物体有很多变体,仅用一张图片来表示一个物体是不够的。每个对象应该由多幅图像来表示。因此,每个对象被称为一个类,每个图像被称为该类的一个样本。
因此,将未知查询对象识别/认定为\(c\)个已知图库对象之一就转化为将其归类到\(c\)个类之一。

如何将未知查询对象归类为\(c\)个已知类之一?
(老师讲的一坨,可以去看视频:【小萌五分钟】机器学习 | K近邻算法 KNN)
第一最近邻(NN)分类器:
用\(D^n=\{\mathbf x_1,\cdots,\mathbf x_2\}\)表示一组带标签的原型或训练样本
让\(\mathbf x^*\)成为最接近\(\mathbf x\)的原型
然后,用于对\(\mathbf x\)进行分类的最近邻(NN)规则是为其分配与\(\mathbf x^*\)相关的标签
更正式地说,如果我们有一组带标签的训练样本\(\{(\mathbf x_1,\theta_1),\cdots,(\mathbf x_n,\theta_n)\}\),其中每个\(\theta_i\)都是标签\(\omega_1,\cdots,\omega_c\)之一,那么NN决策规则就是
\[\alpha_{\text{nn}}=\theta_k:k=\argmin_i\lVert\mathbf x-\mathbf x_i\rVert\]
NN规则的推广
\(k_n\)最近邻规则(k-NN):给定一组训练样本\(\{\mathbf x_1,\cdots,\mathbf x_n\}\)和一个测试点\(\mathbf x\),找到最接近\(\mathbf x,\mathbf x_1^*,\cdots,\mathbf x_k^*\)的\(k\)个训练点。收集与\(\theta_1^*,\cdots,\theta_k^*\)相关的标签,并将\(\mathbf x\)归类为在\(\theta_1^*,\cdots,\theta_k^*\)中具有最多代表的类。
换句话说,分类是通过在\(\mathbf x\)的\(k\)个最近邻中进行多数投票来执行的
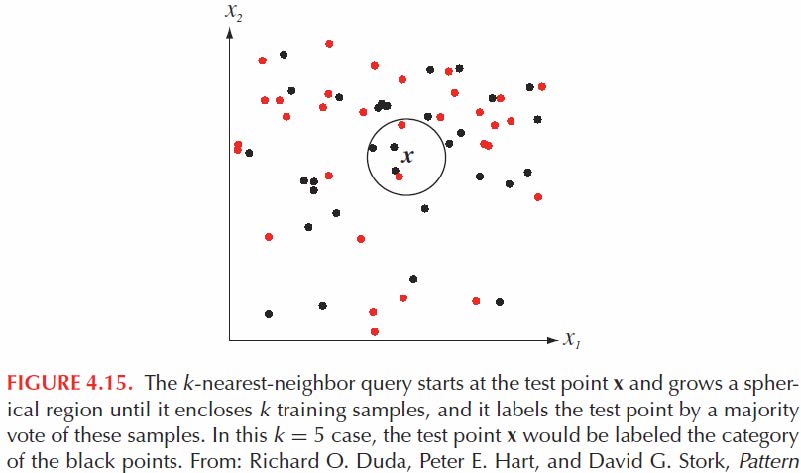
然而,有些类别可能有数千或数百万个样本。将查询样本与每个训练样本进行比较非常繁琐。NN分类器也会过度拟合训练数据或泛化能力较差。如何解决这些问题?
一种解决方案是最小距离分类器,它比较查询样本与每个类均值向量\(\mathbf\mu_j\)的距离。
给定\(c\)类的\(q\)个\(n\)维训练样本\(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_q\)
\(\omega_j\)类的训练样本数量为\(q_j,\ j=1,2,\cdots,c\)。\(\omega_j\)类的均值向量计算如下
\[\mu_j=\frac1{q_j}\sum_{\mathbf x_i\in\omega_j}\mathbf x_i\]
在接收到查询样本\(\mathbf x\)之前,机器会从训练数据中计算一些参数。这就是机器学习。
最小Euclidean距离分类器对未知查询样本\(\mathbf x\)进行分类:
\[\omega_k=\argmin_j(\mathbf x-\mu_j)^\intercal(\mathbf x-\mu_j)\]
然而,仅仅使用类别均值向量来表示一个类别并不复杂。通过一维示例可视化该问题:
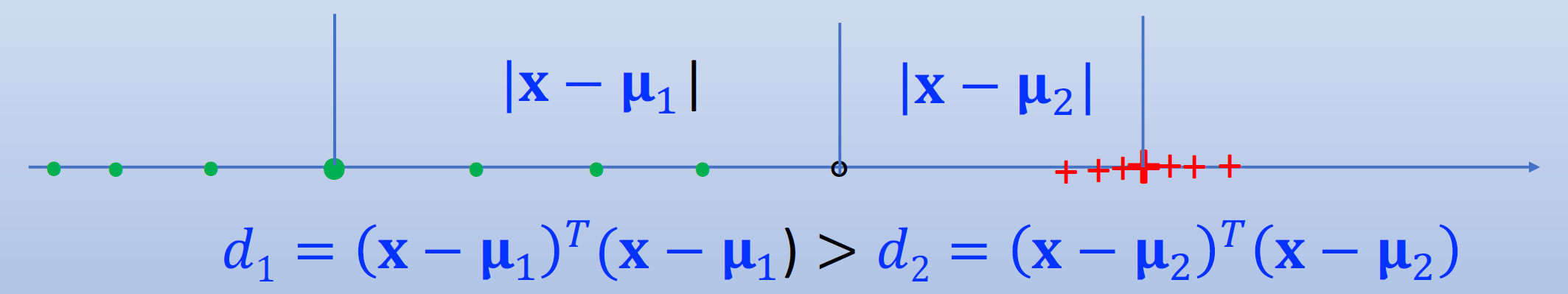
\(\mathbf x\)是否应该被归类为第2类(红色)?很可能是错的!问题是什么?
(下面开始讲Mahalanobis距离,讲得仍然是一坨,请看博客:Mahalanobis(马哈拉诺比斯)距离)
以一维数据为例,除了类均值之外,我们还应该考虑类标准差或方差。
一种解决方案是通过类标准差对欧几里得距离进行归一化,或者通过类方差对平方欧几里得距离进行归一化。
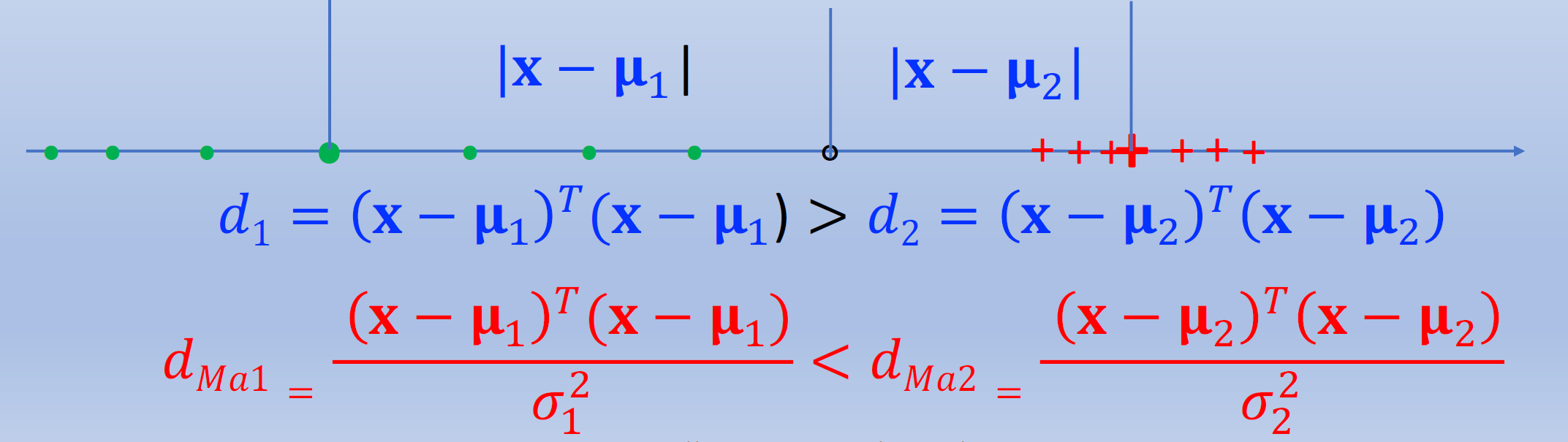
然而,对于多维数据,除了数据向量每个元素的均值和方差之外,我们还有数据向量不同元素之间的协方差。
给定\(c\)类的\(q\)个\(n\)维训练样本\(\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_q\)
\(\omega_j\)类的训练样本数量为\(q_j,\ j=1,2,\cdots,c\)。\(w_j\)类的均值向量和协方差矩阵计算如下
\[\mu_j=\frac1{q_j}\sum_{\mathbf x_i\in\omega_j}\mathbf x_i\]
\[\begin{aligned}\Sigma_j&=\frac1{q_j}\sum_{\mathbf x_i\in\omega_j}(\mathbf x_i-\mu_j)(\mathbf x_i-\mu_j)^\intercal\\&=\frac1{q_j}\sum_{\mathbf x_i\in\omega_j}\mathbf x_i\mathbf x_i^\intercal-\mu_j\mu_j^\intercal\end{aligned}\]
为了使距离通过数据变化进行归一化,Euclidean距离的平方:
\[d_{\text{Eu}j}=\lVert\mathbf x-\mu_j\rVert^2=(\mathbf x-\mu_j)^\intercal(\mathbf x-\mu_j)\]
由协方差矩阵的逆加权
\[d_{\text{Ma}j}=(\mathbf x-\mu_j)^\intercal\Sigma_j^{-1}(\mathbf x-\mu_j)\]
称为(平方)马哈拉诺比斯(Mahalanobis)距离。
如果每个类的数据都遵循正态分布,则最小马哈拉诺比斯距离分类器是最佳分类器。
该图显示了二维情况下“红色”类和“蓝色”类的数据变化或分布。
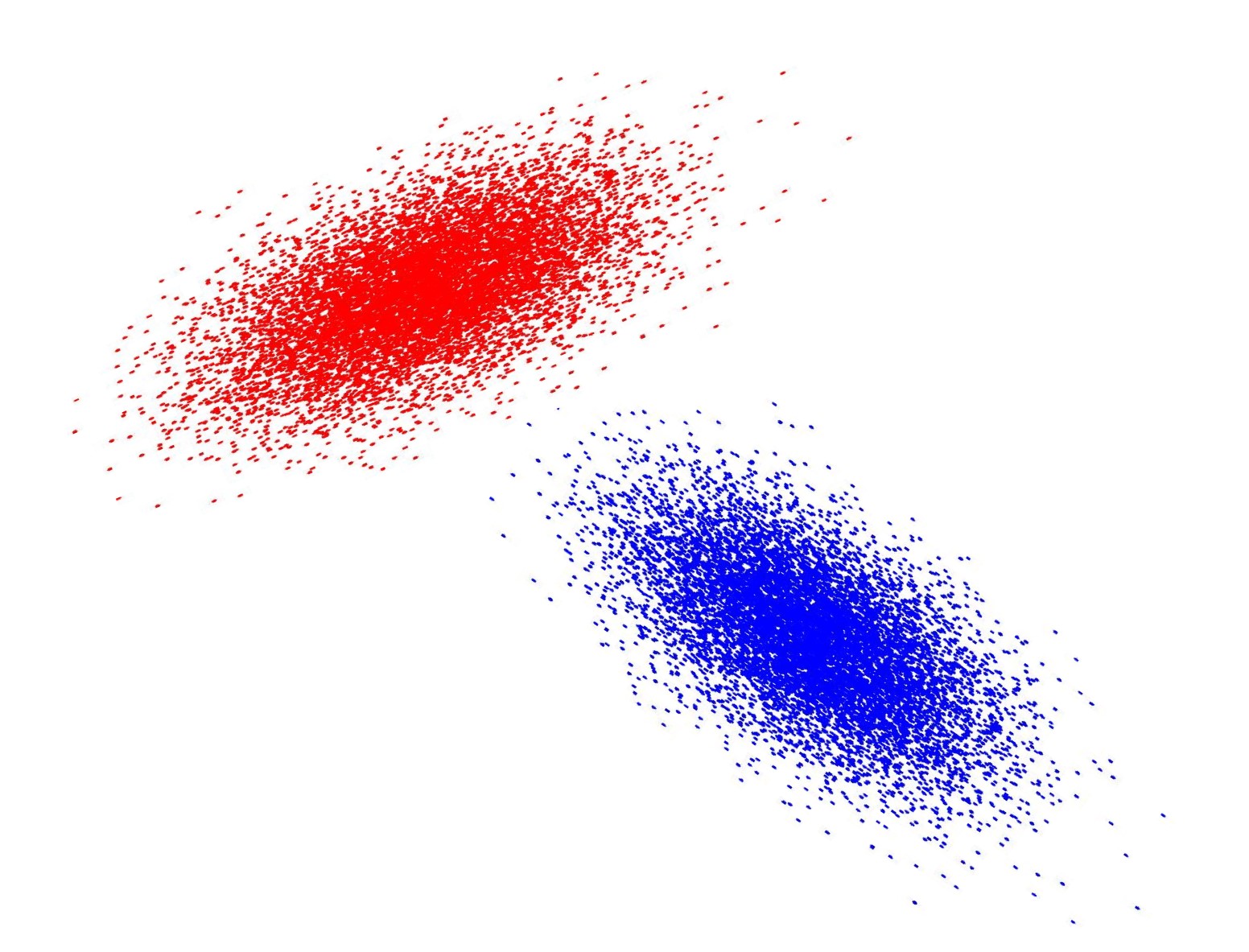
数据变化或分布的形状和大小由协方差矩阵决定。
协方差矩阵所形成的椭圆上的所有点到椭圆中心的距离都相同。它与正态分布的轮廓一致
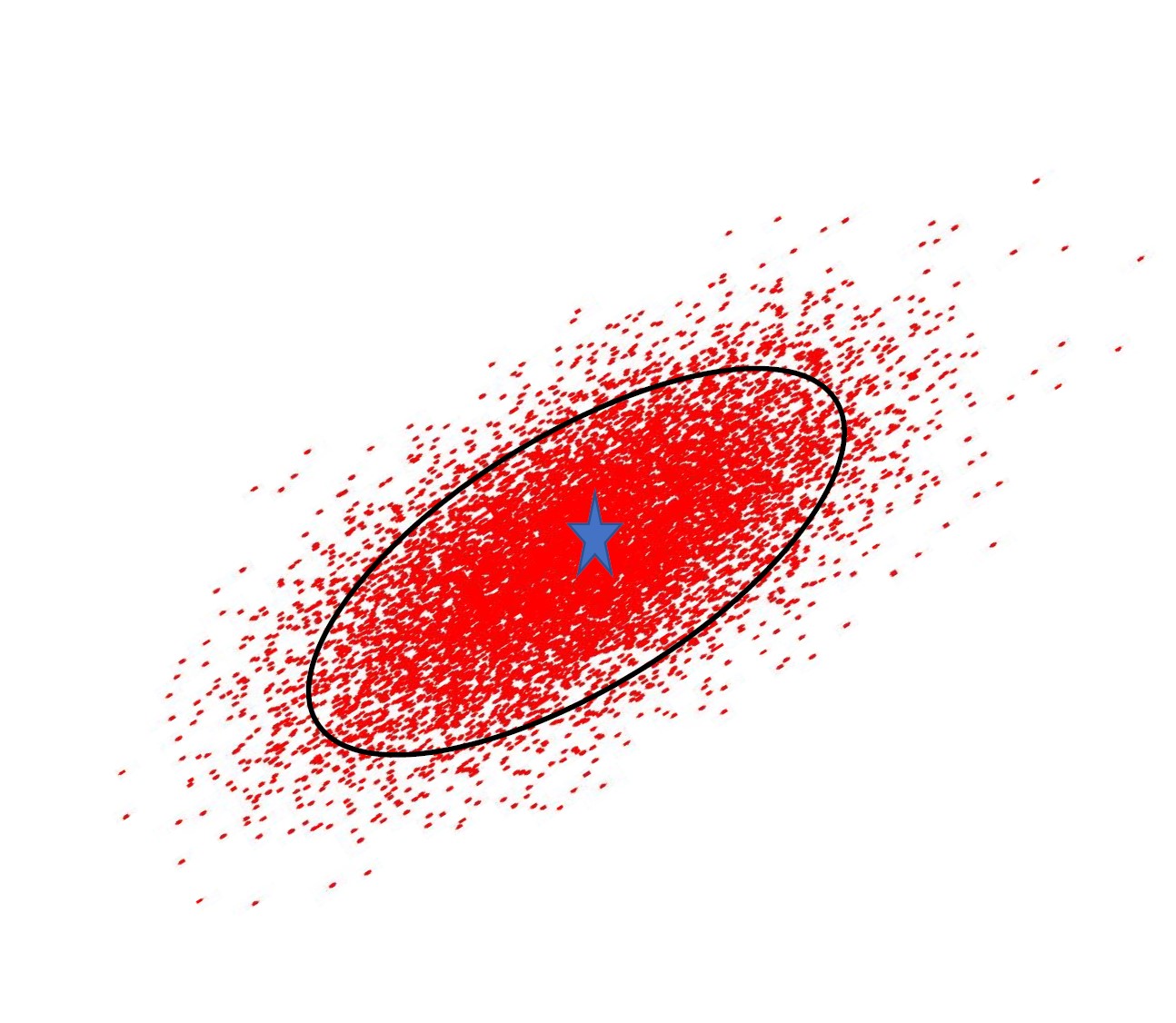
如果我们将集中训练样本表示为
\[\tilde{\mathbf x}_i=\mathbf x_i-\mu_j\]
并将某一类的训练样本的所有列向量放入一个矩阵中:
\[\mathbf X_j=\left[\begin{array}{cccccc}\tilde{\mathbf x}_1&\tilde{\mathbf x}_2&\cdots&\tilde{\mathbf x}_i&\cdots&\tilde{\mathbf x}_{q_j}\end{array}\right]\]
那么我们可以这样表达:
\[\Sigma_j=\frac1{q_j}\sum_{\mathbf x_i\in\omega_j}(\mathbf x_i-\mu_j)(\mathbf x_i-\mu_j)^\intercal=\frac1{q_j}\mathbf X_j\mathbf X_j^\intercal\]
对于某些分类问题,我们可能有大量的类别,但每个类别的训练样本数量很少。由单个类别的少量训练样本计算出的协方差矩阵非常不可靠。因此,我们对所有类别的协方差矩阵进行平均,称为池化类别协方差矩阵,也称为类内散度矩阵。
\[\Sigma^{\mathrm w}=\frac1q\sum_{j=1}^cq_j\Sigma_j\]
我们已经看到,协方差矩阵代表了数据变化或分布的丰富信息。
除了
\[\Sigma_j=\frac1{q_j}\mathbf X_j\mathbf X_j^\intercal\]
\[\Sigma^{\mathrm w}=\frac1q\sum_{j=1}^cq_j\Sigma_j=\mathbf S^{\mathrm w}\]
我们定义更多的协方差矩阵为
\[\mathbf S^b=\frac1q\sum_{j=1}^cq_j(\mu_j-\mu)(\mu_j-\mu)^\intercal\]
\[\mathbf S^t=\frac1q\sum_{i=1}^c(\mathbf x_i-\mu)(\mathbf x_i-\mu)^\intercal=\frac1q\mathbf{XX}^\intercal\]
\(\mathbf X\)是集中于\(\mu=\frac1q\sum_{i=1}^q\mathbf x_i\)的所有样本的数据矩阵。
这些协方差矩阵具有以下关系:
\[\mathbf S^t=\mathbf S^{\mathrm w}+\mathbf S^b=\frac1q\sum_{j=1}^cq_j\Sigma_j+S^b\]
\(\mathbf S^t\)称为数据总散度矩阵,\(\mathbf S^{\mathrm w}\)称为类内散度矩阵,\(\mathbf S^b\)称为类间散度矩阵。
WRNM