数据挖掘简介与关联分析

发表于 2024-09-08 更新于 2024-09-14

讲解了数据挖掘重要算法Apriori算法和FP-Growth算法等。

数据挖掘简介

什么是数据？

数据：数据对象及其属性的集合

属性是对象的属性或特征。例如：人的眼睛颜色、温度等。属性也称为变量、字段、特性或特征

属性的集合描述一个对象，对象也称为记录、点、案例、样本、实体或实例

数据矩阵

如果数据对象具有相同的一组固定的数字属性，则可以将数据对象视为多维空间中的点，其中每个维度代表一个不同的属性

此类数据集可以用一个\(m\times n\)矩阵表示，其中有\(m\)行，每个对象一行，\(n\)列，每个属性一列

事务数据（transaction data）

一种特殊类型的记录数据，其中

每条记录（事务）涉及一组项目。
例如，考虑一家杂货店。客户在一次购物过程中购买的一组产品构成交易，而购买的单个产品则是项目。

图形数据、基因组序列数据

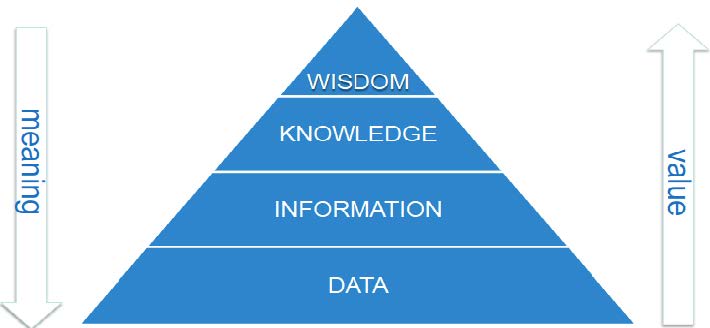
数据、信息、知识

数据：任何可被计算机处理的事实（单词）、数字或文本。
信息：所有这些数据之间的模式、关联或关系可以提供信息。
知识：信息可以转化为有关历史模式和未来趋势的知识。

什么是数据挖掘？

从数据中发现知识：从海量数据中提取有趣的（非平凡的、隐含的、以前未知的和潜在有用的）模式或知识。

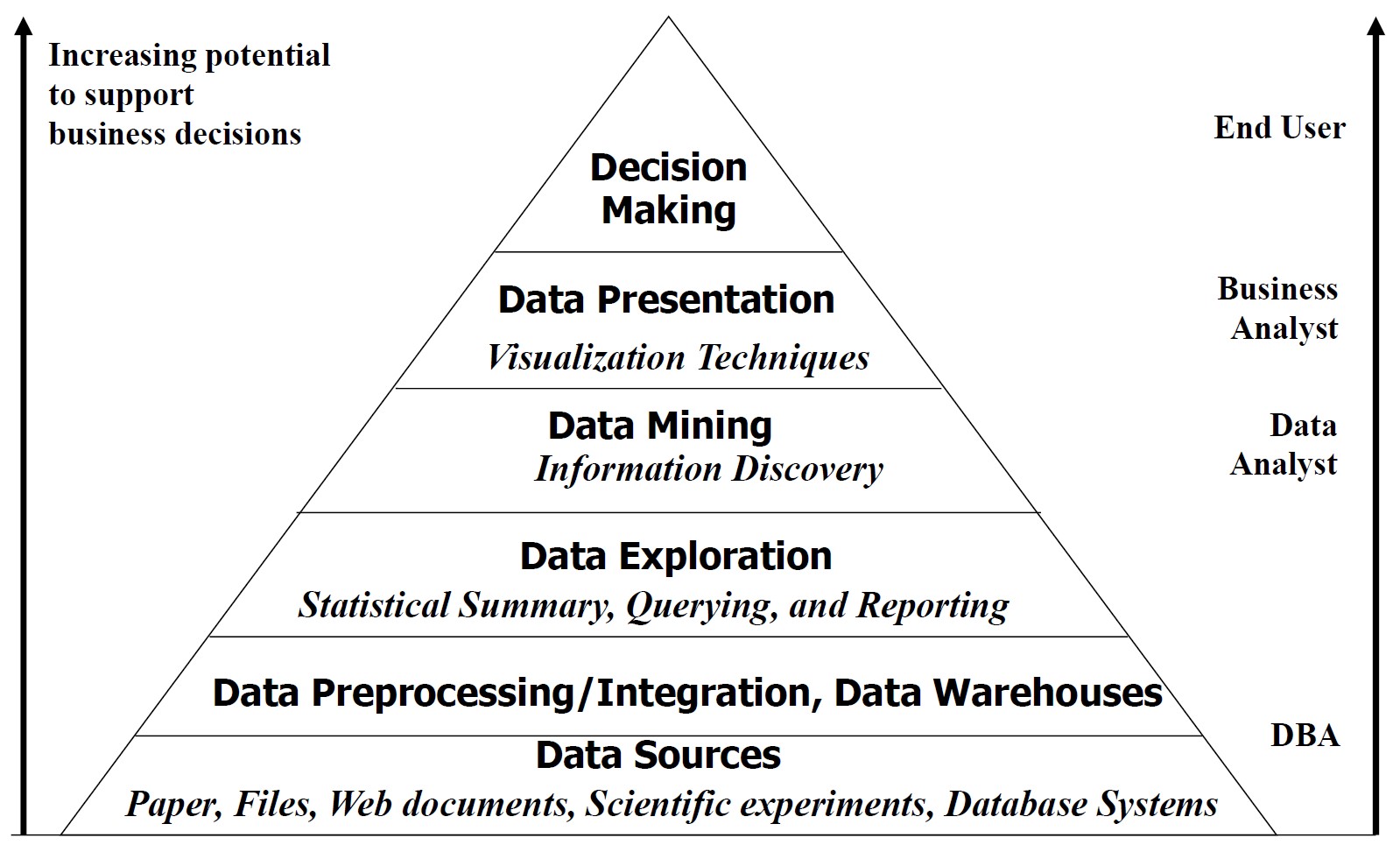
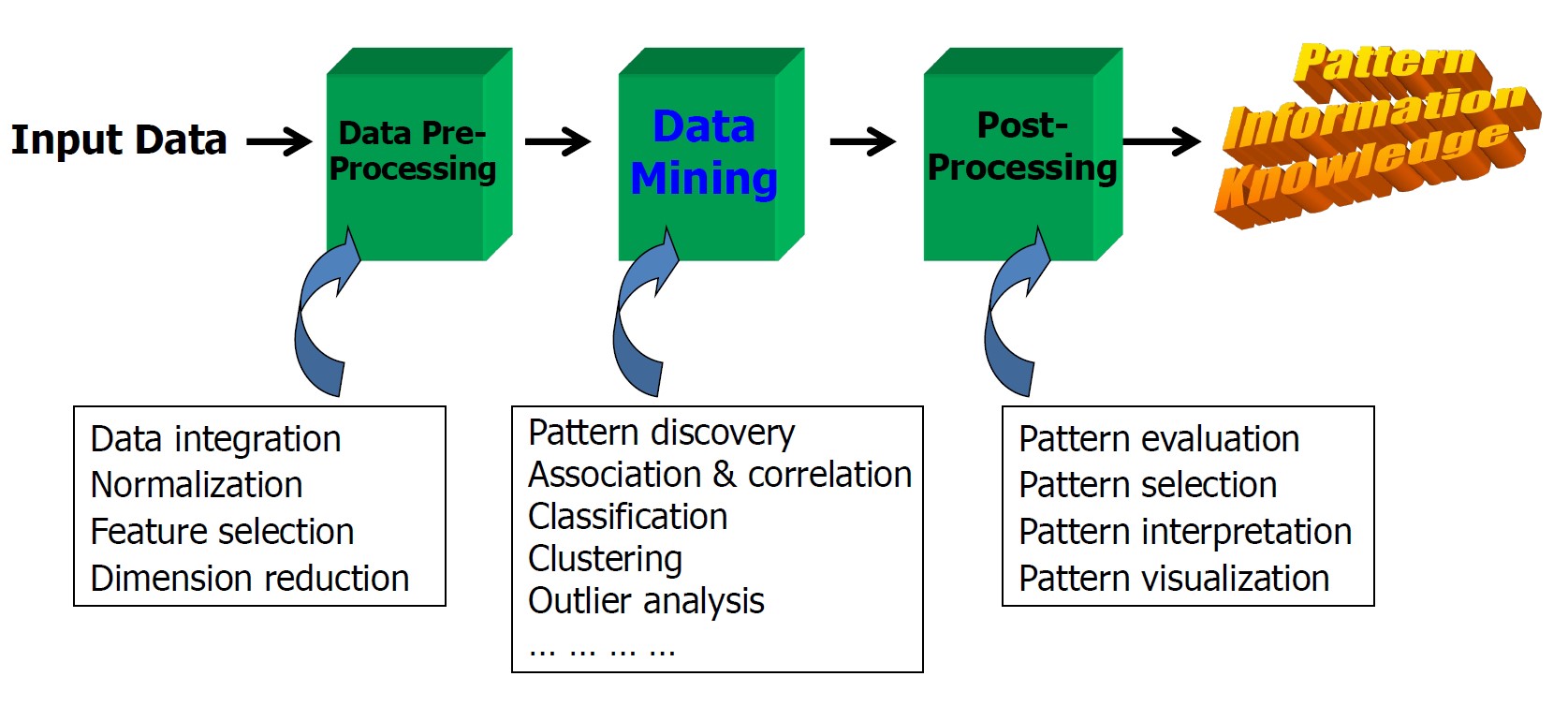
数据挖掘是数据库中知识发现 (KDD) 的关键步骤
数据预处理通常是整个知识发现过程中最费力和最耗时的步骤
后处理可确保仅保留有效且有用的结果并进一步利用

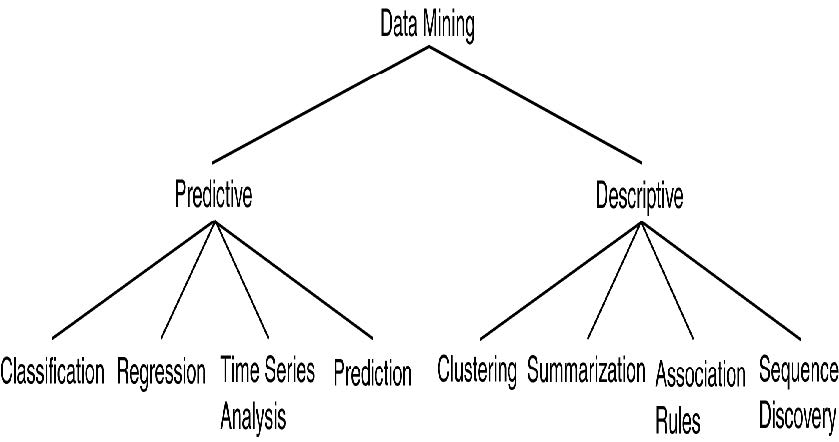
数据挖掘的类型=关键功能

概括（Generalization）
- 特征化和判别
- 多维概念描述与判别
- 概括、总结和对比数据特征
关联（相关性和因果关系）分析（Association analysis）
分类和预测（Classification and Prediction）
- 构建模型（函数）来描述和区分类别或概念，以便进行未来预测
- 演示：决策树、分类规则、神经网络
- 预测一些未知或缺失的数值
聚类分析（Cluster analysis）
- 类别标签未知：将数据分组以形成新类别，例如，将房屋聚类以查找分布模式
- 最大化类内相似性并最小化类间相似性
异常值分析（Outlier analysys）
- 处理不符合数据一般行为的数据对象
- 在欺诈检测、罕见事件分析中很有用

挖掘哪些类型的数据？

关系数据库
数据仓库
事务数据库
高级数据库和信息存储库
- 对象关系数据库
- 空间和时间数据
- 时间序列数据
- 流数据
- 多媒体数据库
- 异构和遗留数据库
- 文本数据库和WWW
- 社交媒体
- 云数据
- …

数据挖掘应用

市场或业务数据分析和决策支持
- 市场分析和管理
  - 目标营销、客户关系管理 (CRM)、市场篮子分析、交叉销售、市场细分
- 风险分析和管理
  - 预测、客户保留、改进承保、质量控制、竞争分析
- 欺诈检测和异常模式（异常值）检测
其他应用
- 文本挖掘（新闻组、电子邮件、文档）和Web挖掘
- 医疗和DNA/生物数据分析
- 社交媒体和多媒体数据分析
- 教育数据分析
- 医疗保健
- …

架构：典型的数据挖掘系统

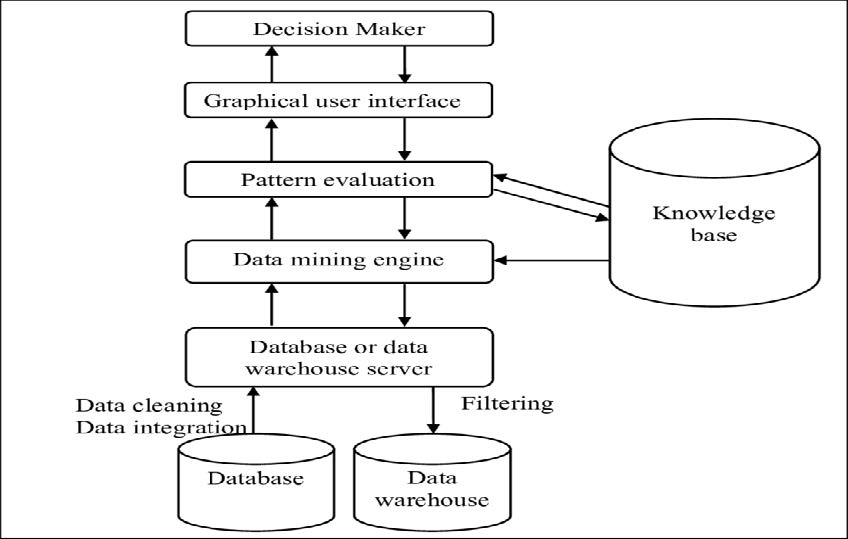
数据挖掘中的主要问题

挖掘方法
- 从各种数据类型（例如，生物、网络）中挖掘不同类型的知识
- 性能：效率、有效性和可扩展性
- 模式评估：兴趣度问题
- 背景知识的整合
- 处理噪声和不完整数据
- 并行、分布式和增量挖掘方法
- 将发现的知识与现有知识集成：知识融合
用户交互
- 数据挖掘查询语言和临时挖掘
- 数据挖掘结果的表达和可视化
- 多层次抽象知识的交互式挖掘
应用和社会影响
- 领域特定数据挖掘和隐形数据挖掘
- 保护数据安全、完整性和隐私

1998年，美国连锁超市沃尔玛 (Wal-Mart) 知道，购买芭比娃娃 (每 20 秒售出一个) 的顾客有 60% 的可能性会购买三种糖果中的一种。沃尔玛能用这样的信息做什么？沃尔玛的首席采购官李·斯科特 (Lee Scott) 说：“我一点头绪都没有。”你能做些什么来帮助沃尔玛增加业务？

关联分析

动机：发现数据中有趣或有用的模式、规律和趋势。例如：

哪些产品经常一起购买？
购买PC后会购买哪些产品？
哪些DNA对这种新型药物敏感？
如何自动对网络文档进行分类？
哪些博主和论坛用户可能具有反社会倾向？

关联规则挖掘

关联规则挖掘：搜索数据集中项目之间的关系。

在信息存储库中查找项目集或对象集之间的频繁模式、关联、相关性或因果结构。
频繁模式：数据库中频繁出现的模式（项目集、序列等）。

规则形式：\(X\rightarrow Y\)

基本概念

~~怎么又是集合论~~

令\(I=\{i_1,i_2,\cdots,i_d\}\)为数据集中的\(d\)个项目集，并且令\(T=\{t_1,t_2,\cdots,t_N\}\)为市场篮子数据中的\(N\)笔事务（交易）集合，其中\(N=\lvert T\rvert\)。每个\(t_j\)都是\(I\)的一个子集，包含从\(I\)中选择的一个或多个项目。

零个或多个项目的集合称为项目集。

如果一个项目集包含\(k\)个项目，则称为\(k\)项目集，例如：\(\{\text{bread},\text{coke},\text{milk}\}\)是一个\(3\)项目集。

空集（null，或空（empty））是不包含任何项目的项目集。

项目集\(Y\)是项目集\(X\)的超集（superset），或者等效地，如果\(X\)的所有项目也是\(Y\)的项目，则项目集\(X\)是项目集\(Y\)的子集。

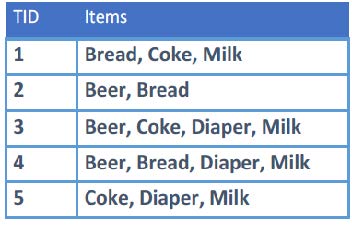
如果\(X\)是\(t_j\)的子集，即\(X\subset t_j\)，则称事务\(t_j\)包含项目集\(X\)。例如，\(X=\{\text{diaper},\text{milk}\}\)和\(X\subset t_4\)。

项目集的支持计数（support count）\(\sigma(X)\)是指包含项目集\(X\)的事务的数量。

支持度：\(\frac{\sigma(X)}{\lvert T\rvert}\)

关联规则是\(X\rightarrow Y\)形式的含义，其中\(X\subset I,Y\subset I\)，且\(X\cap Y=\emptyset\)。例如\(\{\text{diaper},\text{milk}\}\rightarrow\{\text{beer}\}\)

关联规则的强度可以通过其支持度（support）和置信度（confidence）来衡量。

支持度指定规则在给定数据集中的适用频率。
置信度指定\(Y\)中的项目在包含\(X\)的交易中出现的频率。

支持度与置信度

事务数据集\(T\)中关联规则\(X\rightarrow Y\)的支持度和置信度的正式定义：

\[\begin{aligned}\text{support}(X)&=\frac{\sigma(X)}{\lvert T\rvert}=P(X)\\\text{supoort}(X\rightarrow Y)&=\frac{\sigma(X\cup Y)}{\lvert T\rvert}=P(X\cup Y)\\\text{confidence}(X\rightarrow Y)&=\frac{\sigma(X\cup Y)}{\sigma(X)}=\frac{P(X\cup Y)}{P(X)}=P(Y\vert X)\end{aligned}\]

关联规则挖掘（Association Rule Mining，ARM）

关联规则挖掘：给定一组事务\(T\)，找到所有具有\(\text{support}\ge\text{minsup}\)和\(\text{confidence}\ge\text{minconf}\)的规则（\(X\rightarrow Y\)），其中\(\text{minsup}\)和\(\text{minconf}\)是相应的支持度和置信度阈值。

一种暴力方法是计算每条可能规则的支持度和置信度。然而，这种方法的计算成本很高，因为对于包含\(d\)个项目的数据集，总共有\(3^d-2^{d+1}+1\)条可能的规则。例如，当\(d=6\)时，有\(602\)种可能的规则

ARM中的两个任务

为了降低关联规则挖掘的计算复杂度，我们可以将问题分为两个子任务：

频繁项集生成：找出所有满足\(\text{minsup}\)阈值的项集，这些项集称为频繁项集。
规则生成：从频繁项集中提取所有高置信度的规则，这些规则称为强规则。

频繁项集生成的计算要求通常比规则生成的计算要求更高。

频繁项集生成

格结构（Lattice Structure，1. 格 Lattice）可用于枚举所有可能的项目集

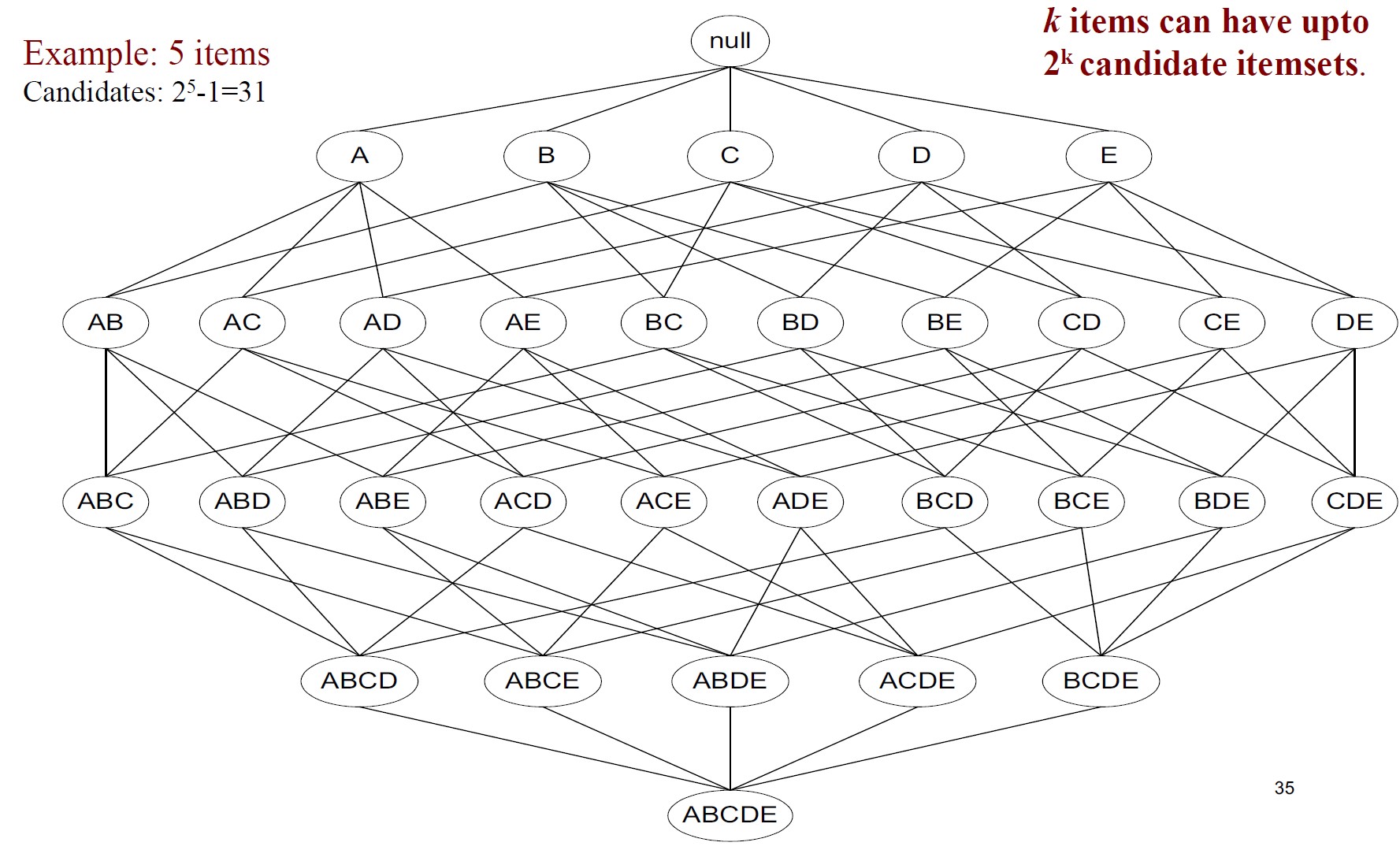
包含\(k\)个项目的数据集最多可以有\(2^k-1\)个可能的项目集。（组合数学：\(\sum_{i=0}^n{n\choose i}=2^n\)）

查找频繁项集的一种强力方法是确定格结构中每个候选项集的支持计数。

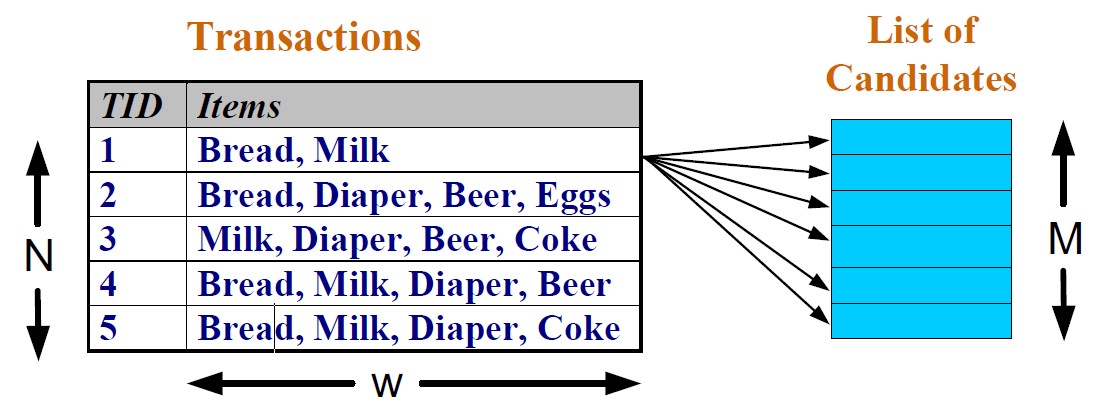
这种方法需要\(\mathrm O(NMw)\)次比较，其中\(N\)是事务数，\(M=2^k-1\)是候选项集数，\(w\)是最大事务宽度。

Apriori算法

Apriori原理

为了降低频繁项集生成的计算复杂度，我们可以

减少候选项目集的数量（\(M\)）。
减少比较次数

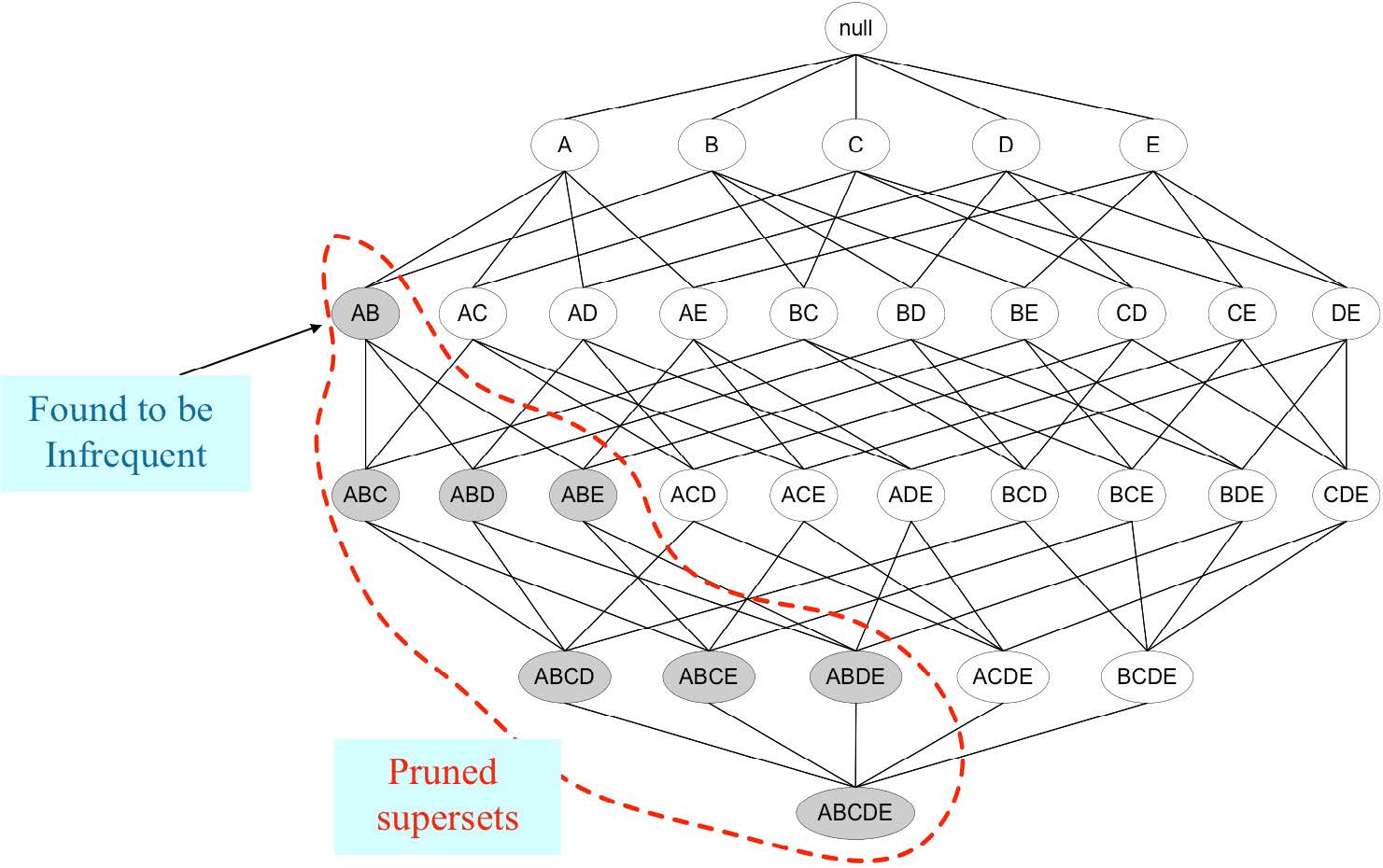
Apriori原理：如果一个项集是频繁的，那么它的所有子集也必须是频繁的。

可以使用Apriori原理来消除一些候选项集，而无需知道它们的支持度。可以通过使用更高级的数据结构来存储候选项集或压缩数据集来减少比较的次数。

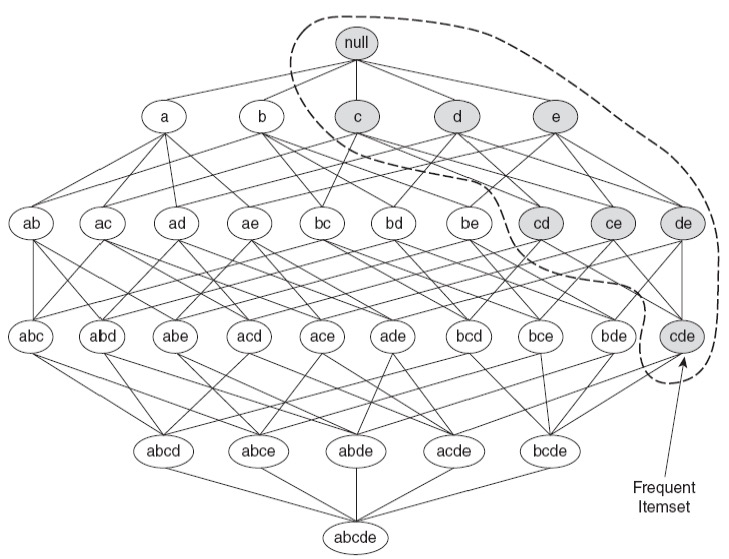
如果\{c,d,e\}是频繁项集，则其所有子集也必须是频繁的 — 如果\(\{c,d,e\}\)是频繁项集，则其所有子集也必须是频繁的

Apriori基于支持度\(\sigma\)的剪枝：

如果\{A,B\}是不频繁项集，那么它的所有超集都是不频繁的。此策略可用于减少候选项集的数量。 — 如果\(\{A,B\}\)是不频繁项集，那么它的所有超集都是不频繁的。此策略可用于减少候选项集的数量。

Apriori算法

令\(k=1\)
生成所有长度为\(1\)的频繁项集
重复以下步骤，直到不再识别出新的频繁项集：
1. 从频繁\(k\)项集生成候选\((k+1)\)项集
2. 修剪包含不频繁的\(k\)项集的候选\((k+1)\)项集
3. 通过扫描数据集，计算各个候选项集的支持度
4. 消除所有不频繁的候选项集

Apriori的原则

Apriori算法使用基于支持度的剪枝来控制候选项集的指数增长。
仅当前\(k-1\)个项目相同时，它才会通过合并一对频繁\(k\)项集来生成候选\((k+1)\)项集。
当生成每个候选\((k+1)\)项集时，会使用额外的候选剪枝步骤来确保候选的剩余\(k\)个子集是频繁的。否则，保证候选是不频繁的。

如何生成候选？

假设\(L_k\)中的项目按顺序列出

自连接\(L_k\)
插入到\(C_{k+1}\)
从\(L_{kp}\)和\(L_{kq}\)中选择\(\text{p.item}_1,\text{p.item}_2,\cdots,\text{p.item}_k,\text{q.item}_k\)
其中\(\text{p.item}_1=\text{q.item}_1,\cdots,\text{p.item}_{k-1}=\text{q.item}_{k-1},\text{p.item}_k\lt\text{q.item}_k\)

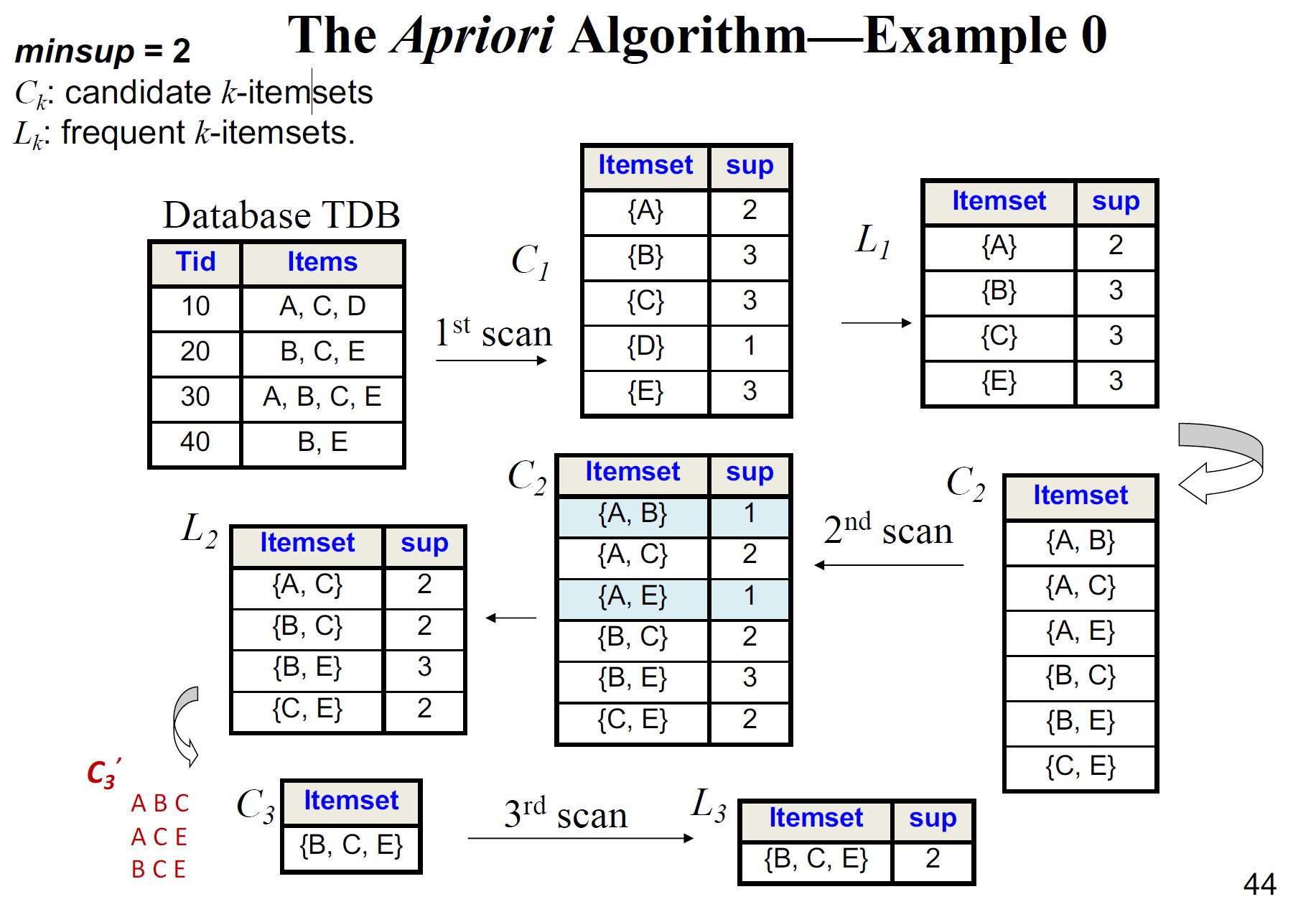
Apriori算法 - 示例

示例：通过合并频繁\(2\)项集对来生成和修剪候选\(3\)项集。

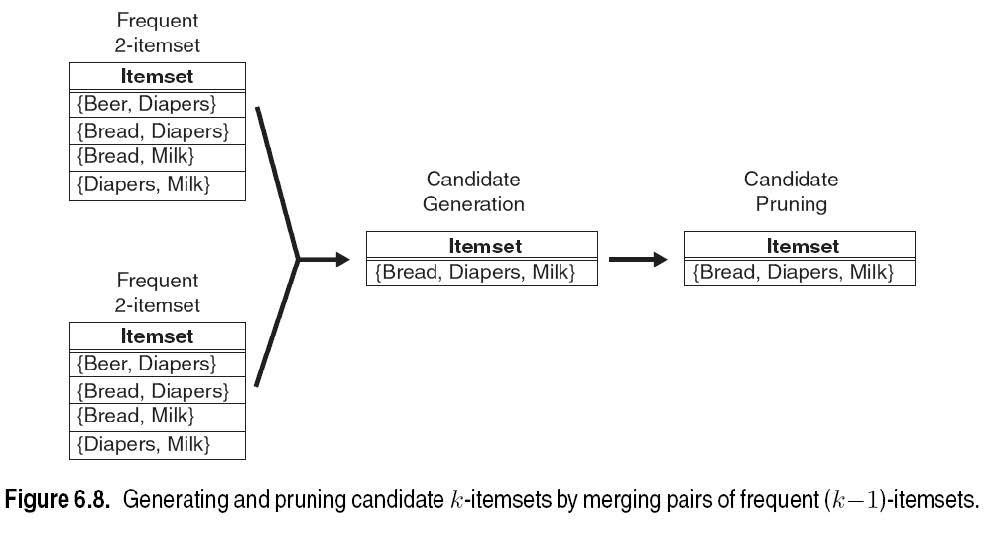
不需要将\(\{\text{beer},\text{diaper}\}\)与\(\{\text{bread},\text{milk}\}\)合并，因为它们的第一个项目不同。

如果\(\{\text{bread},\text{diaper},\text{milk}\}\)是可行的候选，那么可以通过合并\(\{\text{bread},\text{diaper}\}\)和\(\{\text{bread},\text{milk}\}\)来获得，但如果\(\{\text{bread},\text{milk}\}\)不是频繁的\(2\)项集？

FP-Tree和FP-Growth

FP-Growth（频繁模式增长）通过将频繁项目表示为FP-Tree（频繁模式树）来压缩数据集。

FP-tree的构建方式是每次读取数据集中的一个事务，并将每个事务映射到FP-Tree中的一条路径上，其中不频繁的项目被丢弃，频繁的项目按支持计数的降序排列。如果不同的事务有几个共同的项目，它们在FP树中的路径可能会重叠。（字典树）

一旦构建了FP-Tree，FP-Growth就会使用递归分治的方法来挖掘频繁项集。

FP-Growth算法

请看博客：数据挖掘随笔（二）FP-growth算法——一种用于频繁模式挖掘的模式增长方式(Python实现)

FP-Growth高效且可扩展，适用于挖掘长频繁项集和短频繁项集。它比Apriori算法快一个数量级。

FP-Growth算法的关键步骤：

构建FP-Tree来压缩表示数据集。
为头表中的每个项目构建条件模式库。
从每个条件模式库构建条件FP-Tree。
递归挖掘条件FP-Tree并增加目前获得的频繁项集。如果条件FP-Tree包含一条路径，则只需枚举所有项集即可。

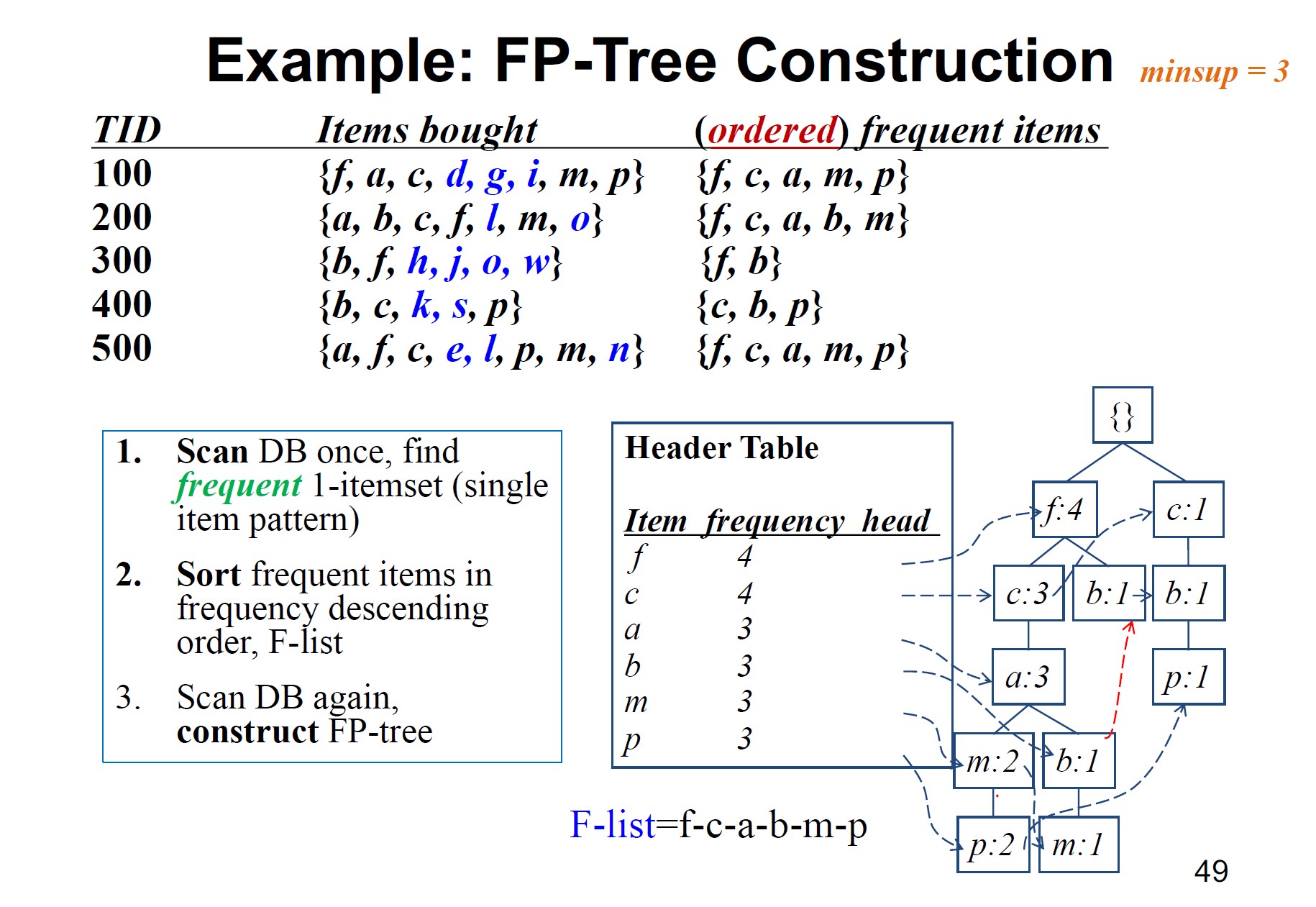
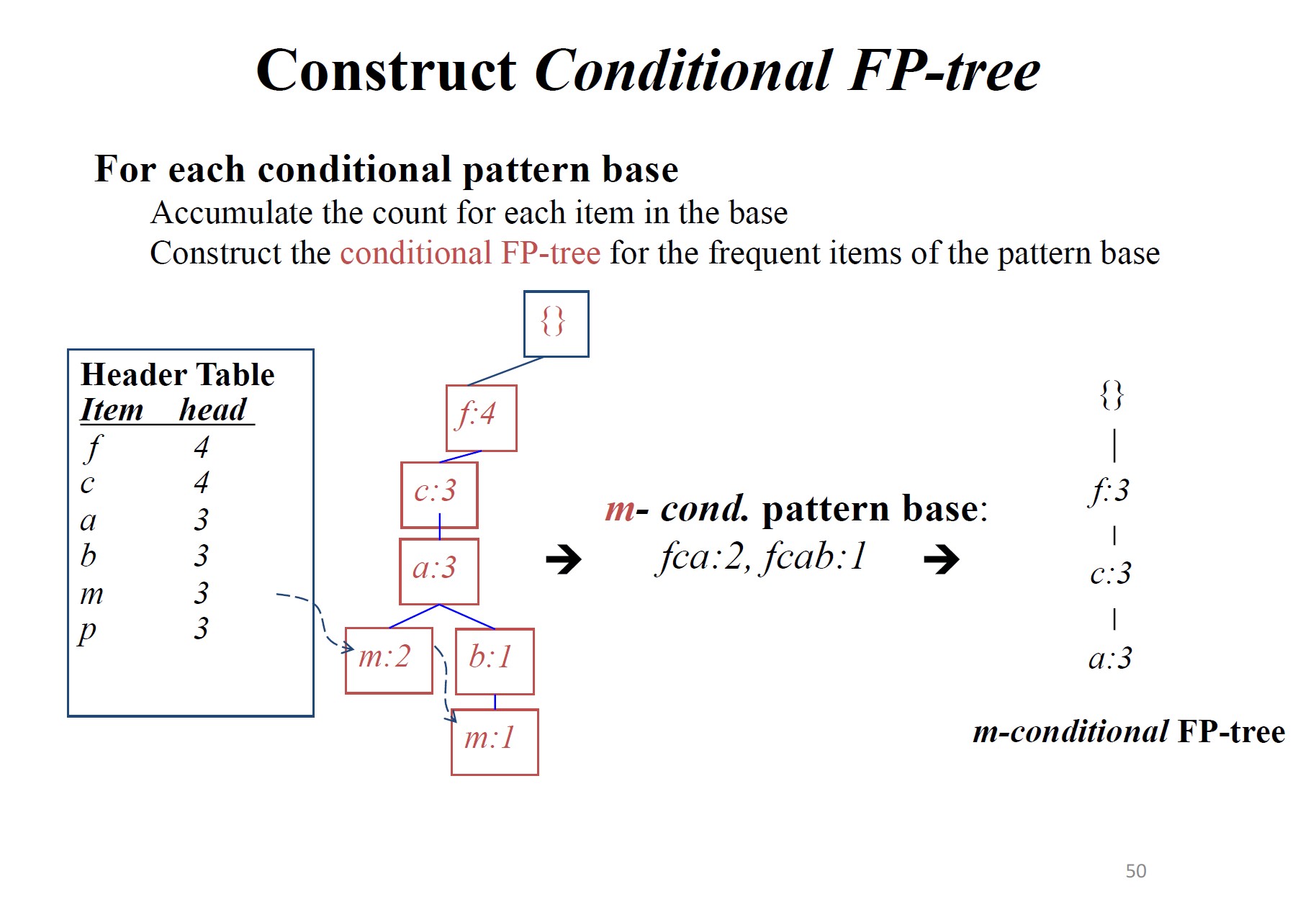
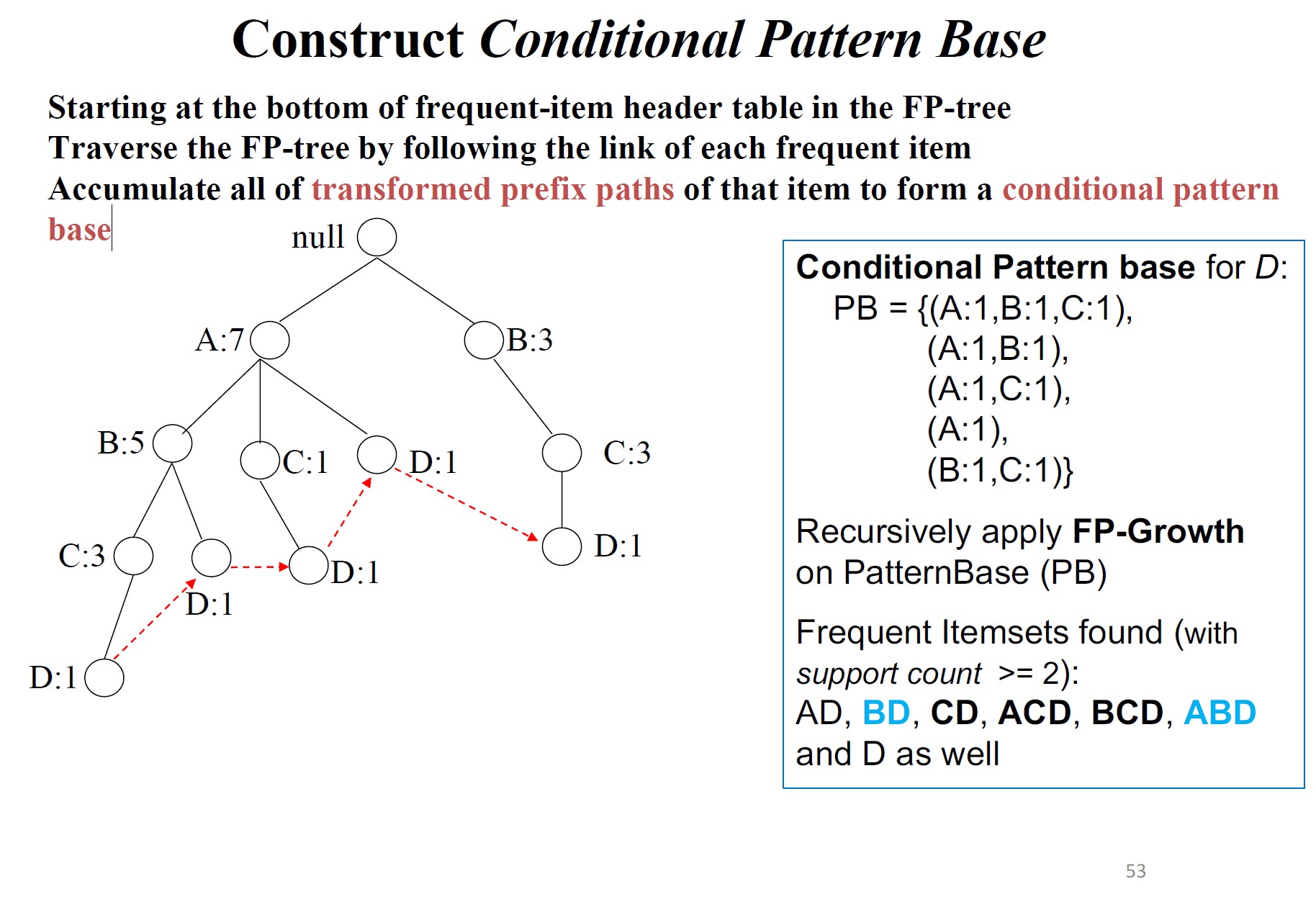
模式基：以该项为结尾的路径条数

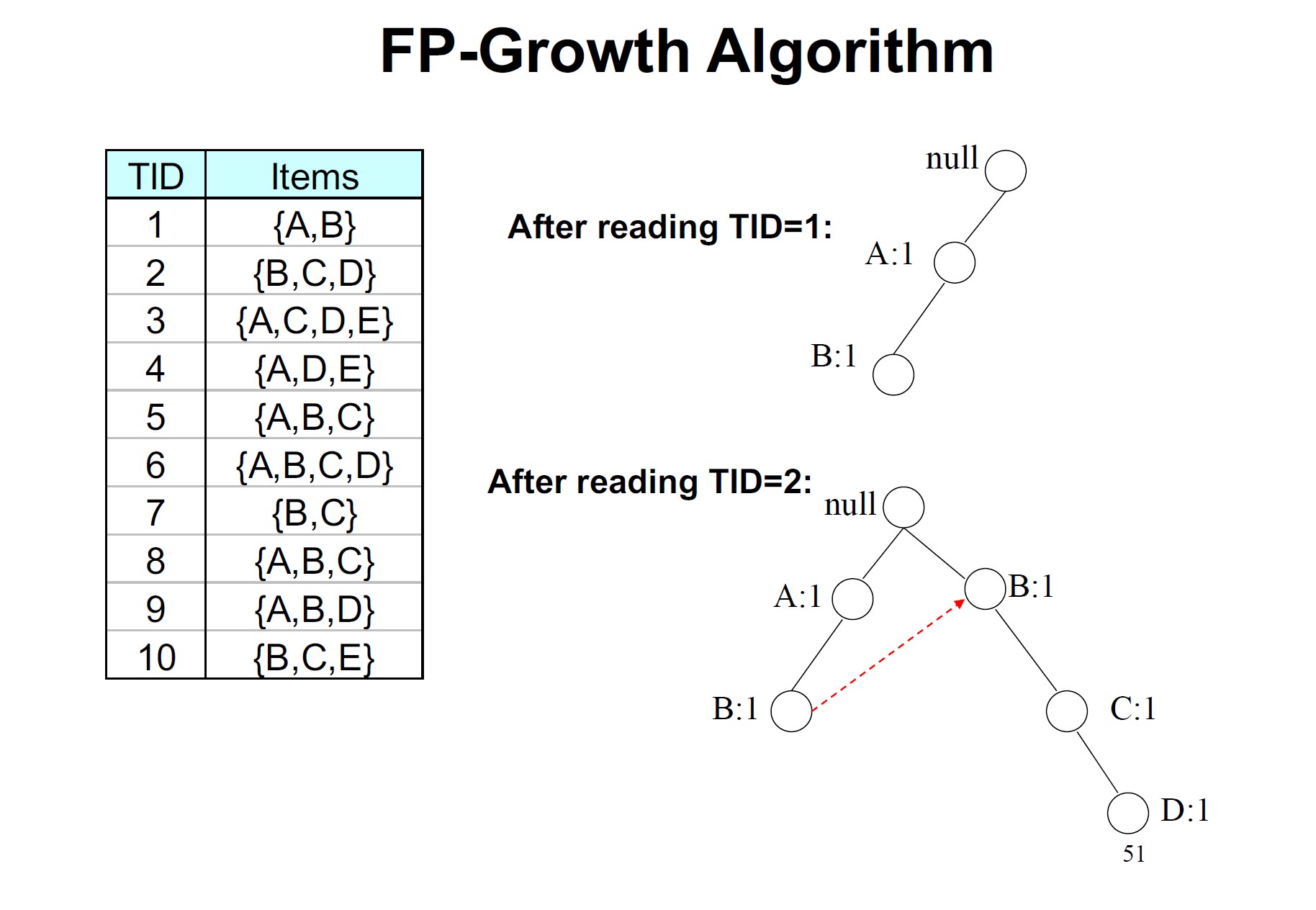
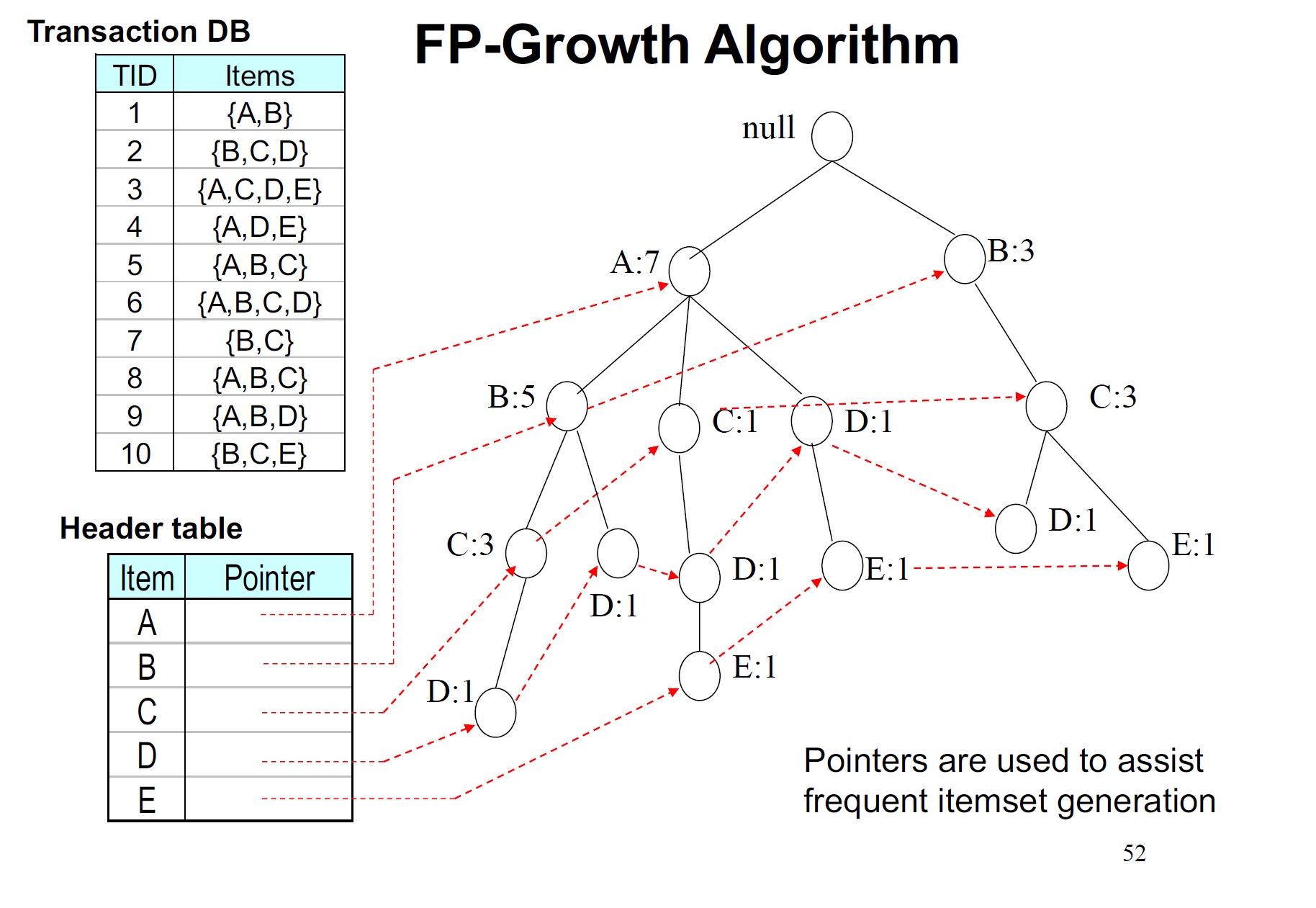
从FP-tree中频繁项头表的底部开始，通过跟踪每个频繁项的链接遍历FP-tree，累积该项目的所有转换前缀路径以形成条件模式库

FP-Growth的原理

模式增长性质：设\(\alpha\)为\(DB\)中的频繁项集，\(B\)为\(\alpha\)的条件模式基，\(\beta\)为\(B\)中的项集。若\(\beta\)在\(B\)中频繁出现，则\(\alpha\cup\beta\)为\(DB\)中的频繁项集。

FP-Growth结论

FP-tree：一种新颖的数据结构，存储有关频繁模式的压缩关键信息，对于频繁模式挖掘来说紧凑而完整。
FP-Growth：一种有效的大型数据库中频繁模式挖掘方法：使用高度紧凑的FP树，本质上是分治的方法。

练习

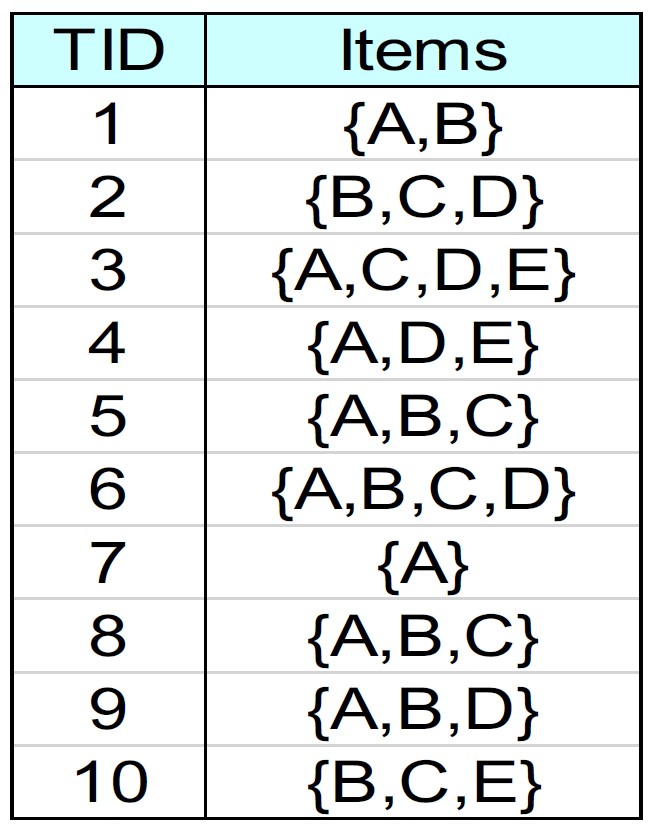
\(1)\)

使用FP-Growth算法从以下数据集中找出所有\(\text{minsup}=2\)的频繁项集。

#include <algorithm>
#include <iostream>
#include <vector>

/*
数据格式：
第一行三个正整数N，T，S，分别表示项目数、事务数和minsup，项目为1,2,...,N
接下来T行，每行第一个整数t为该事务的项目数，其后为t个项目
*/

int N, T;

std::vector<int> trans[10010];

int sp_cnt[10010];  // sp_cnt[0] == minsup
int idx[10010], rank[10010];

struct FPNode {
  int idx, cnt;
  FPNode** child;
  FPNode(const int& n = 0) {
    this->idx = this->cnt = 0;
    if (n) this->child = new FPNode*[n + 1];
    for (int i = 1; i <= n; ++i) this->child[i] = nullptr;
  }
};

void Build(FPNode* cur, std::vector<int>& nxt, const int& depth) {
  if (depth >= nxt.size()) return;
  if (cur->child[nxt[depth]] == nullptr) {
    cur->child[nxt[depth]] = new FPNode(N);
    cur->child[nxt[depth]]->idx = nxt[depth];
  }

  ++cur->child[nxt[depth]]->cnt;
  Build(cur->child[nxt[depth]], nxt, depth + 1);
}

typedef std::pair<std::vector<int>, int> pvi;
std::vector<pvi> base[10010];

void DFS(FPNode* cur, std::vector<int>& cur_base) {
  if (cur_base.size()) base[cur->idx].push_back(pvi(cur_base, cur->cnt));
  if (cur->idx) cur_base.push_back(cur->idx);
  for (int i = 1; i <= N; ++i) {
    if (cur->child[i] != nullptr) {
      DFS(cur->child[i], cur_base);
    }
  }
  if (cur->idx) cur_base.pop_back();
}

bool Contain(std::vector<int>& cur, const int& x) {
  for (auto i = cur.begin(); i != cur.end(); ++i) {
    if (*i == x) return true;
  }
  return false;
}

std::vector<std::vector<int>> FPSet[10010];

bool Equal(std::vector<int>& a, std::vector<int>& b) {
  if (a.size() != b.size()) return false;
  for (auto i = a.begin(), j = b.begin(); i != a.end(); ++i, ++j) {
    if (*i != *j) return false;
  }
  return true;
}

int mining_vis[10010];

void Plus(const int& maxx) {
  for (int i = 0; i < 1 << maxx; ++i) {
    if (mining_vis[i]) {
      mining_vis[i] = 0;
    } else {
      mining_vis[i] = 1;
      return;
    }
  }
}

std::vector<std::vector<int>> Mine(std::vector<int> x) {
  std::vector<std::vector<int>> ret;
  for (int i = 0, maxx = x.size(); i < 1 << maxx; ++i) mining_vis[i] = 0;
  for (int i = 1, maxx = x.size(); i < 1 << maxx; ++i) {
    Plus(maxx);
    std::vector<int> tmp;
    for (int j = 0; j < 1 << maxx; ++j) {
      if (mining_vis[j]) {
        tmp.push_back(x[j]);
      }
    }
    ret.push_back(tmp);
  }
  return ret;
}

int main(int argc, char** argv) {
  freopen("test.in", "r", stdin);

  std::cin >> N >> T >> sp_cnt[0];
  for (int i = 0, t; i < T; ++i) {
    std::cin >> t;
    for (int j = 0; j < t; ++j) {
      trans[i].push_back(0);
      std::cin >> trans[i][j];
      ++sp_cnt[trans[i][j]];
    }
  }

  // support count排序并*去掉*小于minsup的
  for (int i = 1; i <= N; ++i) idx[i] = i;
  std::sort(idx + 1, idx + N + 1,
            [](int a, int b) -> bool { return sp_cnt[a] > sp_cnt[b]; });
  for (int i = 1; i <= N; ++i) rank[idx[i]] = i;

  // 每一个事务排序，并且删除小于minsup的
  for (int i = 0; i < T; ++i) {
    std::sort(trans[i].begin(), trans[i].end(),
              [](int a, int b) -> bool { return rank[a] < rank[b]; });
    trans[i].erase(std::upper_bound(trans[i].begin(), trans[i].end(), 0,
                                    [](int a, int b) -> bool {
                                      return sp_cnt[a] > sp_cnt[b];
                                    }),
                   trans[i].end());
    trans[i].shrink_to_fit();
  }
  // 建立FP-Tree
  FPNode* root = new FPNode(N);
  for (int i = 0; i < T; ++i) Build(root, trans[i], 0);

  // DFS获取FP基
  std::vector<int> cur_base;
  DFS(root, cur_base);

  // 根据minsup进行裁剪FP基
  for (int i = 1; i <= N; ++i) {
    int trans_sp_cnt[10010] = {sp_cnt[0]};
    for (int j = 1; j <= N; ++j) trans_sp_cnt[j] = 0;
    for (int j = 0; j < base[i].size(); ++j) {
      for (int k = 0; k < base[i][j].first.size(); ++k) {
        trans_sp_cnt[base[i][j].first[k]] += base[i][j].second;
      }
    }
    int trans_idx[N + 1], trans_rank[N + 1];
    for (int j = 1; j <= N; ++j) trans_idx[j] = j;
    std::sort(trans_idx + 1, trans_idx + N + 1,
              [trans_sp_cnt](int a, int b) -> bool {
                return trans_sp_cnt[a] > trans_sp_cnt[b];
              });
    int cut_idx = std::upper_bound(trans_idx + 1, trans_idx + N + 1, 0,
                                   [trans_sp_cnt](int a, int b) -> bool {
                                     return trans_sp_cnt[a] > trans_sp_cnt[b];
                                   }) -
                  trans_idx;
    for (int j = cut_idx; trans_sp_cnt[trans_idx[j]] > 0; ++j) {
      for (int k = 0; k < base[i].size(); ++k) {
        if (Contain(base[i][k].first, trans_idx[j])) {
          base[i].erase(base[i].begin() + k--);
        }
      }
    }
  }

  // 对每个FP基进行挖掘
  for (int i = 1; i <= N; ++i) {
    for (auto j = base[i].begin(); j != base[i].end(); ++j) {
      std::sort(j->first.begin(), j->first.end());
      j->second = j->first.size();
    }
    std::sort(base[i].begin(), base[i].end(),
              [](pvi a, pvi b) -> bool { return a.second < b.second; });
    for (auto j = base[i].begin(); j != base[i].end(); ++j) {
      std::vector<std::vector<int>> all = Mine(j->first);
      for (auto x = all.begin(); x != all.end(); ++x) {
        bool flag = true;
        auto target = std::lower_bound(
            FPSet[i].begin(), FPSet[i].end(), *x,
            [](std::vector<int> a, std::vector<int> b) -> bool {
              return a.size() < b.size();
            });
        for (auto y = target; y != FPSet[i].end() && y->size() == x->size();
             ++y) {
          if (Equal(*x, *y)) {
            flag = false;
            break;
          }
        }
        if (flag) FPSet[i].insert(target, *x);
      }
    }
  }

  // 输出所有频繁项集
  freopen("test.out", "w", stdout);

  for (int i = 1; i <= N; ++i) {
    if (FPSet[i].size() == 0) continue;
    std::cout << i << ": ";
    for (int j = 0; j < FPSet[i].size(); ++j) {
      std::cout << '{';
      for (int k = 0; k < FPSet[i][j].size(); ++k) {
        std::cout << FPSet[i][j][k] << ", ";
      }
      std::cout << i << "}";
      if (j + 1 != FPSet[i].size()) std::cout << ", ";
    }
    std::cout << std::endl;
  }

  return 0;
}

运行结果是

B: {A, B}
C: {B, C}, {A, C}, {A, B, C}
D: {C, D}, {B, D}, {A, D}, {B, C, D}, {A, C, D}, {A, B, D}, {A, B, C, D}
E: {C, E}, {D, E}, {A, E}, {C, D, E}, {A, C, E}, {A, D, E}, {A, C, D, E}

\(2)\)

使用Apriori查找频繁项集。

Apriori用C++写起来史中史，告辞。

关联规则评估

关联规则生成

给定一个频繁项集\(Y\)，找到所有非空子集\(X\subset Y\)，使得\(X\rightarrow Y–X\)满足最低置信度要求。

如果\(\lvert Y\rvert=k\)，除去\(Y\rightarrow\emptyset\)和\(\emptyset\rightarrow Y\)，则有\(2^k–2\)条候选关联规则

关联规则生成 - 示例

给定频繁项目集：\(Y=\{\text{milk},\text{peanutbutter},\text{bread}\}\)；\(k=3\)

\(Y\)的所有非空子集：

\[\begin{aligned}X_1&=\{\text{milk}\}\\X_2&=\{\text{peanutbutter}\}\\X_3&=\{\text{bread}\}\\X_4&=\{\text{milk},\text{peanutbutter}\}\\X_5&=\{\text{milk},\text{bread}\}\\X_6&=\{\text{peanutbutter},\text{bread}\}\\\end{aligned}\]

\(k=3\)；共\(2^3-2=6\)条候选规则\(X_i\rightarrow Y-X_i\)：

\[\begin{aligned}\{\text{milk}\}&\rightarrow\{\text{peanutbutter},\text{bread}\}\\\{\text{peanutbutter}\}&\rightarrow\{\text{milk},\text{bread}\}\\\{\text{bread}\}&\rightarrow\{\text{milk},\text{peanutbutter}\}\\\{\text{peanutbutter},\text{bread}\}&\rightarrow\{\text{milk}\}\\\{\text{milk},\text{bread}\}&\rightarrow\{\text{peanutbutter}\}\\\{\text{milk},\text{peanutbutter}\}&\rightarrow\{\text{bread}\}\\\end{aligned}\]

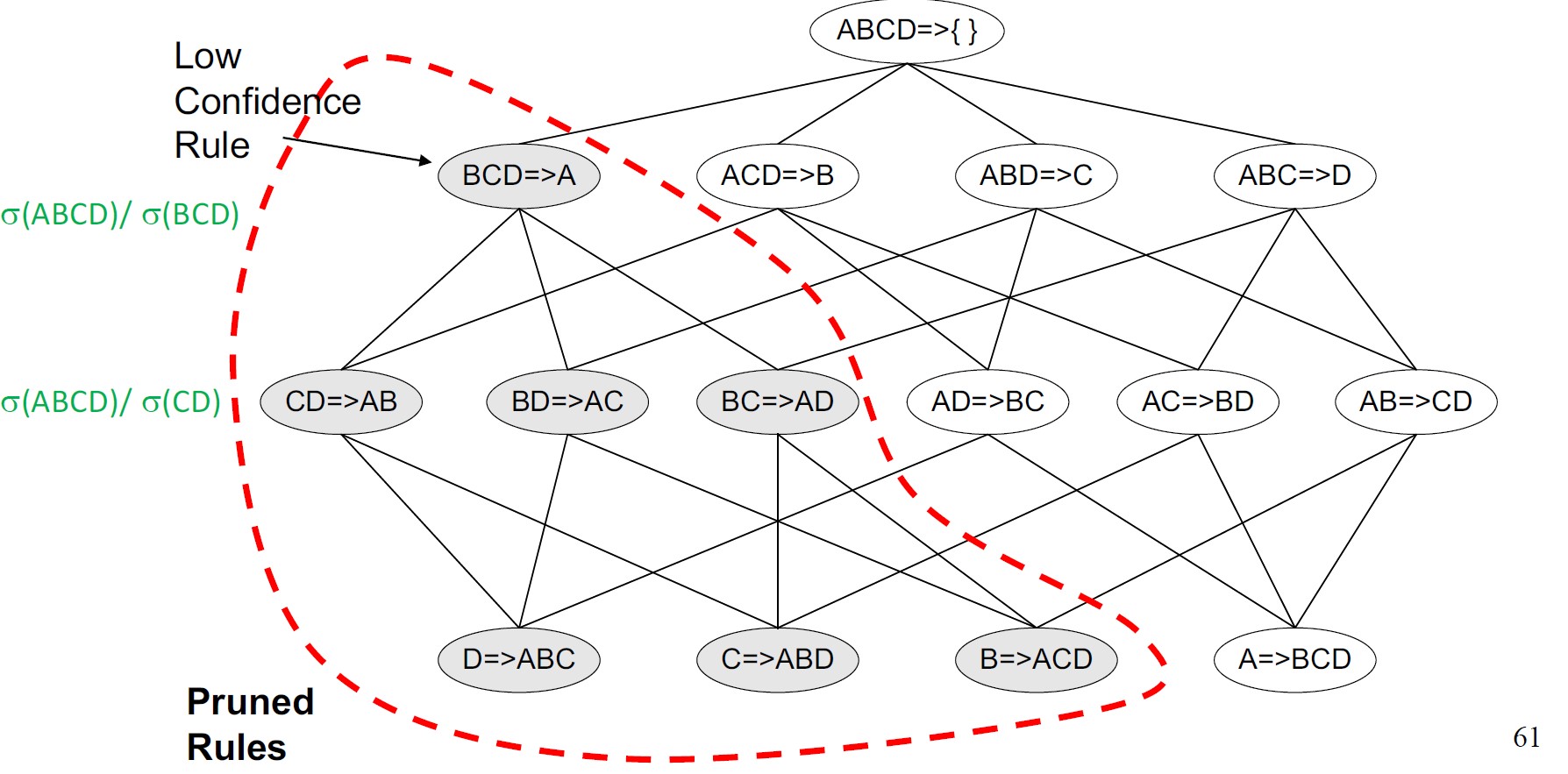
基于置信度的剪枝

基于置信度的剪枝：如果规则\(X\rightarrow Y-X\)不满足置信度阈值，则任何规则\(X'\rightarrow Y-X'\ ,X'\subset X\)也不能满足置信度阈值。

候选规则是通过合并规则结果中具有相同前缀的两个规则来生成的。

示例规则：

规则1：\(\{\text{diaper}\}\rightarrow\{\text{babywipe}\}\) [支持度=0.2，置信度=0.8]
规则2：\(\{\text{diaper}\}\rightarrow\{\text{milk}\}\) [支持度=0.15，置信度=0.3]

生成候选规则：在先行词中共享相同的前缀（左侧）：

候选规则：\(\{\text{diaper}\}\rightarrow\{\text{babywipe},\text{milk}\}\)

如果规则1或规则2不满足置信度阈值，则可以修剪该规则。

关联规则评估

关联分析可以潜在地生成大量的关联规则（模式）。其中一些强关联规则可能仍然不太有趣。

考虑以下喝茶和喝咖啡的人的例子：

尽管置信度\(P(\text{Coffee}\vert\text{Tea})\)很高，但该规则具有误导性，因为支持度\(P(\text{Coffee})\)和置信度\(P(\text{Coffee}\vert\overline{\text{Tea}})\)甚至更高。

提升度

为了解决这个问题，可以使用兴趣度度量来增强支持度-置信度度量，以识别有趣的关联规则。

提升度（Lift）是两个项目集\(X\)和\(Y\)之间的简单相关性度量，定义为

\[\text{lift}(X,Y)=\frac{\text{confidence}(X\rightarrow Y)}{\text{support}(Y)}=\frac{P(Y\vert X)}{P(Y)}=\frac{P(X\cup Y)}{P(X)P(Y)}\]

其中

\[\text{lift}(X,Y)\begin{cases}=1&,X\text{和}Y\text{相互独立}\\\gt1&,X\text{和}Y\text{正相关}\\\lt1&,X\text{和}Y\text{负相关}\end{cases}\]

对于所示的茶咖啡饮用者的例子，\(lift(\text{Tea},\text{Coffee})=0.9375\)，这表明茶饮用者和咖啡饮用者之间存在轻微的负相关性。

好多内容……