最大后验概率决策和分类器

如何在不确定的情况下做出最佳决策？我们来看一个简单的例子：

你完全看不清楚EEE学院教室里的一名学生。你需要决定/判断这名学生是男生还是女生。你的决定是什么？如果你不傻的话，你会根据EEE学院学生人数中\(70\%\)为男生、\(30\%\)为女生的事实判断这名学生是男生。假设会计学院的学生人数中男生占\(30\%\)，女生占\(70\%\)，那么在会计学院的教室里，您的决定是否相同？

您如何做出您的决策、描述您的决策规则或从科学、理论或数学的角度证明它是一个好的决策？

从数学上讲，这是基于我们的知识做出的最大概率决策，即对于EEE学院的男性和女性，\(p(\omega_1)=0.7\)和\(p(\omega_2)=0.3\)，对于会计学校的男性和女性，\(p(\omega_1)=0.3\)和\(p(\omega_2)=0.7\)。因此，明智的决策规则是，如果\(p(\omega_1)>p(\omega_2)\)，则判定\(\omega_1\)，反之亦然。

你的决定一定正确吗？不。但是还有其他更好的决定吗？没有。错误决定的概率（错误率）是\(p(\mathrm e)=0.3\)，这是最小值。

现在，如果您知道会计学院教室里的学生身高是\(1.75\)，您如何做出最佳决定？

没有区别。最佳决策仍基于\(p(\omega_1)\)和\(p(\omega_2)\)，看哪个更大。这么简单？是的！我们的世界里没有魔法。但现在\(p(\omega_i),\ i=1,2\)是什么？

就像会计学院的\(p(\omega_i)\)与EEE的\(p(\omega_i)\)不同一样，包含身高\(1.75\)的知识的\(p(\omega_i)\)与不包含此知识的\(p(\omega_i)\)也不同

为了方便起见，它们在数学上被表示为\(p(\omega_1\vert x)\)和\(p(\omega_2\vert x)\)，\(x=1.75\)，称为后验概率（aposterior probability）。它表示在特定场景下，在知道数据值\(x\)之后，类 \(\omega_i\)的概率。在不知道\(x\)值的情况下，\(p(\omega_1)\)和\(p(\omega_2)\)则改称为先验概率（prior probability）。

将决策规则的名称由最大概率决策修改为最大后验概率决策，简称MAP决策。因此，一般来说，我们有MAP决策规则：

决定\(\omega_k\)：如果\(p(\omega_k\vert x)\gt p(\omega_i\vert x),\ i\neq k\) 或者更一般地：\(\omega_k=\argmax_{\omega_i}\left[p(\omega_i\vert x)\right]\)

当你根据观测值\(x\)决定\(\omega_k\)时，你做出正确决定的概率为\(p(\omega_k\vert x)\)。因此，你做出错误决定的概率或错误率为：

\[p(\mathrm e_k\vert x)=1-p(\omega_k\vert x)\]

如果你的决策是\(\omega_k\)，因为\(p(\omega_k\vert x)\)最大，所以决策错误的概率最小。因此，该决策规则从最小化错误决策概率的意义上来说是最佳的。

最大后验（MAP）决策规则即最小化决策错误的概率。

\[\omega_k=\argmax_{\omega_i}\left[p(\omega_i\vert x)\right]=\argmin_{\omega_i}\left[p(\mathrm e_i\vert x)\right]\]

但是，获取\(p(\omega_i\vert x)\)的值并不十分简单，获取\(p(\omega_i)\)和\(p(x\vert\omega_i)\)的值则更为简单和方便，这两个值被称为类条件概率。

根据概率论的基本规则：

\[p(x,\omega_i)=p(x)p(\omega_i\vert x)=p(\omega_i)p(x\vert\omega_i)\]

我们有

\[p(\omega_i\vert x)=\frac{p(\omega_i)p(x\vert\omega_i)}{p(x)}\]

其中

\[p(x)=\sum_{i=1}^cp(\omega_i)p(x\vert\omega_i)\]

\(p(x)\)称为混合概率密度函数（PDF）或概率质量函数（PMF），即一个人的身高在\(x\)处的概率（密度）。我们可以将其从决策中移除，因为它在所有类别中都具有相同的值。

现在我们知道了如何在特定值\(x=1.75\ \mathrm m\)下做出最佳决策/识别，并计算错误率。这个概念很直观，很容易理解。

然而，要完全自动识别一个人在所有\(x\)值下的性别，我们需要\(x\)所有可能值的类条件概率\(p(x\vert\omega_i)\)。这带来了巨大的挑战。

是否有可能简化系统的计算？将决策转化为分类。如下图，我们以\(1.69\ \mathrm m\)为界限，高于该值，我们分类是男性，否则分类是女性。

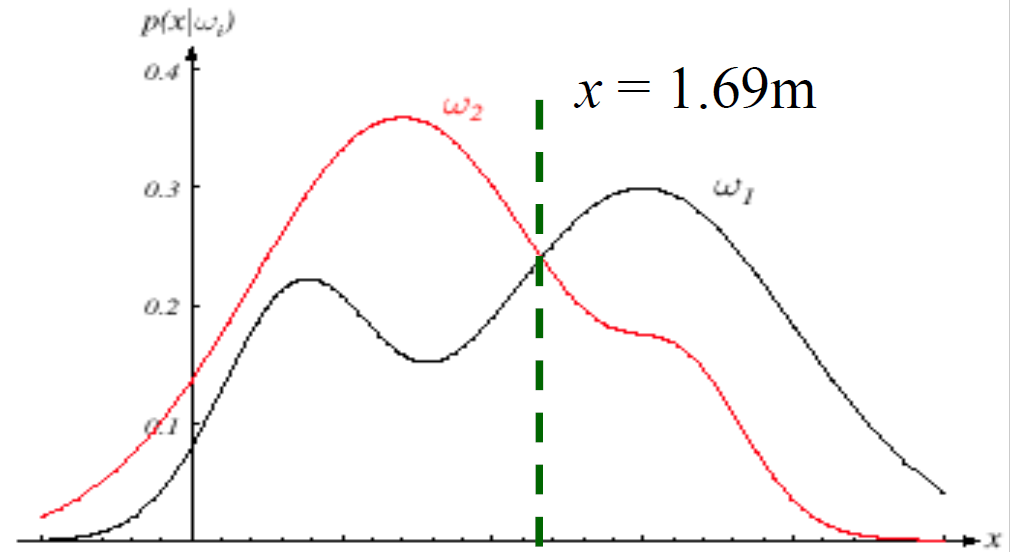
系统有多好？或者系统的性能如何？或者如何评价你设计的系统？

\[\text{决定}: \omega_k=\argmax_{\omega_i}[p(\omega_i\vert x)]\]

我们已经了解了计算特定\(x\)值的错误概率的公式。

\[p(\mathrm e_k\vert x)=1-p(\omega_k\vert x)=\sum_{i=1,i\neq k}^cp(\omega_i\vert x)\]

不难理解，识别系统的性能可以通过\(p(\mathrm e_k\vert x)\)对所有可能\(x\)值的平均值来衡量。

如何对\(x\)的所有可能值求\(p(\mathrm e_k\vert x)\)的平均值？

对离散\(x\)：

\[p(\mathrm e)=\sum_{x=-\infty}^{+\infty}p(\mathrm e_k\vert x)p(x)\]

对连续\(x\)：

\[p(\mathrm e)=\int_{-\infty}^{+\infty}p(\mathrm e_k\vert x)p(x)\mathrm dx\]

又

\[\begin{aligned}p(\mathrm e)&=\int_{-\infty}^{+\infty}p(\mathrm e_k\vert x)p(x)\mathrm dx\\&=\int_{-\infty}^{+\infty}[1-p(\omega_k\vert x)]p(x)\mathrm dx\\&=\int_{-\infty}^{+\infty}[1-\frac{p(\omega_k)p(x\vert\omega_k)}{p(x)}]p(x)\mathrm dx\\&=1-\int_{-\infty}^{+\infty}p(\omega_k)p(x\vert\omega_k)\mathrm dx\end{aligned}\]

注意，对于\(x\)的不同区域，模式识别系统具有不同的决策\(\omega_k\)。决策/分类是将\(x\)的整个空间划分为\(c\)个决策区域\(\mathfrak R_i\)。因此，

\[\begin{aligned}p(\mathrm e)&=1-\sum_{i=1}^c\int_{\mathfrak R_i}p(\omega_i)p(x\vert\omega_i)\mathrm dx\\&=1-\sum_{i=1}^cp(\omega_i)\int_{\mathfrak R_i}p(x\vert\omega_i)\mathrm dx\end{aligned}\]

显然，正确决策的概率是

\[p(\text{correct})=1-p(\mathrm e)=\sum_{i=1}^cp(\omega_i)\int_{\mathfrak R_i}p(x\vert\omega_i)\mathrm dx\]

对于二分类问题：

\[\begin{aligned}p(\mathrm e)&=1-p(\omega_1)\int_{\mathfrak R_1}p(x\vert\omega_1)\mathrm dx-p(\omega_2)\int_{\mathfrak R_2}p(x\vert\omega_2)\mathrm dx\\&=p(\omega_1)\int_{\mathfrak R_2}p(x\vert\omega_1)\mathrm dx+p(\omega_2)\int_{\mathfrak R_1}p(x\vert\omega_2)\mathrm dx\end{aligned}\]

现在，如果我们不仅知道人的身高\(x_1\)，还知道头发的长度\(x_2\)，那么不难想象我们会做出更好的决定，即错误概率更低。只要现在使用向量\(\mathbf x=[x_1,x_2]^\intercal\)替换之前的标量\(x\)，识别原理将与以前相同。概率分布现在是二维的。在1D情况下用于区分两个类别的标量阈值变成了\(x\)所跨平面上的曲线。

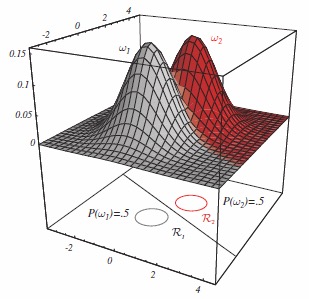
信息、数据或特征维度的增加一般都会增加正确决策的概率或降低决策错误的概率。

我们知道，最佳分类会最大化后验概率，从而最小化分类误差：

\[\text{决定}: \omega_k=\argmax_{\omega_i}[p(\omega_i\vert\mathbf x)]=\argmin_{\omega_i}[p(\mathrm e_i\vert\mathbf x)]\]

因为：\(p(\omega_i\vert\mathbf x)=\frac{p(\omega_i)p(\mathbf x\vert\omega_i)}{p(\mathbf x)}\)，并且\(p(\mathbf x)\)不是\(\omega_i\)的函数，贝叶斯（最优）分类就是评估所谓的判别函数（discriminant functions），可以定义为\(g_i(\mathbf x)=\ln p(\mathbf x\vert\omega_i)+\ln p(\omega_i)\)，并找到对于给定模式\(\mathbf x\)具有判别函数最大值的类\(\omega_i\)。

这里应用了自然对数\(\ln\)，因为它是一个单调递增函数，不会影响决策结果，但如果\(p(\mathbf x\vert\omega_i)\)是指数函数，则会简化其评估。

我们将针对类条件PDF为多元高斯分布\(p(\mathbf x\vert\omega_i)=\mathrm N(\mu_i,\Sigma_i)\)的情况推导分类器

\[p(\mathbf x\vert\omega_i)=\frac1{(2\pi)^{\frac d2}\lvert\Sigma_i\rvert^{\frac12}}\exp\left[-\frac12(\mathbf x-\mu_i)^\intercal\Sigma_i^{-1}(\mathbf x-\mu_i)\right]\]

判别函数变成\(\mathbf x\)的二次函数：

\[\begin{aligned}g_i(\mathrm x)&=-\frac12(\mathbf x-\mu_i)^\intercal\Sigma_i^{-1}(\mathbf x-\mu_i)+\ln p(\omega_i)-\frac12\ln\lvert\Sigma_i\rvert-\frac d2\ln2\pi\\&=-\frac12(\mathbf x-\mu_i)^\intercal\Sigma_i^{-1}(\mathbf x-\mu_i)+b_i\\&=-\frac12d_{\Sigma_i}(\mathbf x,\mu_i)+b_i\end{aligned}\]

其中

\[\begin{aligned}d_{\Sigma_i}(\mathbf x,\mu_i)&=(\mathbf x-\mu_i)^\intercal\Sigma_i^{-1}(\mathbf x-\mu_i)\\b_i&=\ln p(\omega_i)-\frac12\ln\lvert\Sigma_i\rvert\end{aligned}\]

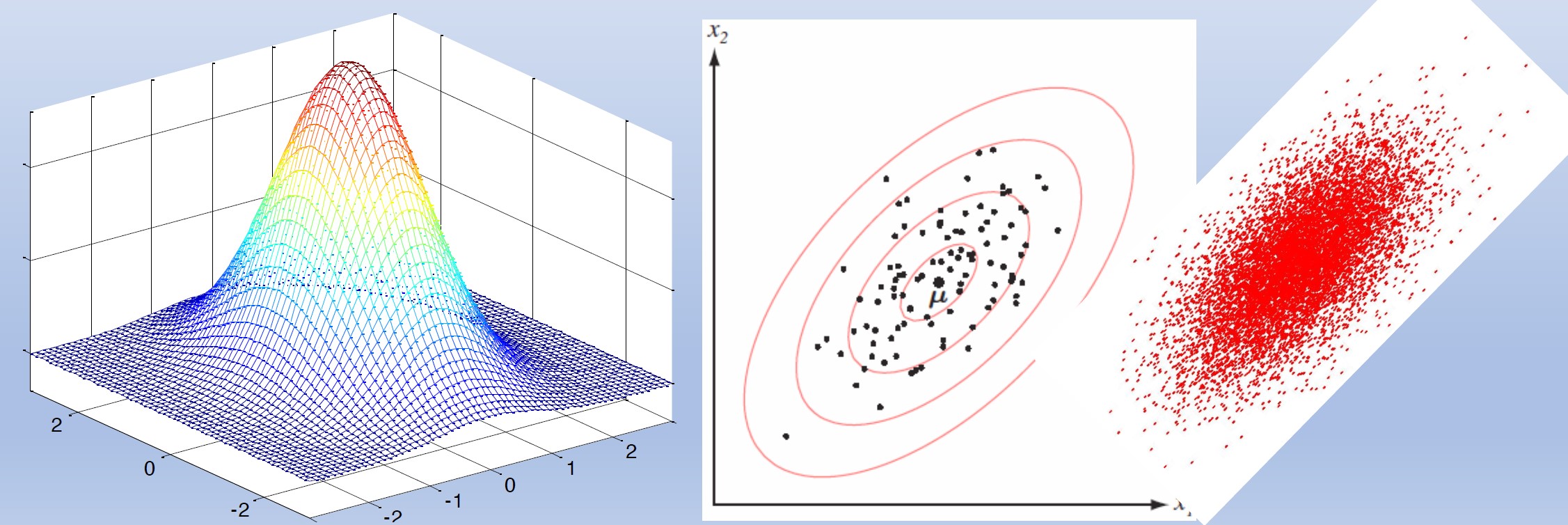
\(d_{\Sigma_i}(\mathbf x,\mu_i)\)称为\(\mathbf x\)和\(\mu_i\)之间的Mahalanobis距离的平方。

与欧氏距离的平方进行比较

\[d_{\text{Eu}}=(\mathbf x-\mu_i)^\intercal(\mathbf x-\mu_i)\]

一维的情况：

\[\begin{aligned}d_{\text{Eu}}(x,\mu_i)&=(x-\mu_i)^2\\d_\Sigma(x,\mu_i)&=\frac{(x-\mu_i)^2}{\sigma^2}\end{aligned}\]

（就是正态分布里面\(\exp\)的一坨东西）

对于二维高斯PDF从二维高斯中抽取的样本位于以均值为中心的云中。椭圆显示高斯的等概率密度线。椭圆上的所有点都具有相同的Mahalanobis距离，但与均值的欧几里得距离不同

二次分类器：回想一下，\(p(\mathbf x\vert\omega_i)=\mathrm N(\mu_i,\Sigma_i)\)的多元高斯类条件PDF的判别函数是

\[g_i(\mathrm x)=-\frac12(\mathbf x-\mu_i)^\intercal\Sigma_i^{-1}(\mathbf x-\mu_i)+\ln p(\omega_i)-\frac12\ln\lvert\Sigma_i\rvert\]

这是一般多元正态情况，其中每个类别的协方差矩阵不同。唯一可以删除的项是\(\frac d2\ln2\pi\)项（常数），并且得到的判别函数本质上是二次的：

\[g_i(\mathbf x)=\mathbf x^\intercal\mathbf W_i\mathbf x+\mathbf w_i^\intercal\mathbf x+\omega_{0i}\]

其中

\[\begin{aligned}\mathbf W_i&=-\frac12\Sigma_i^{-1}\\\mathbf w_i&=\Sigma_i^{-1}\mu_i\\\omega_{0i}&=-\frac12\mu_i^\intercal\Sigma_i^{-1}\mu_i+\ln p(\omega_i)-\frac12\ln\lvert\Sigma_i\rvert\end{aligned}\]

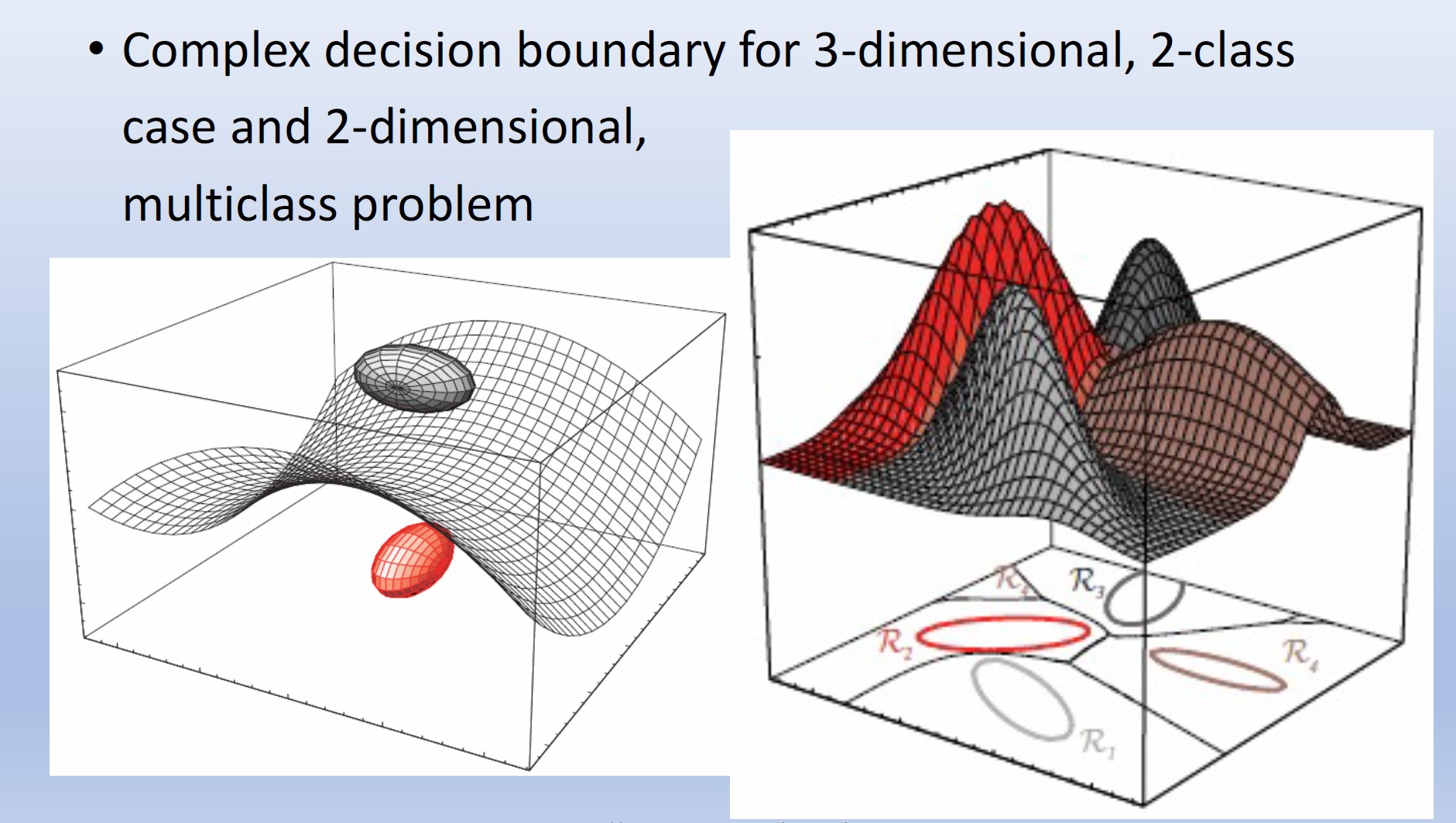
决策曲面是超二次曲面，可以采用任何一般形式的超平面、超平面对、超球面、超椭圆体、超抛物面以及各种类型的超双曲面

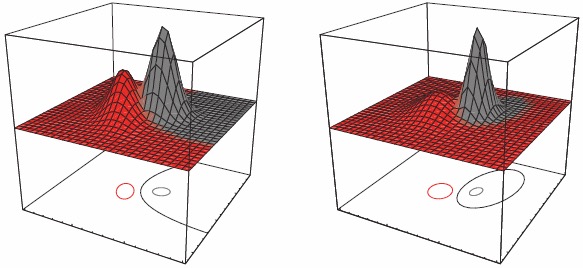
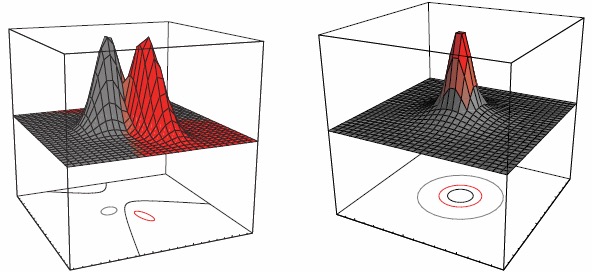
特殊情况1：所有类都拥有相同的协方差矩阵\(\Sigma_i=\Sigma\)。

判别函数简化为

\[\begin{aligned}g_i(\mathrm x)&=-\frac12(\mathbf x-\mu_i)^\intercal\Sigma_i^{-1}(\mathbf x-\mu_i)+\ln p(\omega_i)\\&=-\frac12\mathbf x^\intercal\Sigma_i^{-1}\mathbf x+\mu_i^\intercal\Sigma_i^{-1}\mathbf x-\frac12\mu_i^\intercal\Sigma_i^{-1}\mu_i+\ln p(\omega_i)\end{aligned}\]

并删除与类标签\(i\)无关的项，我们有

\[\begin{aligned}g_i(\mathrm x)&=\mu_i^\intercal\Sigma_i^{-1}\mathbf x-\frac12\mu_i^\intercal\Sigma_i^{-1}\mu_i+\ln p(\omega_i)\\&=\mathbf w_i^\intercal\mathbf x+\mathrm w_{i0}\end{aligned}\]

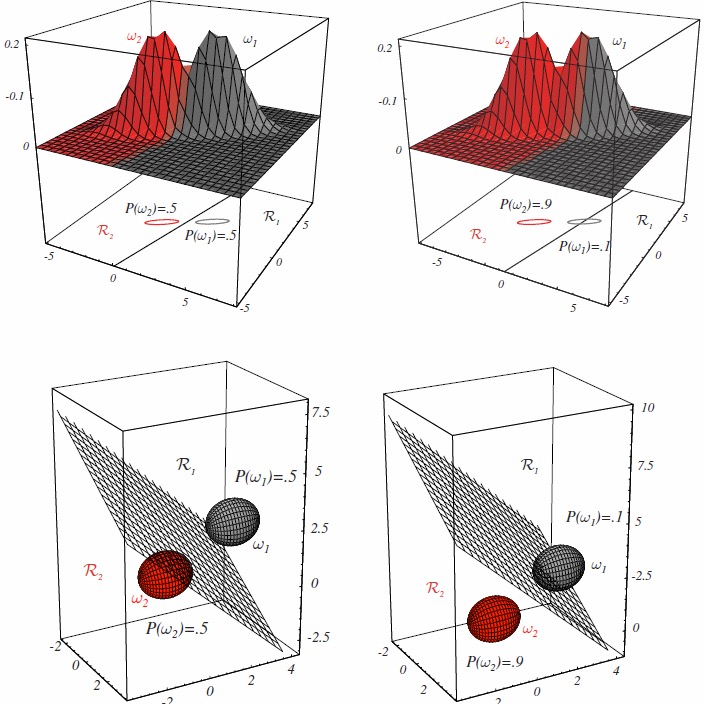
判别函数是\(\mathbf x\)的线性函数。这将产生一个线性分类器，因为我们将表明任何两个类之间的决策或分类边界是一个超平面。我们将\(\mathrm w_{i0}\)称为\(\omega_i\)类的阈值或偏差。

任何两个类别之间的决策或分类边界是方程的解。

\[ \begin{aligned} g_i(\mathbf x)&=g_j(\mathbf x)\\ (\mathbf w_i-\mathbf w_j)^\intercal\mathbf x+\mathrm w_{i0}-\mathrm w_{j0}&=0\\ (\mu_i-\mu_j)^\intercal\Sigma^{-1}\mathbf x-\frac12(\mu_i-\mu_j)^\intercal\Sigma^{-1}(\mu_i-\mu_j)+\ln\frac{p(\omega_i)}{p(\omega_j)}&=0 \end{aligned} \]

在二维空间\(\mathbf x\)中它是一条直线，在三维空间\(\mathbf x\)中它是一个平面，在高维空间\(\mathbf x\)中它是一个超平面。

我们看到，分隔两个类的决策超平面通常不与均值之间的线正交。（在什么情况下它是正交的？）

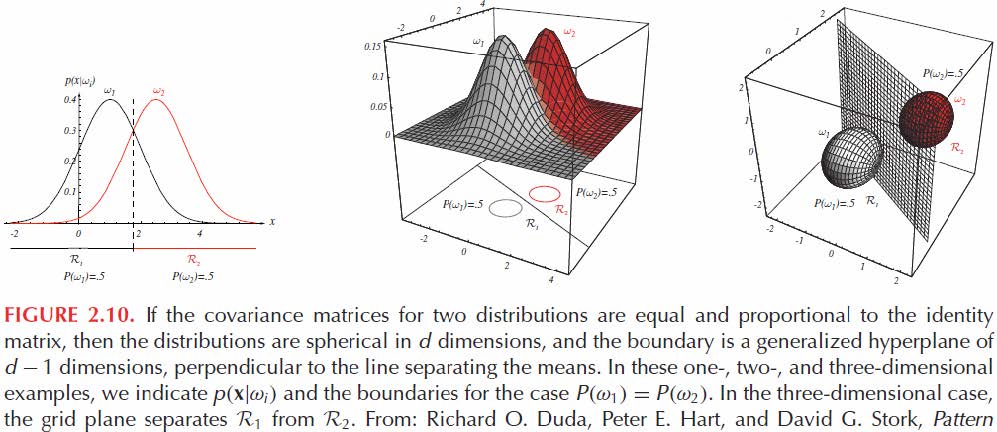
特殊情况2：所有类都具有相同的对角线标量协方差矩阵\(\Sigma_i=\sigma^2\mathbf I\)。\(\mathbf I\)是单位矩阵。

当所有特征（\(x\)的组成部分）在统计上不相关且每个特征具有相同的方差\(\sigma_2\)时，就会出现这种情况。

注意\(\Sigma_i=\sigma^2\mathbf I\Rightarrow\Sigma_i^{-1}=\frac{\mathbf I}{\sigma^2},\qquad\lvert\Sigma_i\rvert=\sigma^{2d}\)

判别函数简化为

\[\begin{aligned}g_i(\mathrm x)&=-\frac12(\mathbf x-\mu_i)^\intercal\Sigma_i^{-1}(\mathbf x-\mu_i)+\ln p(\omega_i)\\&=-\frac1{2\sigma^2}(\mathbf x-\mu_i)^\intercal(\mathbf x-\mu_i)+\ln p(\omega_i)\\&=-\frac1{2\sigma^2}(\mathbf x^\intercal\mathbf x-2\mu_i^\intercal\mathbf x+\mu_i^\intercal\mu_i)+\ln p(\omega_i)\end{aligned}\]

二次项\(\mathbf x^\intercal\mathbf x\)对于所有\(i\)类都是相同的，因此可以删除。乘以常数\(\sigma^2\)，判别函数简化为

\[\begin{aligned}g_i(\mathrm x)&=-2\mu_i^\intercal\mathbf x+\mu_i^\intercal\mu_i+\sigma^2\ln p(\omega_i)\\&=\mathbf w_i^\intercal\mathbf x+\mathrm w_{i0}\end{aligned}\]

我们将\(\mathrm w_{i0}\)称为\(\omega_i\)类的阈值或偏差。它是\(\mathbf x\)的线性函数。这产生了一个线性分类器。

任何两个类别之间的决策或分类边界是方程的解。

\[ \begin{aligned} g_i(\mathbf x)&=g_j(\mathbf x)\\ (\mathbf w_i-\mathbf w_j)^\intercal\mathbf x+\mathrm w_{i0}-\mathrm w_{j0}&=0\\ (\mu_i-\mu_j)^\intercal\mathbf x-\frac{\mu_i^\intercal\mu_i-\mu_j^\intercal\mu_j}2+\ln\frac{p(\omega_i)}{p(\omega_j)}&=0 \end{aligned} \]

该方程定义了一个与连接两个均值的线正交的超平面

回想一下判别函数

\[g_i(\mathrm x)=-\frac1{2\sigma^2}(\mathbf x-\mu_i)^\intercal(\mathbf x-\mu_i)+\ln p(\omega_i)\]

如果所有类别的先验概率相同，则

\[g_i(\mathrm x)=(\mathbf x-\mu_i)^\intercal(\mathbf x-\mu_i)=-d_{\text{Eu}}=\lVert\mathbf x-\mu_i\rVert\]

当这种情况发生时，最佳决策规则可以非常简单地表述为：对特征向量\(\mathbf x\)进行分类，测量\(\mathbf x\)到每个\(c\)个均值向量的欧几里得距离，并将\(\mathbf x\)分配给最接近均值的类别。这样的分类器称为最小距离分类器。如果将每个均值向量视为其类别中模式的理想原型或模板，那么这本质上就是一个模板匹配过程。