统计估计和机器学习
估计概率分布密度的非参数方法
我们知道最佳决策或最佳分类是:
\[\begin{aligned} \text{Decide}\ \omega_k&=\argmin_{\omega_i}[p(\mathrm e_i\vert\mathbf x)]=\argmin_{\omega_i}[1-p(\omega_i\vert\mathbf x)]\\ &=\argmax_{\omega_i}[p(\omega_i\vert\mathbf x)]=\argmax_{\omega_i}[p(\omega_i)p(\mathbf x\vert\omega_i)] \end{aligned}\]
要设计一个自动模式识别系统,我们需要知道\(\mathbf x\)所有值的概率分布/密度函数(PDF),以便系统能够对接收到的数据\(\mathbf x\)的任何值做出决策。在实践中,PDF通常是未知的,只能通过收集的示例/样本\(\{\mathbf x_i\}=[\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n]\)来估计,以便设计模式识别系统。
根据一组训练样本\(D=\{\mathbf x_i\}\)对随机变量\(\mathbf x\)确定一些规则或者一些确定性值是统计估计或者机器学习的任务。
概率分布/密度函数(PDF)是关于随机变量的完整信息。
直接估计后验概率\(p(\omega_k\vert\mathbf x)\)函数比较困难,因此我们学习先验概率\(p(\omega_k)\)和类条件概率函数\(p(\mathbf x\vert\omega_k)\)。
\(c\)先验概率可以通过以下方式轻松估计:
\[\hat p(\omega_k)=\frac{n_k}n\]
其中,\(n_k\)和\(n\)分别是\(\omega_k\)类的训练样本数和总训练样本数。
由于所有类别的估计方法相同,我们将\(p(\mathbf x\vert\omega_k)\)的符号简化为\(p(\mathbf x)\),并假设我们有\(n\)个样本\(\{\mathbf x_i\}=[\mathbf x_1,\mathbf x_2,\cdots,\mathbf x_n]\),根据概率定律\(p(\mathbf x)\)独立同分布(independently and identically distributed,i.i.d.,一组随机变量之间相互独立,并且具有相同的概率分布)。
根据概率密度函数的定义,\(\mathbf x\)落在区域\(R\)中的概率\(P\)为:
\[P(\mathbf x)=\int_{R_{\mathbf x}}p(\mathbf t)\mathrm d\mathbf t\approx p(\mathbf x)V\]
其中\(V\)是区域\(R_{\mathbf x}\)的体积。
如果在该类的\(n\)个训练样本中,有\(k\)个样本落在区域\(R\)中,则\(P\)的估计值为\(\hat P(\mathbf x)=\frac kn\)。因此,PDF \(p(\mathbf x)\)的估计值为
\[\hat P(\mathbf x)=\frac k{nV}\]
这被称为非参数方法来估计概率密度函数,因为没有应用任何模型假设。
Parzen窗口方法
基于\(n\)个训练样本估计PDF的过程是:给定\(\mathbf x\)的值,选择一个以\(\mathbf x\)为中心、大小(体积)为\(V\)的区域/单元,计算该区域/单元中的样本数\(k\)。然后估计\(\mathbf x\)处的概率密度\(p(\mathbf x)\)为:\(\hat p(\mathbf x)=\frac k{nV}\)
显然,区域/单元的形状和大小不同会导致PDF的估计值不同。
一般来说,\(\mathbf x\)是多维的\(\mathbf x=[x_1,x_2,\cdots,x_d]\)。如果我们选择一个边长为\(h\)的\(d\)维超立方体作为区域,样本\(\mathbf x_i=[x_{i1},x_{i2},\cdots,x_{id}]\)将落入超立方体,如果
\[\frac{\lvert x_j-x_{ij}\rvert}{h}\lt\frac12\ \text{for}\ \forall\ j=1,2,\cdots,d\]
因此,我们可以用数学方式将落入单元格\(k\)的样本数量表示为
\[k=\sum_{i=1}^nK\left(\frac{\mathbf x-\mathbf x_i}h\right)\]
其中Parzen窗口核函数定义为
\[ K=\begin{cases} 1&,\forall\ j=1,2,\cdots,d\quad\lvert u_j\rvert\lt\frac12\\ 0&,\text{Otherwise} \end{cases} \]
然后估计\(\mathbf x\)处的概率密度\(p(\mathbf x)\)为:
\[\hat p(\mathbf x)=\frac1{nh^d}\sum_{i=1}^nK\left(\frac{\mathbf x-\mathbf x_i}h\right)\]

由于矩形核函数不光滑,因此矩形核函数产生的PDF不光滑。实际上,我们可以选择任何函数作为核,只要满足:
\[ \begin{aligned} K(\mathbf u)&\geq0\\ \int_{-\infty}^{+\infty}K(\mathbf u)\mathrm d\mathbf u&=\int_{-\infty}^{+\infty}K\left(\frac{\mathbf x-\mathbf x_i}h\right)\mathrm d\frac{\mathbf x-\mathbf x_i}h=\int_{-\infty}^{+\infty}\frac1{h^d}K\left(\frac{\mathbf x-\mathbf x_i}h\right)\mathrm d\mathbf x=1 \end{aligned} \]
因此,任意PDF函数都可以作为核函数,这种方法称为Parzen窗口方法,实际上是将离散点\(\{\mathbf x_i\}=[x_1,x_2,\cdots,x_n]\)插值成连续函数PDF \(p(\mathbf x)\)。
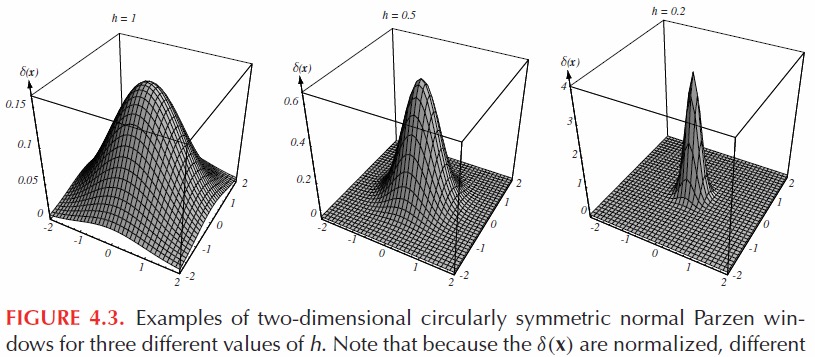
概率神经网络和RBF神经网络几乎等同于Parzen窗口方法。
k最近邻k-NN规则
估计PDF的方法如下
\[\hat p(\mathbf x)=\frac k{nV}\]
Parzen窗口方法选择一个以\(\mathbf x\)为中心、大小固定(体积)\(V\)的区域/单元,并计算该区域/单元中的样本数\(k\),以估计PDF。
我们还可以选择固定数量的样本\(k\),并计算刚好包含\(k\)个样本的大小/体积,以这种方式估计PDF。
这种方法称为k最近邻k-NN估计
两个一维密度的几个k最近邻估计:
\[\hat p(\mathbf x)=\frac k{nV(k)}\]
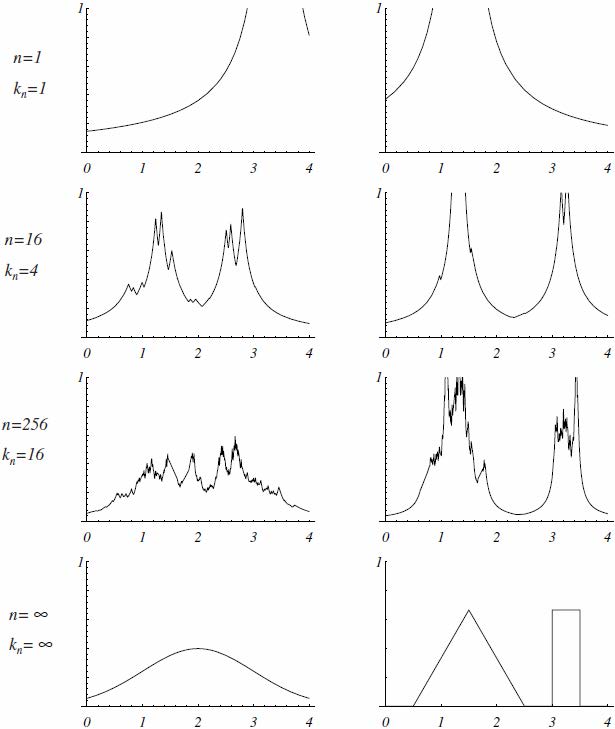
k-NN技术还可用于从一组\(n\)个标记样本中估计后验概率\(P(\omega_i\vert\mathbf x)\)
假设我们在\(\mathbf x\)周围放置一个体积为\(V\)的单元并捕获\(k\)个样本,其中\(k_i\)被标记为\(\omega_i\)。
联合概率的估计值为\(p_n(\mathbf x,\omega_i)=\frac{k_i}{nV}\)
因此,我们可以通过以下方式估计\(P(\omega_i\vert\mathbf x)\):
\[P_n(\omega_i\vert\mathbf x)=\frac{p_n(\mathbf x,\omega_i)}{\sum_{j=1}^cp_n(\mathbf x,\omega_j)}=\frac{k_i}k\]
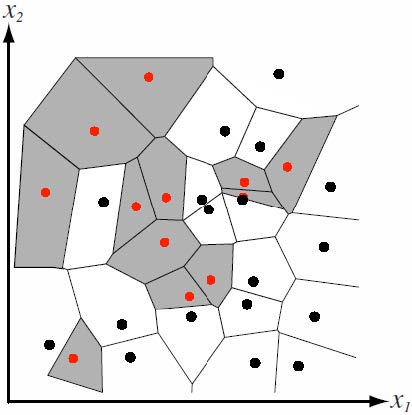
对于大量训练样本,NN 分类器P的错误率被界定为
\[P^*\leq P\leq P^*\left(2-\frac c{c-1}P^*\right)\]

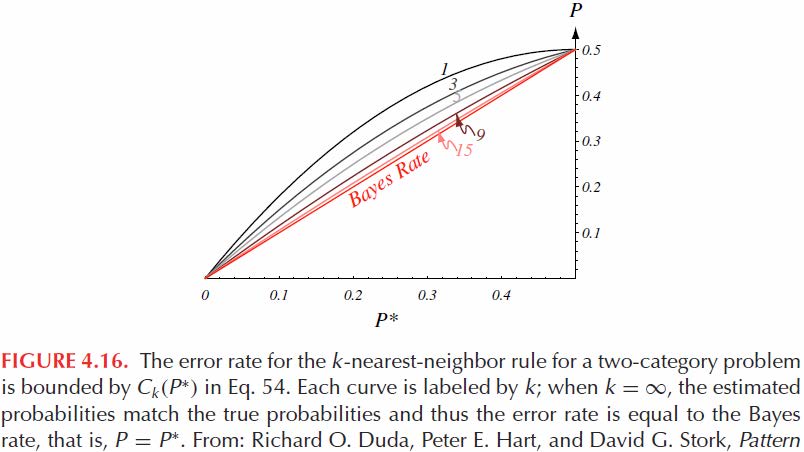
估计概率分布密度的参数方法
我们发现,从训练样本中学习到的条件PDF可能与总体的真实PDF有很大偏差,尤其是在训练样本数量较少的情况下。
如果我们对该问题的一般知识允许我们对条件PDF进行建模,即使用数学解析函数来表示具有未知参数的PDF。这些问题的严重性可以大大降低。在这里,我们将条件PDF参数化,这称为参数化方法。
神经网络和深度学习也是参数方法。
最大似然 (ML) 估计
但我们从最简单的开始。假设\(p(\mathbf x\vert\omega_k)\)是高斯密度,其均值为\(\mu_k\),协方差矩阵为\(\Sigma_k\)。虽然我们不知道它们的值,但这一知识将问题从估计未知函数\(p(\mathbf x\vert\omega_k)\)简化为仅估计未知参数\(\mu_k\)和\(\Sigma_k\)。
现在我们将使用一组独立于概率密度\(p(\mathbf x\vert\theta)\)抽取的训练样本\(D=\{\mathbf x_i\}=[x_1,x_2,\cdots,x_n]\)来估计未知参数向量\(\mathbf\theta\)。
让我们看一个例子来产生如何根据训练数据\(D\)合理地估计给定概率密度\(p(\mathbf x\vert\theta)\)的参数的想法。
该图显示了一维中的几个训练点,已知或假定它们来自特定方差的高斯分布,但均值未知。虚线显示了具有\(4\)个不同均值的四个PDF。
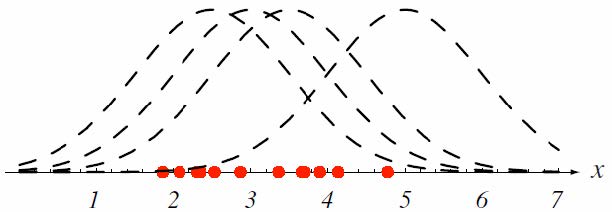
现在我们用数学的方式阐述我们的想法。
显然,样本\(\mathbf x_k\)发生的概率为\(p(\mathbf x_k\vert\theta)\)。由于训练集中所有样本都是独立收集(发生)的,因此所有样本发生的概率为
\[p(D\vert\theta)=\prod_{k=1}^np(\mathbf x_k\vert\theta)\]
直观上,我们应该选择参数,使得概率密度\(p(\mathbf x\vert\theta)\)最好地支持实际观察到的训练样本,即使得所有训练数据发生的概率\(p(D\vert\theta)\)最大。注意,\(p(D\vert\theta)\)称为\(\theta\)关于样本集\(D\)的似然。因此,这种方法称为最大似然(the maximum likelihood,ML)估计。
\[\hat\theta=\argmax_\theta p(D\vert\theta)=\argmax_\theta\prod_{k=1}^np(\mathbf x_k\vert\theta)\]
由于\(\theta\)函数的乘积并且\(p(\mathbf x_k\vert\theta)\)通常是\(\theta\)的非线性函数,因此通常不容易获得解析解。
由于对数是单调递增的,最大化函数的对数也会最大化函数本身。对数具有很好的性质,可以将乘法转换为求和,并简化指数函数。
因此,我们最大化对数似然,而不是最大化似然
\[\hat\theta=\argmax_\theta\ln p(D\vert\theta)=\argmax_\theta\sum_{k=1}^n\ln p(\mathbf x_k\vert\theta)\]
可以通过微积分的标准方法找到解决方案:解梯度为零的方程。
\[\begin{aligned} \nabla_\theta\ln p(D\vert\theta)&=0\\ \nabla_\theta\sum_{k=1}^n\ln p(\mathbf x_k\vert\theta)&=0 \end{aligned}\]
假设需要估计的参数个数为\(q\),则\(\theta\)是一个\(q\)分量向量\(\theta=(\theta_1,\theta_2,\cdots,\theta_q)^\intercal\)。梯度是一个包含针对\(\theta\)所有分量的偏微分的向量。
\[\nabla_\theta f(\theta)\triangleq\left(\begin{array}{c}\frac{\partial f(\theta)}{\partial\theta_1}\\\vdots\\\frac{\partial f(\theta)}{\partial\theta_q}\end{array}\right)\]
多元高斯概率分布密度
为了了解最大似然法结果如何应用于具体情况,假设样本是从具有未知均值\(\mu\)和协方差矩阵\(\Sigma\)的多元高斯总体中抽取的。
\[ p(\mathbf x\vert\theta)=\frac1{(2\pi)^\frac d2\lvert\Sigma\rvert^\frac12}\exp\left[-\frac12(\mathbf x-\mu)^\intercal\Sigma^{-1}(\mathbf x-\mu)\right] \]
单个样本的对数似然为
\[ \ln p(\mathbf x_k\vert\theta)=-\frac12\ln\left[(2\pi)^d\lvert\Sigma\rvert\right]-\frac12(\mathbf x_k-\mu)^\intercal\Sigma^{-1}(\mathbf x_k-\mu) \]
首先考虑单变量情况\(\theta=(\theta_1,\theta_2)^\intercal=(\mu,\sigma^2)^\intercal\)。
\[ p(x\vert\theta)=\frac1{\sqrt{2\pi}\sigma}\exp\left[-\frac12\left(\frac{x-\mu}\sigma\right)^2\right] \]
这里单个样本的对数似然简化为
\[ \ln p(\mathbf x_k\vert\theta)=-\frac12\ln\left[2\pi\sigma^2\right]-\frac1{2\sigma^2}(x_k-\mu)^2 \]
其导数为
\[ \nabla_\theta\ln p(\mathbf x_k\vert\theta)=\begin{pmatrix} \frac1{\sigma^2}(x_k-\mu)\\ -\frac1{2\sigma^2}+\frac{(x_k-\mu)^2}{2\sigma^4} \end{pmatrix} \]
应用ML
\[ \nabla_\theta\ln p(D\vert\theta)=\nabla_\theta\sum_{k=1}^n\ln p(\mathbf x_k\vert\theta)=0 \]
我们有
\[ \begin{cases} \sum_{k=1}^n\frac1{\sigma^2}(x_k-\mu)=0\\ -\sum_{k=1}^n\frac1{2\sigma^2}+\sum_{k=1}^n\frac{(x_k-\mu)^2}{2\sigma^4}=0 \end{cases} \]
解这两个方程,我们得到以下最大似然估计
\[ \begin{cases} \hat\mu=\frac1n\sum_{k=1}^nx_k\\ \hat\sigma^2=\frac1n\sum_{k=1}^n(x_k-\hat\mu)^2 \end{cases} \]
虽然多变量情况的分析基本非常相似,但涉及的操作要多得多。结果是,多元高斯PDF的均值向量\(\mu\)和协方差矩阵\(\Sigma\)的最大似然估计
\[ p(\mathbf x\vert\theta)=\frac1{(2\pi)^\frac d2\lvert\Sigma\rvert^\frac12}\exp\left[-\frac12(\mathbf x-\mu)^\intercal\Sigma^{-1}(\mathbf x-\mu)\right] \]
由下式给出
\[ \begin{cases} \hat\mu=\frac1n\sum_{k=1}^nx_k\\ \hat\sigma^2=\frac1n\sum_{k=1}^n(x_k-\hat\mu)(x_k-\hat\mu)^\intercal \end{cases} \]