分类器性能评估
在监督学习中,分类模型是使用标记数据进行训练的。我们如何了解模型的性能?接下来,我们介绍一些模型评估程序和指标。
评估程序
保留方法
在此方法中,可用数据的一部分/子集被保留下来(这就是“保留”这个名称的由来)用于评估模型。该数据子集用作测试数据,用于评估已训练分类器的性能。
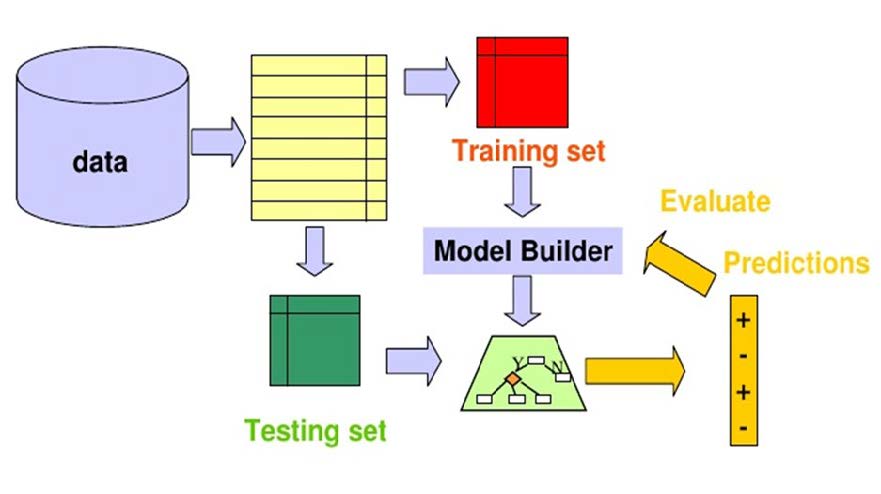
一旦使用训练数据训练了模型,就可以使用训练后的模型预测测试数据的标签。然后将预测值与标签的实际值进行比较。这是可能的,因为测试数据是具有已知标签的可用数据的一部分。模型的性能通过各种指标来衡量,这些指标将在后面介绍。
通常,70%–80%的可用数据(随机抽样)用于分类器训练,剩余的20%–30%用作测试数据。
通常,可用数据分为 3 个部分 - 训练和测试数据以及验证数据。验证数据用于在训练阶段测量模型性能。在通过训练和验证数据确定模型后,测试数据仅使用一次,用于测量和报告模型的最终性能。

该方法的一个明显问题是,不同类别的数据划分为训练数据和测试数据可能不成比例。如果与某些类别相关的数据总体百分比远低于其他类别(即类别不平衡问题),这种情况会更糟。尽管采用随机抽样来选择测试数据,但这种情况仍可能发生。
可以通过应用分层随机抽样代替随机抽样在一定程度上解决此问题。在分层随机抽样中,对每个单独的类别进行随机抽样。例如,每个类别中 70% 和 30% 的样本被随机选择为训练数据和测试数据。这确保生成的随机分区具有相等的每个类别的比例。
重复保留法
保留方法的一种特殊变体称为重复保留,通常用于确保所组成的训练和测试数据集的随机性。
在重复保留中,使用多个随机保留来衡量模型性能。最后,取所有性能的平均值。
由于已抽取多个保留,因此训练和测试数据(以及验证数据,如果已抽取)更有可能包含来自所有类别的代表性数据,并且与原始输入数据非常相似。
K折交叉验证方法
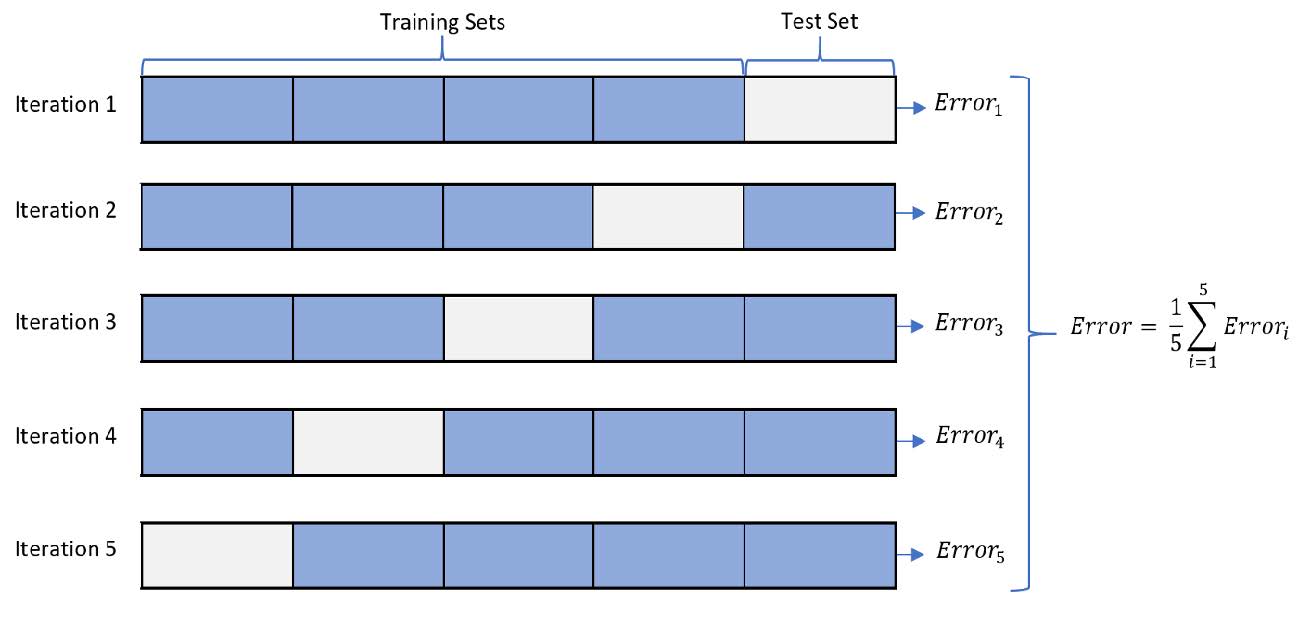
重复保留的过程是k折交叉验证技术的基础。k折交叉验证中,数据集被分成k个完全不同或不重叠的随机分区,称为折叠。
每个\(k\)折叠都有机会用作保留测试集,而所有其他折叠则集体用作训练数据集。在\(k\)保留测试集上共拟合和评估了\(k\)个模型,平均性能报告如下图所示。
留一交叉验证 (LOOCV)
\(k\)折交叉验证的一个极端情况是设置\(k=N\),即样本总数。在这种极端情况下,在每一折中,只有一个样本用作测试数据,其余\(N-1\)个样本用作训练数据。这种极端情况称为留一交叉验证。
这样做是为了最大化用于训练模型的数据数量。很明显,它必须运行的迭代次数(即倍数)等于数据集中的样本总数。因此,它在计算上非常昂贵,并且仅在样本数量较少时使用。
重复K折交叉验证
通过K折交叉验证估计模型性能可能会很嘈杂。这意味着每次运行该过程时,都会使用不同的数据集拆分为\(k\)折,从而获得不同的模型性能平均估计值。从一次K折交叉验证运行到另一次运行的估计性能差异量取决于训练测试数据划分的差异。
解决该问题的方法之一是多次重复K折交叉验证过程,并报告所有倍数和所有重复的平均性能。这种方法通常称为重复K折交叉验证。
绩效评估指标
对于二分类问题,我们假设一个类是正类,另一个是负类。通常,我们感兴趣的类被命名为正类,例如,“癌症”被命名为正类,而“正常”被命名为负类。样本的分类结果可能有四种情况:
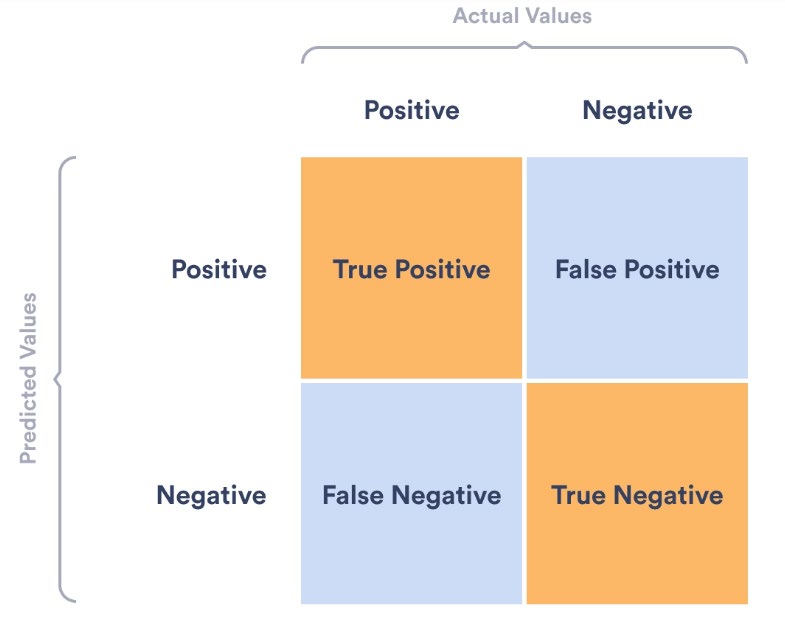
- 真阳性(TP):正类样本被正确分类为正类
- 假阳性(FP):负类样本被错误分类为正类
- 真阴性(TN):负类样本被正确分类为负类
- 假阴性(FN):正类样本被错误分类为负类
混淆矩阵
混淆矩阵是分类结果的总结,如下所示:
准确率
准确率是正确分类的样本的比例:
\[ \text{Acc}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}} \]
错误率
错误率是错误分类的样本所占的比例:
\[ \text{Err}=\frac{\text{FP}+\text{FN}}{\text{TP}+\text{TN}+\text{FP}+\text{FN}} \]
灵敏度和特异性
分类器的灵敏度衡量被正确分类的正样本的比例。其测量方法如下:
\[ \text{Sensitivity}=\frac{\text{TP}}{\text{TP}+\text{FN}} \]
分类器的特异性衡量被正确分类的负样本的比例。其测量方法如下:
\[ \text{Specificity}=\frac{\text{TN}}{\text{TN}+\text{FP}} \]
精确率和召回率
精确率表示的是真正为正的预测所占的比例:
\[ \text{Precision}=\frac{\text{TP}}{\text{TP}+\text{FP}} \]
召回率衡量的是正确预测的正结果占正结果总数的比例:
\[ \text{Recall}=\frac{\text{TP}}{\text{TP}+\text{FN}} \]
F分数
F分数是分类器性能的衡量标准,它结合了精确度和召回率:
\[ \text F=\frac{2\times\text{Precision}\times\text{Recall}}{\text{Precision}+\text{Recall}} \]
接收者操作特征 (ROC) 曲线
在分类问题中,我们使用判别函数来决定样本属于哪个类。在贝叶斯决策规则中,这个判别函数是后验概率。对于二分类问题:
\[ \begin{aligned} \text{Decide }&\omega_1\text{ if }P(\omega_1\vert x)\gt P(\omega_2\vert x)\\ \text{Decide }&\omega_2\text{ if }P(\omega_2\vert x)\gt P(\omega_1\vert x) \end{aligned} \]
在这个决策规则中,我们隐式地假设阈值为0.5。如果属于某个类别的后验概率高于0.5,则样本被分配到该类别。但在某些应用中,例如将患者诊断为“癌症”或“正常”,使用不同的阈值(而不是0.5)可能是更谨慎的选择。
设置不同的阈值来对正类进行分类将不可避免地改变混淆矩阵中的4个指标:TP、FP、TN、FN,从而改变分类模型的其他评估指标。其中一个阈值可能会比其他阈值产生更好的结果,这取决于我们的目标是降低假阴性还是假阳性的数量。
我们可以生成不同的混淆矩阵并比较各种指标。但这样做并不明智。相反,我们可以做的是绘制其中一些指标之间的图,以便我们可以轻松地看到哪个阈值可以给我们带来更好的结果。
ROC曲线正好解决了这个问题。
接收者操作特性 (ROC) 可视化分类模型在检测真阳性同时避免出现假阳性的效率。
我们定义以下措施:
- 真阳性率(TPR):\(\text{TPR}=\frac{\text{TP}}{\text{TP}+\text{FN}}=\text{Recall}=\text{Sensitivity}\)
- 假阳性率(FPR):\(\text{FPR}=\frac{\text{FP}}{\text{FP}+\text{TN}}=1-\text{Specificity}\)
在 ROC 曲线中,在不同分类阈值下绘制了假阳性率(横轴)与真阳性率(纵轴)。
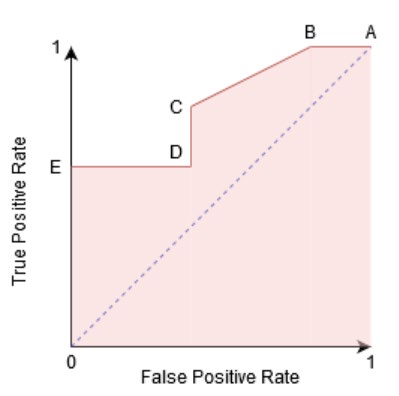
曲线下面积(AUC),即上图中的阴影部分,是衡量分类器区分类别能力的指标。
- 当AUC=1时,分类器能够完美地区分所有正类和负类点;
- 当AUC=0时,分类器会将所有负类预测为正类,将所有正类预测为负类。
- 当AUC=0.5时,分类器无法区分正类和负类点,这意味着分类器预测的是随机类。
- 当0.5<AUC<1时,分类器很有可能能够区分正类和负类,这意味着分类器能够检测到的真阳性和真阴性的数量多于假阴性和假阳性的数量。