降维和分类的特征选择
介绍
在前面的部分中,我们在分类器的设计中使用了所有可用的特征。与模式识别相关的一个问题是所谓的维数灾难,它指的是处理高维数据时出现的问题。数据集的维度对应于数据集中存在的特征数量。由于高维数据而导致的与训练机器学习模型相关的困难被称为“维数灾难”。维数灾难的主要方面是数据稀疏性和距离集中。
将特征数量减少到足够小的原因不止一个。计算复杂性是显而易见的。另一个主要原因是分类器的泛化能力。通常,训练样本数量与自由分类器参数数量之比越高,所得分类器的泛化性能就越好。
大量的特征直接转化为大量的分类器参数(例如神经网络中的突触权重,线性分类器中的权重)。因此,对于有限且通常有限数量的训练样本,保持特征数量尽可能少符合我们设计具有良好泛化能力的分类器的愿望。
此部分的主要任务现可概括如下:
给定若干个特征,如何选出最重要的特征,以减少其数量,同时尽可能多地保留其类别区分信息?
这个问题被称为特征选择或特征减少。
这一步非常关键。如果我们选择的特征辨别能力较弱,那么分类器的后续设计将导致性能不佳。另一方面,如果选择信息丰富的特征,分类器的性能将很好。
必须指出的是,文献中关于特征选择和特征提取的术语存在一些混淆。
简单来说,特征选择就是从原始特征中选取一个特征子集,以降低模型复杂度,提高模型的计算效率,提高泛化能力。
特征提取是从原始特征集中提取或导出信息以创建新的特征子空间。特征提取背后的主要思想是压缩数据,以保留大部分相关信息。常用的主成分分析 (PCA) 是一种特征提取方法。
峰值现象
如上所述,为了设计具有良好泛化性能的分类器,训练样本的数量\(N\)必须相对于特征的数量\(l\)(即特征空间的维数)足够大。以设计线性分类器的情况为例:
\[y=\mathbf w^\intercal\mathbf x+w_0\]
未知参数的数量为\(l+1\)。为了对这些参数进行良好的估计,样本数量\(N\)必须大于\(l+1\)。\(N\)越大,估计效果越好,因为我们可以滤除噪声的影响,同时最小化异常值的影响。
实际上,对于有限的\(N\),通过增加特征数量,可以获得性能的初始改进,但在临界值之后,进一步增加特征数量会导致错误概率增加。这种现象称为峰值现象,如下所示:
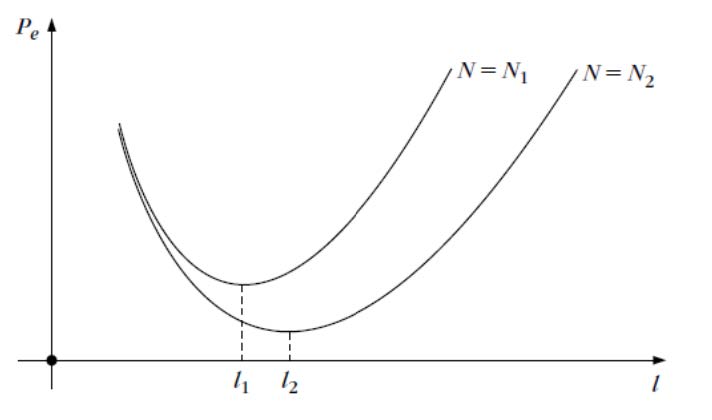
上图说明了通过使用特征数量\(l\)和训练数据集的大小\(N\),人们期望在实践中体验到的总体趋势。
- 对于\(N_2\gg N_1\),\(N_2\)对应的误差值低于\(N_1\)产生的误差值,并且当\(l_2\gg l_1\)时会出现峰值现象。
- 对于\(N\)的每个值,随着\(l\)的增加,误差概率开始减小,直到误差开始增大的临界值。
因此,在实际应用中,如果训练数据较少,则必须使用较少的特征。如果训练数据较多,则可以使用较多的特征以获得更好的性能。
个别特征评估
特征选择的第一步是单独或分开查看每个特征,并测试它们对当前问题的单独判别能力。尽管单独查看特征远非最佳方法,但此过程有助于我们识别和丢弃“坏”特征。这将减轻稍后将介绍的基于集合的特征评估和选择不必要的计算负担。
在这里,我们将介绍两种单独的特征评估方法,基于对良好特征的两种不同解释,包括类可分离性和特征的相关性。
费舍尔比率
如前所述,好的特征应该在不同的类别中采取不同的值。
特征的类可分性可以用Fisher比率来评估。假设两个类中样本的平均值和标准差分别为\(m_1\)、\(\sigma_1\)、\(m_2\)和\(\sigma_1\),则 Fisher 比率定义为:
\[ R=\frac{(m_1-m_2)^2}{\sigma_1^2+\sigma_2^2} \]
费舍尔比率的分子其实就是类间(或称类间)差异,分母则是类内(或称类内)散度。
从 Fisher 比率可以看出,一个好的特征应该具有:
- 类间差异大;
- 类内散度或方差小。
费舍尔比率越大,特征的判别性越强。费舍尔比率通常用于连续变量。
相互信息
一个好的特征应该包含大量信息来决定类标签的值。特征的相关性可以根据特征和类标签之间的互信息来评估。
两个变量的互信息 (MI) 是两个变量之间相互依赖性的度量。更具体地说,它量化了通过观察另一个变量获得的有关一个变量的信息量。
特征\(x\)和类标签\(y\)之间的互信息可以通过以下方式测量:
\[ \text{MI}(x,y)=E(x)+E(y)-E(x,y) \]
其中\(E(x)\)、\(E(y)\)是\(x\)和\(y\)的熵,\(E(x,y)\)是\(x\)和\(y\)的联合熵:
\[ \begin{aligned} E(x)&=-\sum_{u_i\in x}p(x=u_i)\times\log p(x=u_i)\\ E(y)&=-\sum_{c_i\in y}p(y=c_i)\times\log p(y=c_i)\\ E(x,y)&=-\sum_{u_i\in x}\sum_{c_i\in y}p(x=u_i,y=c_i)\times\log p(x=u_i,y=c_i) \end{aligned} \]
其中\(p(x=u_i)\)表示未来\(x\)取\(u_i\)值的概率。互信息通常用于离散特征。
特征子集选择
特征子集选择问题可以定义如下:
给出完整的特征集:
\[ X=\{x_1,x_2,\cdots,x_n\} \]
选择一个子集
\[ Z=\{z_1,z_2,\cdots,z_m\},z_i\in X \]
以产生最佳分类性能。
由于峰值现象,应选择所有可用特征的一个子集并将其用作模式分类模型的输入。上文介绍了对单个特征的评估。是否可以通过简单选择排名靠前的特征来获得特征子集?
答案是否定的。
这是因为排名靠前的特征之间可能存在很强的相关性,这样选择的特征子集可能会表现出严重的冗余。一个好的特征子集应该具有最大的相关性和最小的冗余性。
特征子集选择算法由两个主要部分组成:
- 搜索算法
- 评估标准
搜索算法的目标是生成候选特征子集,而评估标准旨在评估搜索算法生成的候选特征子集的优劣,如下所示
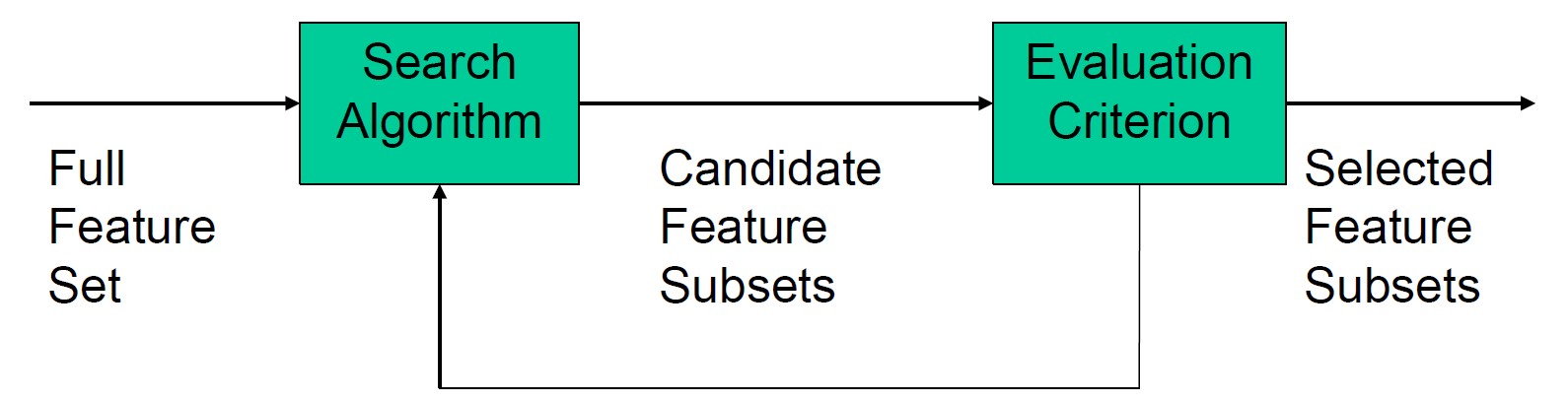
搜索算法
穷举搜索法
顾名思义,穷举搜索将穷举所有可能的子集。换句话说,它会生成\(n\)特征的所有可能组合。
穷举搜索当然不会错过最佳特征子集,但如果\(n\)很大,计算复杂度就会过高。实际上,只有当\(n\)很小时才使用穷举搜索。
顺序前向选择
顺序前向搜索是一种自下而上的方法。它从一个空的特征集开始,逐步添加特征以形成特征子集。在每一步中,根据一定的标准在未选定的特征中选择最佳特征。特征子集不断增长,直到满足停止标准。
顺序后向消除
顺序后向消除法是一种自上而下的方法。它从一组完整的特征开始。每次删除一个特征。每次根据某个标准删除最不重要的特征。特征集不断缩小,直到满足停止标准。
评估标准
为了选择一个好的特征子集,我们需要一种测量特征子集准确区分两个或多个类别的能力的方法。这可以通过定义针对可能的特征子集进行优化的类可分离性度量来实现。
我们可以通过两种方式评估特征子集:
分类器的分类性能
在这个方法中,我们在特征子集上训练一个分类器,然后以分类效果作为评价标准。选择特征子集来匹配分类器。不同的分类器可能会选择不同的特征子集。
可分离性度量
这种方法估计了数据来源分布之间的重叠,并倾向于重叠最小的分布,即最大可分离性。这样选择的特征子集与最终使用的分类器无关。此标准不需要训练大量模式分类器,因此在计算上更高效。
缺点是,估计数据分布重叠时所做的假设通常很粗略,可能与真实分布不太吻合。
接下来,介绍一些可分离性度量。
基于Mahalanobis距离的可分离性测量
可分离性可以通过特征子集空间中两个均值向量之间的Mahalanobis距离来衡量。
对于多类问题,我们可以使用成对可分离性度量的总和
\[ J=\sum_i\sum_{j\ne i}J_{i,j} \]
基于散度的可分离性测量
\[ J=\text{Tr}(\mathbf S_W^{-1}\mathbf S_B) \]
或
\[ J=\frac{\text{Tr}(\mathbf S_B)}{\text{Tr}(\mathbf S_W)} \]
其中\(\mathbf S_B\)和\(\mathbf S_W\)分别为类间和类内散度矩阵。\(\text{Tr}(\mathbf A)\)表示矩阵\(\mathbf A\)的迹,定义为\(\mathbf A\)主对角线上元素之和。
特征子集选择算法
特征子集选择算法由搜索算法和特征子集评价标准组成。根据所使用的评价标准,特征选择算法通常分为三类:过滤方法、包装方法和嵌入式方法。
包装方法在循环中包含一个分类器,并使用分类性能(例如准确率或错误率)作为特征子集评价标准。
过滤方法在循环中不包含分类器,而是采用类可分离性度量作为特征子集评价标准。
包装方法
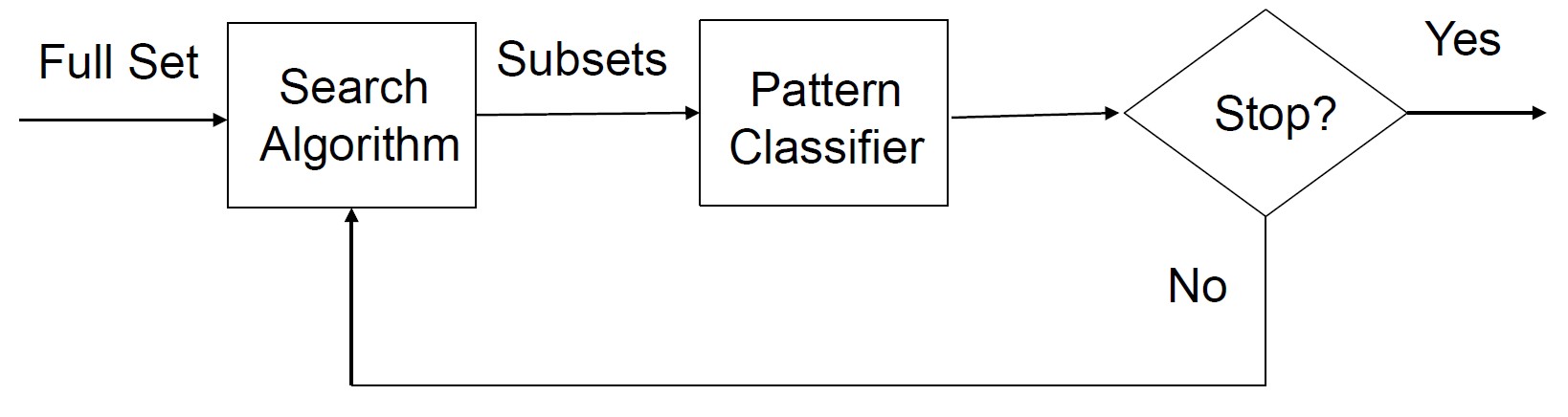
停止标准可以是
- 已达到要选择的特征数量,或
- 分类准确率(在验证集上)达到最佳,或
- 其他
过滤方法

- 已达到要选择的特征数量,或
- 可分离性度量不再提高,或
- 其他
顺序前向特征选择算法
接下来,我们结合顺序前向搜索和评估标准来形成特征选择算法。
- 将每个特征视为候选特征 \(F^{(i)}=\{x_i\}\) 评估可分离性度量(过滤器) \(J^{F(i)}=\frac{\text{Tr}(\mathbf S_B^{F(i)})}{\text{Tr}(\mathbf S_W^{F(i)})}\) 或者训练分类器并找到分类准确率(包装器) \(C^{F(i)}=\text{Classifier Trained on } F(i)\) \(J^{F(i)}=\text{Accuracy}(C^{F(i)})\) 选择具有最大可分离性(过滤方法)或最佳分类性能(包装器方法)的特征作为第一个特征: \(k=\arg\max J^{F(i)}\) \(z_1=x_k\)
- 将剩余的\(n-1\)个特征中的每一个视为第二个特征的候选, \(F^{(i)}=\{z_1,x_i\},i\ne k\) 评估可分离性度量(过滤方法): \(J^{F(i)}=\frac{\text{Tr}(\mathbf S_B^{F(i)})}{\text{Tr}(\mathbf S_W^{F(i)})}\) 或者训练分类器并找到分类准确率(包装方法) \(C^{F(i)}=\text{Classifier Trained on } F(i)\) \(J^{F(i)}=\text{Accuracy}(C^{F(i)})\) 选择达到最大可分离性(过滤方法)或最佳分类性能(包装方法)的特征作为第二个特征。
- 选择过程持续进行,直到满足停止标准
顺序后向特征消除算法
- 将每个特征视为要消除的候选特征, \(F^{(i)}=\{x_1,x_2,\cdots,x_n\}-x_i\) 评估相应的可分离性度量(过滤器) \(J^{F(i)}=\frac{\text{Tr}(\mathbf S_B^{F(i)})}{\text{Tr}(\mathbf S_W^{F(i)})}\) 或者训练一个分类器并找到相应的分类准确率(包装器) \(C^{F(i)}=\text{Classifier Trained on } F(i)\) \(J^{F(i)}=\text{Accuracy}(C^{F(i)})\) 找出对可分离性度量(过滤方法)或分类性能(包装方法)影响最小的特征,并将其作为第一个要删除的特征。
- 消除过程持续进行,直到满足停止标准。
嵌入方法
嵌入式方法结合了过滤器和包装器方法的特性。它由具有内置特征选择方法的算法实现。这种方法最流行的例子是 Lasso(最小绝对收缩和选择运算符,L1正则化),它具有内置机制,通过将与最不重要的特征相关的系数收缩为零来惩罚模型中的特征数量(参见第 8 章)。
\[ \begin{aligned} J_{\text{Lasso}}(\Theta)&=\frac12\left\{\sum_{i=1}^N(\hat y_i-y_i)^2+\lambda\sum_{j=0}^m\lvert\theta_j\rvert\right\}\\ &=\frac12\{(\mathbf y-\Phi\Theta)^\intercal(\mathbf y-\Phi\Theta)+\lambda\lVert\Theta\rVert\} \end{aligned} \]